Висновок

У якості апроксимуючої кривої для функції цінності вибираємо логарифмічну, бо по-перше для квадратичної функції не виконуються умови нормування , ( ), а по-друге точність апроксимації у логарифмічної кривої вища за точність квадратичної кривої ( ). Рівняння найкращої апроксимуючої функції для функції корисності має вигляд: .

Лабораторна робота №4

Тема: Побудова та апроксимація функції корисності на одновимірній множині

Для виконання лабораторної роботи №4 студент повинний знати:

• мету і зміст даної роботи, порядок її виконання;

• знаходження вихідних даних за методом половинного поділу поточного проміжку за корисністю;

• виведення системи для отримання параметрів апроксимуючої функції при лінійній, квадратичній та логарифмічній залежностях;

• метод найменших квадратів побудови апроксимуючої функції;

Студент повинний уміти:

1. Працювати з масивами даних;

2. Будувати електронні таблиці;

3. працювати з графіками в оболонці електронних таблиць Excel.

4. оцінювати схильність/несхильність до ризику, використовуючи коефіцієнт Пратта-Ерроу .

Студент повинний підготувати:

Алгоритм знаходження апроксимуючої функції з використанням електронних таблиць.

Завдання.

Зауваження: Дана лабораторна робота виконується двома студентами, що мають варіанти відповідно , , .

Заданий проміжок [10;N₁+20] та відповідні значення функції корисності , , , , .

Перший етап. Кожному студентові скласти таблицю значень прибутку та відповідних їм корисностей наслідків, виходячи із власної системи переважань, використовуючи метод половинного поділу поточного проміжку за корисністю.

Другий етап.

1. Апроксимувати функцію корисності за допомогою:

а) лінійної,

б) квадратичної,

в) кубічної,

г) логарифмічної,

або будь-якої іншої функції.

2. Визначити, яка з побудованих функцій найкращим чином апроксимує функцію , використовуючи коефіцієнт детермінації R².

Третій етап.

1. Знайти коефіцієнти Пратта-Ерроу для всіх одержаних на другому етапі апроксимуючих функцій, які не мають точок перегину на [10;N₁+20].

2. Використовуючи функцію корисності, знайдену у п.2 другого етапу та відповідний коефіцієнт Пратта-Ерроу

а) визначити, чи схильний кожен зі студентів до ризику;

б) у випадку, коли обидва студенти мають схильність або несхильність до ризику, визначити, хто має “більшу”.

Приклад виконання роботи: Тендерна комісія оцінює схильність до ризику двох інвесторів А та В у справі реалізації проекту реорганізації підприємства легкої промисловості. Припускається, що чистий прибуток від інвестицій може бути від 10 до 100 тис грн. Значення функції корисності відповідно , , , , для обох інвесторів.

Розв’язання:

Перший етап. Інвестори відповідно до власної системи переважань розставили пріорітети наступним чином:

, , , , (для інвестора А).

, , , , (для інвестора В).

На проміжках [43,85] та [20,54] інвесторами знайдено точки з : . Так як , , то розбіжність відповідно між , та , для обох інвесторів вважається неістотною. Комісією занесено отримані дані в таблицю (Табл. 1.13).

Таблиця 1.13
Корисність		Прибуток, тис. грн.
		Інвестор А		Інвестор В
(позначення)	(значення)	(позначення)	(значення)	(позначення)	(значення)
	0		10		10
	0,25		43		20
	0,5		70		33
	0,75		85		54
	1		100		100

Другий етап. (Побудова та апроксимація функцій корисності інвесторів А та В.)

Для роботи використаємо пакет Excel. Опишемо порядок виконання роботи:

По перше вихідні дані запишемо в робочу таблицю в блок (A1:С5).

По друге по введеним у робочу таблицю будуємо діаграму. Оскільки необхідно будувати динаміку змін цінності в залежності від прибутку, то будемо будувати діаграму “Точечная”. Для цього кліком курсору миші на панелі інструментів викликаємо “Мастер диаграмм”. В діалоговому вікні вибираємо тип діаграми “Точечная”. Вигляд – лівий верхній. Натискаємо “Далее” і вказуємо діапазон значень Y: A1:A5 (за допомогою миші). Перевіряємо положення перемикача Ряды: в столбцах. Вибираємо вкладку Ряд та за допомогою миші вводимо діапазон значень Х: B1:B5. На цій же вкладці натискаємо кнопку “Добавить”. Отримали Ряд 2, для якого повторимо вищевказану процедуру вводу даних, вказавши діапазон значень Х: С1:С5. Вводимо назви діаграми, осей Х та Y. Отримано графіки експериментальних даних.

По третє здійснимо апроксимацію отриманих кривих. Курсор миші встановлюємо на одну з точок одного з графіків та натискаємо праву кнопку. У виниклому контекстному меню вибираємо “Добавить линию тренда”. З’являється діалогове вікно Линия тренда. В залежності від вигляду кривої вибираємо відповідний тип лінії тренду. Відкриваємо вкладку “Параметры” та встановлюємо мітки в поля показывать уравнение не диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Натискаємо кнопку ОК. Аналогічну процедуру повторимо для другої кривої. Отримали найкращі апроксимуючі криві (Див. Рис. 1.7): для інвестора А – квадратичну , для інвестора В – логарифмічну .

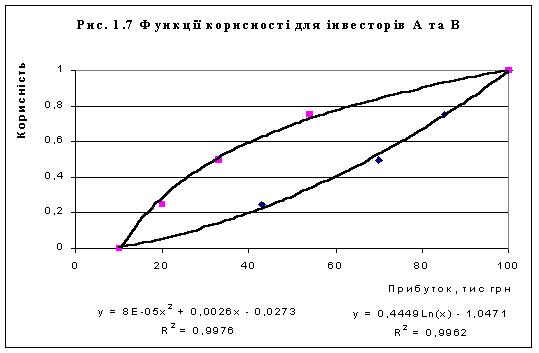
Третій етап. Визначимо схильність до ризику інвесторів А та В:

Візуальний аналіз Рис. 1.7 вказує на схильність інвестора В до ризику та несхильність до ризику інвестора А. Те ж саме виявляє й аналітичний підхід з використанням коефіцієнта Пратта-Ерроу:

,

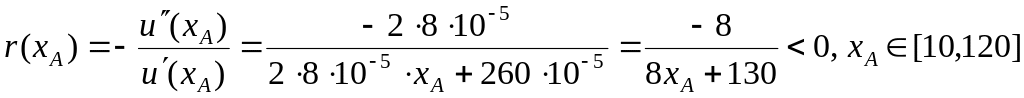отже інвестор А не є схильним до ризику.

,

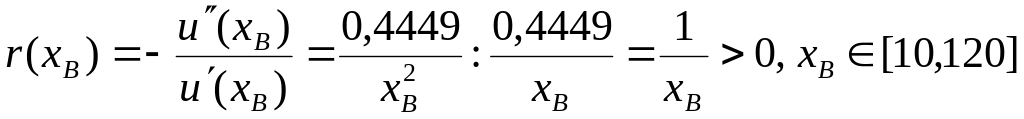отже інвестор В виявляє схильність до ризику.