67

2.12. Локальный экстремум числовой функции нескольких вещественных переменных

В этом параграфе содержится элементарное изложение вопроса о точках локального экстремума числовой функции векторного аргумента. Слово «локальный» (как и в одномерном анализе) означает, что экстремальные свойства имеют место лишь в некоторой окрестности рассматриваемой точки. Если на векторный аргумент в пределах соответствующей окрестности не накладывается никаких дополнительных ограничений, то говорят о безусловном локальном экстремуме. В противном случае, т.е., когда ставится задача об отыскании точки локального экстремума при условии, что аргумент должен удовлетворять определенным ограничениям, заданным в виде системы уравнений, говорят об условном локальном экстремуме.

Безусловный локальный экстремум

Определение 2.24. Точка из области определения функции называется точкой безусловного локального экстремума, если существует такая окрестность точки , что приращение функции при любом не меняет знака.

Соответственно, если это приращение неотрицательно, то точка называется точкой безусловного локального минимума, если же неположительно, то - точкой безусловного локального максимума.

Если указанное приращение строго положительно (отрицательно), то точка называется точкой строгого безусловного локального минимума (максимума).

Впредь, рассматривая безусловный экстремум, будем, как правило, прилагательное «безусловный» опускать.

Докажем сначала простое необходимое условие локального экстремума.

Теорема 2.8. Если функция дифференцируема в точке , и эта точка есть точка локального экстремума функции , то первый дифференциал функции в этой точке обращается в нуль: .

Доказательство. Для дифференцируемой функции ее приращение в точке представимо в виде:

.

По условию найдется такое , что это приращение не меняет знака. Предположим тогда, что при этом . Вектор всегда можно выбрать так, что как точка , так и точка принадлежат той окрестности точки , в которой приращение функции не меняет знака (см рис. 2.15). Но если , то , а так как слагаемое не влияет на знак всего приращения, то приращение функции в рассматриваемой окрестности точки меняет знак. Полученное противоречие и доказывает теорему.

Рис. 2.15

Определение 2.25. Точка называется стационарной точкой функции ( дифференцируемой в ), если .

Из теоремы 2.8 следует, что точка локального экстремума функции является ее стационарной точкой. Обратное, конечно, неверно, что показывает простой пример: точка является стационарной точкой функции , но не является точкой ее локального экстремума (почему?).

Достаточное условие локального экстремума мы докажем в предположении, что исследуемая функция является достаточно гладкой в некоторой окрестности стационарной точки.

Теорема 2.9. Если - стационарная точка функции , для некоторой окрестности точки , и , то - точка строгого локального минимума (максимума) функции .

Доказательство. По теореме 2.7 можно написать:

.

Так как - стационарная точка функции , то , и, следовательно, знак приращения функции в точке определяется знаком ее второго дифференциала в этой точке.

Теорема доказана.

Практически для определения знака второго дифференциала достаточно применить критерий Сильвестра (п. 1.17, теорема 1.18) к матрице Гессе функции в исследуемой точке.

Таким образом, может быть предложена следующая схема исследования функции на локальный экстремум.

1. Найти все стационарные точки функции из условия (или, что равносильно, ).

2. Для каждой стационарной точки выяснить знакоопределенность квадратичной формы второго дифференциала .

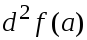3. В тех точках, в которых указанная форма положительно (отрицательно) определена, имеет место строгий локальный минимум (максимум).

4. В тех точках, где квадратичная форма второго дифференциала является формой общего вида, экстремума нет.

5. В тех точках, где форма полуопределена, требуется дополнительное исследование.

Это дополнительное исследование нуждается в комментарии. Рассмотрим пример. Зададим функцию двух переменных

Вычисляя частные производные, получим:

Из условия равенства их нулю будем иметь:

откуда .

Вычислим вторые производные:

Поэтому второй дифференциал в произвольной точке будет равен

Матрица Гессе в точке равна , и

Сразу видно, что второй дифференциал в данной точке положительно полуопределен, причем при он обращается в нуль (это соответствует вектору приращения аргумента ). Следовательно, по направлению, задаваемому этим вектором, приращение функции не может быть вычислено, если ограничиться только вторым дифференциалом. Попробуем тогда найти третий дифференциал нашей функции в этой точке. Имеем: