2) Достаточность. Пусть - изоморфизм. Тогда для каждого существует единственный такой, что .

Введем отображение так, что

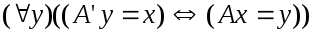
Другими словами, мы определили такое отображение из в , что образ есть тот самый (единственный в силу того, что изоморфизм!) , для которого :

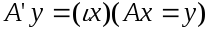
(здесь использовано так называемое «йота-обозначение», или «йота-оператор»:означает «тот единственный , для которого истинно »).

Из определения отображения сразу следует, что

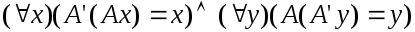
Это значит, что осталось только показать, что отображение линейно.

Имеем: для произвольных пусть , а . Тогда

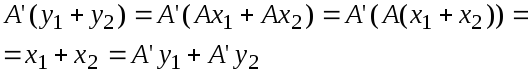
Совершенно аналогично доказывается, что (для любого вещественного ).

Итак, отображение линейно и, следовательно, .

Теорема доказана.

Следствие 1.1 Если - изоморфизм, то - также изоморфизм.

Следствие 1.2 Композиция изоморфизмов есть изоморфизм, причем для изоморфизмов .

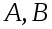
Определение 1.15 Линейные пространства и называются изоморфными, если существует изоморфизм одного из них на другое.

Для изоморфных пространств будем писать . На основании доказанного выше мы можем утверждать:

1. 

2. 

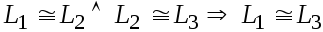
3. Для всякого .

Содержательно тот факт, что два линейных пространства изоморфны, означает, что между этими пространствами можно установить такое взаимно однозначное соответствие , что для любых векторов одного из этих пространств

,

т.е., с точки зрения линейных операций над векторами, эти пространства неразличимы. Тогда, например, если вычисления удобнее выполнять в каком-то одном пространстве, то эти вычисления можно выполнить именно в этом пространстве, а получив результат, «вернуться» в другое пространство.

Оказывается, любое конечномерное линейное пространство совпадает «с точностью до изоморфизма» с арифметическим векторным пространством для подходящего .

Теорема 1.3 Конечномерное линейное пространство , размерность которого изоморфно арифметическому пространству .

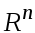Доказательство. Выберем в пространстве какой-то базис и разложим по нему произвольно выбранный вектор :

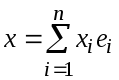
Отображение зададим тогда так:

,

т.е., любому вектору сопоставляется столбец его координат в некотором базисе. Ясно, что относительно фиксированного базиса отображение взаимно однозначно. Линейность его также легко проверяется.

Итак, в силу доказанной теоремы, если отождествлять изоморфные линейные пространства, то любое конечномерное линейное пространство совпадает с пространством арифметических векторов подходящей размерности.

Например, в пространстве матриц система матриц, где ,

образует базис.

Следовательно, .

Заметим еще, что если отождествлять конечномерное линейное пространство с изоморфным ему арифметическим, то исчезает и принципиальное различие между мономорфизмом и изоморфизмом.

Действительно, если мономорфизм рассматривать как изоморфизм на , то при получим цепочку изоморфизмов:

,

что дает нам право считать мономорфизм изоморфизмом арифметического пространства на себя.