25

1.7. Линейные операторы

Определение 1.10 Отображение линейного пространства в линейное пространство называется линейным, если:

1. для любых двух векторов

;

2. для любого вещественного и любого вектора

Равносильное определение линейного отображения: для любых векторов и любых вещественных образ линейной комбинации

Замечание. Рассматривая отображение (функцию) из линейного пространства в линейное пространство , мы часто будем пользоваться обозначением , обозначая образ вектора в пространстве через (без скобок), или (со скобками).

Из определения сразу следует, что образ нулевого вектора при линейном отображении будет нулевым вектором, так как

(Разумеется, здесь, вообще говоря, речь идет о двух разных, хотя и одинаково обозначаемых нулевых векторах: один берется в пространстве , а другой - в ).

Линейное отображение называют также часто линейным оператором. Про линейный оператор будем говорить, что он действует из пространства в пространство . Если , то соответствующий линейный оператор называют линейным преобразованием (пространства ).

Для оператора мы иногда будем говорить, что есть линейный оператор типа .

Примеры. 1) В пространстве всех геометрических векторов определим отображение проектирования на координатную плоскость :

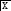
Линейность данного отображения легко проверяется (она может быть доказана и алгебраически, и чисто геометрически - исходя из свойств проекций).

2. В том же пространстве геометрических векторов зададим отображение сдвига на данный вектор : .

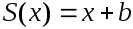Это отображение не является линейным при ненулевом векторе , ибо тогда образ нулевого вектора не будет нулевым вектором. Отображение сдвига при будет тождественным преобразованием пространства , которое, очевидно, линейно.

3. Любая матрица 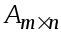определяет линейный оператор, действующий из арифметического пространства в арифметическое пространство : для любого 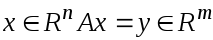. Линейность следует из свойств операций над матрицами.

   4) В пространстве отображение, состоящее в интегрировании функции по данному отрезку, будет линейно в силу свойств линейности определенного интеграла. Заметим, что в данном случае образ

   

   есть функция-константа, значение которой на всем отрезке равно значению указанного интеграла.

5) Рассмотрим множество всех функций, непрерывно дифференцируемых на отрезке (т.е., функций, имеющих на отрезке непрерывную производную) . Нетрудно видеть, что это будет подпространство пространства . Тогда отображение, состоящее в вычислении первой производной функции, будет линейным отображением в (но не будет, конечно, преобразованием пространства , так производная дифференцируемой функции в общем случае не является дифференцируемой).

Определение 1.11 Ядром линейного оператора называется множество всех таких векторов , что .

Ядро оператора обозначается . Таким образом,

Определение 1.12 Образом линейного оператора называется множество всех таких векторов , что существует такой , что .

Образ оператора обозначается . Таким образом,

Итак, ядро линейного оператора - это множество всех векторов, отображаемых в нулевой вектор, а образ линейного оператора - не что иное, как область значений оператора как функции.

Вернемся к приведенным выше примерам.

Ядро оператора проектирования - это множество всех векторов, перпендикулярных координатной плоскости ; образом же этого оператора служат все векторы, параллельные указанной координатной плоскости.

Ядро оператора, задаваемого матрицей, есть множество всех решений однородной линейной системы

,

тогда как образ этого оператора - это множество всех таких векторов , что система

совместна, то есть (в согласии с теоремой Кронекера-Капелли) таких, что

.

Ядро оператора интегрирования - это множество всех таких функций , что . В частности, если , то ядро оператора интегрирования включает в себя множество всех нечетных функций. Образ этого оператора состоит из всех функций, постоянных на отрезке.

Ядром оператора дифференцирования служит множество всех функций-констант. Так как всякая непрерывная функция имеет первообразную, то в данном случае образ линейного оператора совпадает со всем пространством .

Важным является следующее утверждение:

Утверждение 1.6 Ядро линейного оператора есть подпространство пространства , а образ указанного оператора есть подпространство пространства

Доказательство. Если , то , откуда . Далее: , т.е. .

Итак, ядро есть подпространство пространства .

Пусть теперь . Это значит, что найдутся такие , что , но тогда , откуда и следует, что . Аналогично доказывается, что .

Определение 1.13 Линейный оператор называется мономорфизмом пространства в пространство , если для каждого существует единственный такой, что .

Мономорфизм называется изоморфизмом пространства на пространство , если .

Из определения 1.13 и утверждения 1.6 сразу следует, что любой мономорфизм можно рассматривать как изоморфизм на .

Утверждение 1.7 Линейный оператор является мономорфизмом тогда и только тогда, когда .

Доказательство. 1) Необходимость. Если мономорфизм, то из равенства следует, что , так как существует только один вектор, отображаемый в нулевой, а образ нулевого вектора есть нулевой вектор.

2. Достаточность. Пусть ; предположим, что для некоторых . Тогда .

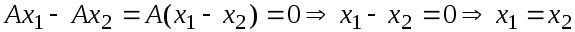Утверждение доказано.

Фундаментальная роль понятия изоморфизма выяснится позже, после обсуждения алгебраических действий над линейными операторами.