1.4. Преобразования базисов

Пусть задан в линейном пространстве некоторый базис. Тогда любой векторможет быть разложен единственным образом по базису (материал первого семестра!):

Введем новый базис . В этом базисе тот же самый векторбудет иметь уже другие координаты:

Возникает задача: связать между собой координаты произвольного вектора в двух различных базисах. Эту задачу будем называть задачей преобразования базисов.

Чтобы технически удобно решить эту задачу и подобные ей, введем в рассмотрение новый объект - векторную матрицу-строку. Это обычная матрица-строка, но ее элементами являются не числа, а векторы (из некоторого линейного пространства). Любую систему векторов можно задать в виде векторной матрицы строки.

Для векторной матрицы-строки определим умножение ее справа на обычную числовую матрицуразмерадля данного, равного числу векторов строки и произвольногоследующим образом:

Таким образом, по определению, результатом умножения векторной матрицы строки справа на числовую матрицу будет новая векторная матрица-строка, число компонент которой равно числу столбцов матрицы , и каждая компонента вычисляется как умножение векторной строки на соответствующий столбец числовой матрицы по тому же правилу, что и в обычном матричном умножении, но только вместо числового умножения используется умножение вектора на число.

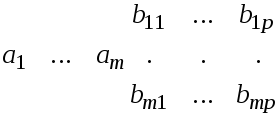
Легко доказать (по аналогии с доказательством ассоциативности умножения числовых матриц) следующее равенство:

(каковы бы ни были числовые матрицы и, произведение которых существует).

С использованием векторных матриц-строк удобно записывать разложение произвольных систем векторов по данному базису.

Пусть дан базис (в виде векторной матрицы-строки) и система векторов. Запишем разложение векторов системыпо базису:

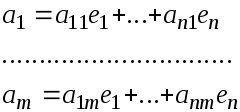
Или, с использованием векторных матриц-строк:

Нетрудно сообразить, что j-ый столбец матрицы - это столбец координат векторав базисе.

Утверждение 1.3 Если система линейно независима, то столбцы матрицылинейно независимы.

Доказательство. Предположим противное - тогда найдутся числа , не все равные нулю, такие, что

,

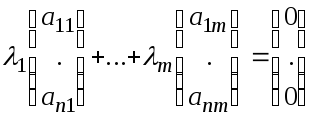или, покомпонентно:

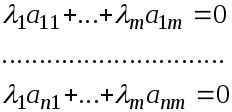
С учетом этих равенств рассмотрим линейную комбинацию

Подставляя вместо каждого вектора , его разложение по базису, получим:

Итак, мы получили нетривиальную линейную комбинацию линейно независимых векторов, равную нулю, что невозможно.

Можно заметить, что, проводя рассуждения доказательства утверждения 1.3 в обратном порядке, получим, что верно и обратное: если столбцы матрицы линейно независимы, то система векторовлинейно независима. Следовательно, для распознавания линейной независимости произвольной системы векторов конечномерного линейного пространства достаточно составить матрицу из столбцов координат векторов системы в произвольном фиксированном базисе и доказать линейную независимость этих столбцов, используя, например, метод элементарных преобразований (т.е., вычислив ранг составленной матрицы).

Для одного вектора его разложение по базису задается в виде:

, где - столбец координат векторав базисе.

Вернемся к задаче преобразования базисов. Запишем разложение нового («штрихованного») базиса в старом (не «штрихованном»):

Матрица (квадратная порядка) называетсяматрицей перехода от базиса к базису. Каждый ее столбец есть, как мы только что доказали, столбец координат соответствующего вектора нового базиса в старом базисе. В силу утверждения 1.3 столбцы матрицылинейно независимы, тем самым ее ранг равен, и матрицаявляется невырожденной.

Тогда для разложения вектора в новом базисе получим:

Отсюда по теореме о единственности разложения вектора по базису (первый семестр!)

Так как матрица не вырождена, то

Итак, чтобы вычислить столбец координат вектора в новом базисе, достаточно матрицу, обратную к матрице перехода, умножить на столбец координат вектора в старом базисе.

По контрасту заметим, что для того, чтобы получить сам новый базис (как векторную матрицу-строку), нужно старый базис умножить на саму матрицу перехода.

Таким образом, можно заметить, что сами базисы и координаты векторов в базисах при переходе от базиса к базису перевычисляются «зеркально» по отношению к друг другу.

Утверждение 1.4 1) Если - матрица перехода от базисак базису, то обратная матрицаявляется матрицей перехода от базисак базису.

2. Если - матрица перехода от базисак базису, а- матрица перехода от базисак базису, то- матрица перехода от базисак базису.

Схематически:

Т T S

T^{- -1}

TS

Доказательство. Упражнение.

Со сложными преобразованиями базисов связана следующая задача: пусть векторы базисов изаданы своими координатами в некотором базисе(который сам может быть явно и не определен). Требуется найти матрицуперехода отк.

Составляем матрицы перехода от ки отк(по столбцам координат векторов базисови). Пусть это будут матрицыисоответственно. Тогда используя утверждение 1.4, легко получим (см. рис. 1.2):

A B

T

рис. 1.2

1В приведенном доказательстве нулевой вектор обозначен как0.