
02 семестр / Разное / Теория по линейной алгебре (определения, доказательства, формулы) / V782RhwLleN / Linal / LINALG4
.DOC
1.9. Матрица линейного оператора
Пусть
![]() - линейный оператор, причем пространства
- линейный оператор, причем пространства
![]() и
и
![]() конечномерные, и
конечномерные, и
![]() .
.
Зададим произвольно базисы:
![]() в
в
![]() и
и
![]() в
в
![]() .
.
Поставим задачу: для произвольного
вектора
![]() вычислить координаты вектора
вычислить координаты вектора
![]() в базисе
в базисе
![]() .
.
Имеем:
![]() ,
,
![]() .
.
Вводя векторную матрицу-строку
![]() ,
состоящую из образов векторов базиса
,
состоящую из образов векторов базиса
![]() ,
получим:
,
получим:
![]()
Заметим, что последнее в этой цепочке
равенство имеет место как раз в силу
линейности оператора
![]() .
.
Разложим систему векторов
![]() по базису
по базису
![]() :
:
![]() ,
,
где
![]() -
ый столбец матрицы
-
ый столбец матрицы
![]() есть столбец координат вектора
есть столбец координат вектора
![]() в
базисе
в
базисе
![]() .
.
Окончательно будем иметь:
![]()
Итак, для того, чтобы вычислить
столбец координат вектора
![]() в выбранном базисе второго пространства,
достаточно умножить столбец координат
вектора
в выбранном базисе второго пространства,
достаточно умножить столбец координат
вектора
![]() в выбранном базисе первого пространства
слева на матрицу, состоящую из столбцов
координат образов базисных векторов
первого пространства в базисе второго
пространства.
в выбранном базисе первого пространства
слева на матрицу, состоящую из столбцов
координат образов базисных векторов
первого пространства в базисе второго
пространства.
Матрица
![]() называется матрицей линейного оператора
называется матрицей линейного оператора
![]() в
заданной паре базисов
в
заданной паре базисов
![]() .
.
Матрицу линейного оператора условимся
обозначать той же буквой, что и сам
оператор, но без курсива. Иногда
будем использовать и такое обозначение:
![]() ,
опуская зачастую ссылки на базисы (если
это не вредит точности).
,
опуская зачастую ссылки на базисы (если
это не вредит точности).
Для линейного преобразования (т.е., когда
![]() ) можно говорить о его матрице в данном
базисе.
) можно говорить о его матрице в данном
базисе.
В качестве примера рассмотрим матрицу
оператора проектирования из примера
п. 1.7 (считая его преобразованием
пространства
![]() геометрических
векторов). В качестве базиса выберем
обычный базис
геометрических
векторов). В качестве базиса выберем
обычный базис
![]() .
.
Имеем:
![]()
Следовательно, матрица оператора
проектирования на плоскость
![]() в базисе
в базисе![]() имеет вид:
имеет вид:

Заметим, что если бы мы рассматривали
оператор проектирования как отображение
![]() в
в
![]() ,
понимая под последним пространство
всех геометрических векторов, лежащих
в плоскости
,
понимая под последним пространство
всех геометрических векторов, лежащих
в плоскости
![]() ,
то, беря в качестве базиса
,
то, беря в качестве базиса
![]() базис
базис
![]() ,
получим уже такую матрицу:
,
получим уже такую матрицу:

Рассматривая произвольную матрицу
размера
![]() как линейный оператор, отображающий
арифметическое пространство
как линейный оператор, отображающий
арифметическое пространство
![]() в арифметическое пространство
в арифметическое пространство
![]() ,
и выбирая в каждом из этих пространств
канонический базис, получим, что матрица
данного линейного оператора в такой
паре базисов есть та самая матрица,
которая определяет данный оператор -
то есть, в данном случае матрица и
линейный оператор есть одно и то же
(точно так же, как при выборе канонического
базиса в арифметическом векторном
пространстве вектор и столбец его
координат в данном базисе можно
отождествить). Но было бы грубой ошибкой
отождествлять вектор как таковой
и линейный оператор как таковой
с их представлением в том или ином
базисе (в виде столбца или матрицы). И
вектор, и линейный оператор суть
геометрические, инвариантные объекты,
определяемые независимо от какого-либо
базиса. Так, когда мы, например, рисуем
геометрический вектор как направленный
отрезок, то он определен совершенно
инвариантно, т.е. нам, когда мы его рисуем,
нет никакого дела до базисов, систем
координат и т. п., и мы можем им оперировать
чисто геометрически. Другое дело, что
для удобства этого оперирования,
для удобства вычислений с векторами,
мы строим определенный алгебраический
аппарат, вводя системы координат, базисы
и связанную с ними чисто алгебраическую
технику вычислений над векторами.
Образно говоря, вектор, как «голый»
геометрический объект, «одевается» в
различные координатные представления
в зависимости от выбора базиса. Но
человек может надеть на себя самое
разнообразное платье, от чего его суть
как человека не меняется, но верно и то,
что не любое платье подходит к той или
иной ситуации (на пляж не пойдешь в
концертном фраке), да и голым тоже не
везде пройдешься. Так и не любой базис
годится для решения данной задачи, равно
как и чисто геометрическое решение
может оказаться слишком сложным. Мы
увидим в нашем курсе, как для решения
такой, казалось бы, чисто геометрической
задачи, как классификация поверхностей
второго порядка, строится довольно
сложная и красивая алгебраическая
теория.
,
и выбирая в каждом из этих пространств
канонический базис, получим, что матрица
данного линейного оператора в такой
паре базисов есть та самая матрица,
которая определяет данный оператор -
то есть, в данном случае матрица и
линейный оператор есть одно и то же
(точно так же, как при выборе канонического
базиса в арифметическом векторном
пространстве вектор и столбец его
координат в данном базисе можно
отождествить). Но было бы грубой ошибкой
отождествлять вектор как таковой
и линейный оператор как таковой
с их представлением в том или ином
базисе (в виде столбца или матрицы). И
вектор, и линейный оператор суть
геометрические, инвариантные объекты,
определяемые независимо от какого-либо
базиса. Так, когда мы, например, рисуем
геометрический вектор как направленный
отрезок, то он определен совершенно
инвариантно, т.е. нам, когда мы его рисуем,
нет никакого дела до базисов, систем
координат и т. п., и мы можем им оперировать
чисто геометрически. Другое дело, что
для удобства этого оперирования,
для удобства вычислений с векторами,
мы строим определенный алгебраический
аппарат, вводя системы координат, базисы
и связанную с ними чисто алгебраическую
технику вычислений над векторами.
Образно говоря, вектор, как «голый»
геометрический объект, «одевается» в
различные координатные представления
в зависимости от выбора базиса. Но
человек может надеть на себя самое
разнообразное платье, от чего его суть
как человека не меняется, но верно и то,
что не любое платье подходит к той или
иной ситуации (на пляж не пойдешь в
концертном фраке), да и голым тоже не
везде пройдешься. Так и не любой базис
годится для решения данной задачи, равно
как и чисто геометрическое решение
может оказаться слишком сложным. Мы
увидим в нашем курсе, как для решения
такой, казалось бы, чисто геометрической
задачи, как классификация поверхностей
второго порядка, строится довольно
сложная и красивая алгебраическая
теория.
Понимание отличия геометрического
объекта от его представления в том или
ином базисе составляет основу восприятия
линейной алгебры. И геометрическим
объектом вовсе не обязан быть именно
геометрический вектор. Так, если мы
зададим арифметический вектор
![]() , то его можно отождествить со столбцом
его координат в каноническом базисе
, то его можно отождествить со столбцом
его координат в каноническом базисе
![]() ,
ибо (см. первый семестр):
,
ибо (см. первый семестр):
![]() .
.
Но введем другой базис в
![]() ,
состоящий из векторов
,
состоящий из векторов
![]() и
и
![]() (проверьте, что это действительно базис!)
и, используя матрицу перехода
(проверьте, что это действительно базис!)
и, используя матрицу перехода
![]() ,
пересчитаем координаты нашего вектора:
,
пересчитаем координаты нашего вектора:

Мы получили совсем другой столбец, но он представляет в другом базисе тот же самый арифметический вектор.
Сказанное о векторах приложимо и к линейным операторам. То, чем для вектора является его координатное представление, тем для линейного оператора является его матрица.
Итак (повторим еще раз), нужно четко разграничивать сами по себе инвариантные, геометрические, объекты, каковы вектор и линейный оператор, и их представление в том или ином базисе (речь, разумеется, идет о конечномерных линейных пространствах).
Займемся теперь как раз задачей преобразования матрицы линейного оператора при переходе от одной пары базисов к другой.
Пусть
![]() - новая пара базисов в
- новая пара базисов в
![]() и
и![]() соответственно.
соответственно.
Тогда (обозначая
![]() матрицу оператора
матрицу оператора
![]() в
паре «штрихованных» базисов) получим:
в
паре «штрихованных» базисов) получим:
![]()
Но, с другой стороны,
![]() ,
,
откуда, в силу единственности разложения вектора по базису
![]() ,
,
или
![]()
Для линейного преобразования формула принимает более простой вид:
![]()
Матрицы
![]() и
и
![]() ,
связанные таким соотношением, называются
подобными.
,
связанные таким соотношением, называются
подобными.
Легко видеть, что детерминанты подобных матриц совпадают.
Введем теперь понятие ранга линейного оператора.
По определению это число, равное размерности образа данного оператора:
![]()
Докажем следующее важное утверждение:
Утверждение 1. 10 Ранг линейного оператора совпадает с рангом его матрицы, независимо от выбора базисов.
Доказательство. Прежде всего,
заметим, что образ линейного оператора
есть линейная оболочка системы
![]() ,
где
,
где
![]() -
базис в пространстве
-
базис в пространстве
![]() .
.
Действительно,
![]()
каковы бы ни были числа
![]() ,
но это и означает, что
,
но это и означает, что
![]() является указанной линейной оболочкой.
является указанной линейной оболочкой.
Размерность линейной оболочки, как мы знаем (см. п. 1.2) совпадает с рангом соответствующей системы векторов.
Мы ранее доказали (п. 1.3), что если система
векторов
![]() разложена
по некоторому базису
разложена
по некоторому базису
![]() в
виде
в
виде
![]() ,
,
то при условии независимости системы
![]() столбцы
матрицы
столбцы
матрицы
![]() линейно
независимы. Можно доказать и более
сильное утверждение (это доказательство
мы опускаем): ранг системы
линейно
независимы. Можно доказать и более
сильное утверждение (это доказательство
мы опускаем): ранг системы
![]() равен
рангу матрицы
равен
рангу матрицы
![]() ,
причем, этот результат не зависит от
выбора базиса, так как умножение матрицы
на невырожденную матрицу перехода не
меняет ее ранга.
,
причем, этот результат не зависит от
выбора базиса, так как умножение матрицы
на невырожденную матрицу перехода не
меняет ее ранга.
Поскольку
![]() ,
,
то
![]() .
.
Так как, очевидно, ранги подобных матриц совпадают, то данный результат не зависит от выбора конкретного базиса.
Утверждение доказано.
Для линейного преобразования некоторого конечномерного линейного пространства мы можем ввести и понятие детерминанта данного преобразования как детерминанта его матрицы в произвольно фиксированном базисе, ибо матрицы линейного преобразования в различных базисах подобны и имеют, следовательно, одинаковые детерминанты.
Используя понятие матрицы линейного
оператора, докажем следующее важное
соотношение: для любого линейного
преобразования
![]()
![]() -мерного
линейного пространства
-мерного
линейного пространства
![]()
![]()
Выберем произвольно базис
![]() в
пространстве
в
пространстве
![]() .
Тогда ядро
.
Тогда ядро
![]() состоит из тех и только тех векторов,
столбцы координат которых суть решения
однородной системы
состоит из тех и только тех векторов,
столбцы координат которых суть решения
однородной системы
![]() ,
(1)
,
(1)
а именно, вектор
![]() тогда и только тогда, когда столбец
тогда и только тогда, когда столбец
![]() есть
решение системы (1).
есть
решение системы (1).
Другими словами, имеет место изоморфизм
ядра
![]() на пространство решений системы (1).
Следовательно, размерности этих
пространств совпадают. Но размерность
пространства решений системы (1) равна,
как мы уже знаем,
на пространство решений системы (1).
Следовательно, размерности этих
пространств совпадают. Но размерность
пространства решений системы (1) равна,
как мы уже знаем,
![]() ,
где
,
где
![]() - ранг матрицы
- ранг матрицы
![]() .
Но мы только что доказали, что
.
Но мы только что доказали, что
![]() ,
,
откуда
![]() ,
,
что и требовалось.
Итак, любой линейный оператор, действующий из одного конечномерного линейного пространства в другое, однозначно может быть представлен в виде матрицы при фиксировании в каждом из пространств некоторого базиса.
Оказывается, что, в определенном смысле, верно и обратное.
Теорема 1.4 Какова бы ни была матрица
![]() и линейные пространства
и линейные пространства
![]() и
и
![]() ,
а также базисы
,
а также базисы
![]() и
и![]() в
в
![]() и
и
![]() соответственно, то однозначно определен
линейный оператор
соответственно, то однозначно определен
линейный оператор![]() из
из
![]() в
в
![]() такой, что его матрица в указанной паре
базисов совпадает с исходной матрицей
такой, что его матрица в указанной паре
базисов совпадает с исходной матрицей
![]() .
.
Доказательство. Отображение![]() из
из
![]() в
в
![]() определим так:
определим так:
![]() .
(2)
.
(2)
(т.е., если расписать подробно, через координаты, то
![]() ).
).
Линейность данного отображения легко проверяется.
То, что матрица
![]() в
данной паре базисов совпадает с
в
данной паре базисов совпадает с
![]() ,
следует непосредственно из выражения
(2).
,
следует непосредственно из выражения
(2).
Теорема доказана.
Таким образом, не только линейный оператор имеет матрицу в данной паре базисов, но и любая матрица определяет - при фиксированной паре базисов - линейный оператор. Это соответствие того же порядка, что и соответствие между любыми векторами, элементами конечномерных линейных пространств, и арифметическими векторами.
Последнее наблюдение может быть выражено и строго алгебраически, в терминах изоморфизма линейных пространств.
С этой целью необходимо установить соответствие между алгеброй линейных операторов и матричной алгеброй. Это соответствие оформим в виде следующей теоремы:
Теорема 1.5 Имеют место следующие
соотношения (для любых линейных операторов
![]() и
любого действительного числа
и
любого действительного числа
![]() ):
):
-

-

-
 (матрица нулевого оператора - нулевая)
(матрица нулевого оператора - нулевая) -
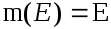 (матрица тождественного оператора -
единичная)
(матрица тождественного оператора -
единичная) -
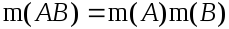
-

(Более подробно: линейный оператор обратим тогда и только тогда, когда, когда его матрица в любой паре базисов обратима, причем матрица обратного оператора есть обратная к матрице исходного оператора).
Доказательство сводится к простой проверке.
Следствие 1.3
![]() ,
где
,
где
![]() .
.
Итак, подобно тому, как любое конечномерное линейное пространство изоморфно арифметическому векторному пространству подходящей размерности, так пространство линейных операторов, действующих из одного конечномерного линейного пространства в другое, изоморфно пространству матриц подходящего размера (см. п. 1.1). В этом смысле линейные операторы и матрицы можно в конечномерном случае отождествить, как можно отождествить в том же случае произвольные векторы и арифметические векторы.
1.10. Ортогональное дополнение
Определение 1.16 Пусть
![]() - подпространство евклидова пространства
- подпространство евклидова пространства
![]() .
.
Ортогональным дополнением
подпространства
![]() называется такое множество векторов
называется такое множество векторов
![]() , что
, что
![]() .
.
Утверждение 1.11 Ортогональное
дополнение
![]() есть подпространство
есть подпространство
![]() (каково бы ни было подпространство
(каково бы ни было подпространство
![]() ).
).
Доказательство. Из свойств скалярного
умножения ясно, что для любых
![]()
![]() (каков бы ни был вектор
(каков бы ни был вектор
![]() ).
Тем самым вместе с любыми двумя векторами
ортогональное дополнение содержит их
сумму. Аналогично - для умножения на
число.
).
Тем самым вместе с любыми двумя векторами
ортогональное дополнение содержит их
сумму. Аналогично - для умножения на
число.
Утверждение 1.12 Для любых ненулевых
векторов
![]() и
и
![]()
![]() .
.
Доказательство очевидно.
Утверждение 1.13
![]()
Доказательство. Предположим, что
существует ненулевой вектор
![]() .
Тогда должно быть
.
Тогда должно быть
![]() ,
что невозможно.
,
что невозможно.
Утверждение 1.14
![]()
Утверждение 1.15
![]() .
.
Доказательство 1.14 и 1.15 очевидно.
Пусть теперь в подпространстве
![]() задан ортонормированный базис
задан ортонормированный базис
![]() .
Введем также ортонормированный базис
во всем пространстве
.
Введем также ортонормированный базис
во всем пространстве
![]() :
:
![]() ,
и пусть
,
и пусть
![]() - обычное разложение системы
- обычное разложение системы
![]() по
базису
по
базису
![]() .
Тогда, если вектор
.
Тогда, если вектор
![]() ,
то
,
то
![]() тогда
и только тогда, когда столбец
тогда
и только тогда, когда столбец
![]() есть
решение однородной системы
есть
решение однородной системы
![]() (1)
(1)
(действительно, каждый столбец матрицы
![]() есть столбец координат соответствующего
вектора базиса
есть столбец координат соответствующего
вектора базиса
![]() в
базисе
в
базисе
![]() ,
а при скалярном перемножении векторов
,
а при скалярном перемножении векторов
![]() ,
заданных разложениями в ортонормированном
базисе
,
заданных разложениями в ортонормированном
базисе
![]() .
.
Размерность пространства решений
системы (1) равна
![]() .
Значит,
.
Значит,
![]() (2)
(2)
Тем самым мы доказали, что имеет место
разложение произвольного конечномерного
евклидова пространства
![]() в виде объединения некоторого его
подпространства
в виде объединения некоторого его
подпространства
![]() и
его ортогонального дополнения:
и
его ортогонального дополнения:
![]() ,
причем
,
причем
подпространства
![]() и
и
![]() не имеют общих точек, кроме нулевого
вектора, и выполняется соотношение
размерностей (2).
не имеют общих точек, кроме нулевого
вектора, и выполняется соотношение
размерностей (2).
Такое разложение евклидова пространства называется разложением в прямую сумму двух подпространств, каждое из которых служит ортогональным дополнением другого. Это записывают в виде:
![]()
Например,
![]() ,
,
т.е., пространство геометрических
векторов раскладывается в прямую сумму
подпространства всех векторов,
параллельных плоскости
![]() ,
и всех векторов, параллельных оси
аппликат.
,
и всех векторов, параллельных оси
аппликат.
Более общо, если в пространстве фиксировать
некоторую плоскость
![]() ,
то пространство геометрических векторов
,
то пространство геометрических векторов
![]() раскладывается в прямую сумму:
раскладывается в прямую сумму:
![]() ,
,
где
![]() -
подпространство всех векторов,
параллельных плоскости
-
подпространство всех векторов,
параллельных плоскости
![]() ,
а
,
а
![]() - подпространство всех векторов,
параллельных прямой
- подпространство всех векторов,
параллельных прямой
![]() .
.
