2 курс Метрология (коллоквиумы, лабы) / задачи и д-з № 1 для П-202

10

1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СЛУЧАЙНЫЕ ПОГРЕШНОСТИ

Результат каждого отдельного измерения при наличии случайной погрешности невозможно заранее предсказать. Но повторные измерения обнаруживают закономерность. Математический аппарат для изучения таких закономерностей дает теория вероятностей. Отдельный возможный исход измерения - это случайное событие.

Количественная мера возможности реализации случайного события А называется его вероятностью:

(1.1)

где n(А) - число появлений события А ;

n - общее число испытаний (измерений).

Вероятность невозможного события равна нулю, а достоверного события Р(А)=1:

. (1.2)

Если события A₁, A₂, ... А_m несовместимы между собой и в сумме составляют достоверное событие, то события A₁, A₂, …, A_m образуют полную группу событий. Сумма вероятностей несовместимых событий, составляющих полную группу, равна единице, т.е.

. (1.3)

Среди случайных величин, с которыми приходится встречаться в технике измерений, можно выделить два основных типа : дискретные и непрерывные.

Дискретной случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений. Дискретное распределение считается заданным, если известны все возможные значения х₁, x₂, …, x_n, принимаемые величиной n вероятности P(x_i) для каждого события x=x_i. Эти события должны образовывать полную группу (1.3).

Функцию распределения дискретной величины считаем ступенчатой, принимая конечное или счетное число различных значений

(1.4)

Величина x называется непрерывной случайной величиной, если вероятность попадания ее значения в любой интервал (x₁, x₂) может быть представлена в виде интеграла

, (1.5)

где f(x) - плотность распределения вероятностей определяет закон распределения случайной величины; при этом функция f(x) неотрицательна и должна быть нормирована условием

,

отражающим достоверность события .

Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е.

. (1.6)

Характеристикой среднего значения случайной величины служит математическое ожидание, которое для дискретной случайной величины равно

, (1.7)

для непрерывной случайной величины

. (1.8)

Дисперсией случайной величины x называют математическое ожидание квадрата отклонения :

, (1.9)

дисперсию удобно вычислять по формуле

. (1.10)

Средним квадратическим отклонением случайной величины называют

квадратный корень из дисперсии

. (1.11)

Начальным моментом порядка k случайной величины x называют математическое ожидание величины x^k:

. (1.12)

В частности, начальный момент первого порядка равен математическому ожиданию:

.

Центральным моментом порядки k случайной величины X называют математическое ожидание величины :

. (1.13)

В частности, центральный момент первого порядка равен нулю :

;

центральный момент второго порядка равен дисперсии :

.

При непрерывном распределении весь интервал (x₁, x_n), в котором распределены все наблюдения, разбивают не ряд частичных интервалов длины h и находят n_i - сумму частот вариант, попевших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению n_i/h (плотность частоты). Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.

Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр. Доверительным называют интервал, который с заданной надежностью P покрывает оцениваемый параметр.

Доверительный интервал оценки математического ожидания нормально распределенной величины x по выборочной средней при известном генеральной совокупности равен

, (1.14)

где n - объем выборки;

Z есть такое значение аргумента функции Лапласа Ф(Z) (приложение 1), при котором .

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу Н_о.

Конкурирующей (альтернативной) называем гипотезу Н₁, которая противоречит нулевой.

В итоге проверки, гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают через . Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность ошибки второго рода - .

Статистическим критерием называют случайную величину K, которая служит для проверки гипотезы. Наблюдаемым значением K_набл называют то значение критерия, которое вычислено по выборкам.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Сравнение двух дисперсий нормальных генеральных совокупностей по независимым выборкам n₁ и n₂ и найденным выборочным дисперсиям S₁² и S₂² осуществляется по таблице критических точек распределения Фишера-Снедекора F_кр(; k₁, k₂) (приложение 2), по заданному уровню значимости и числам степеней свободы k₁=n₁-1 большей дисперсии, k₂=n₂-1.

Для того чтобы при заданном уровне значимости проверить нулевую гипотезу Н₀: D₁(x)=D₂(x) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: D₁(x)>D₂(x), надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии S_Б² к меньшей S_М²)

, (1.15)

если F_набл<F_кр - нет оснований отвергать нулевую гипотезу;

если F_набл>F_кр - нулевую гипотезу отвергают.

При проверке гипотезы о том, что генеральная совокупность x распределена нормально, чаще всего используют критерий Пирсона -

Для того чтобы при уровне значимости проверить гипотезу о нормальном распределении генеральной совокупности, надо:

1) эмпирическое распределение задать в виде последовательности интервалов (x_i, x_i+1) и, соответствующих им частот n_i:

(x₁, x₂) (x₂, x₃) ….. (x_m, x_m+1)

n₁ n₂ n_{m ;}

2) вычислить выборочную среднюю и выборочное среднее квадратическое отклонение , причем в качестве вариант x_i^* принимают среднее арифметическое концов интервала:

; (1.16)

3) пронормировать x, т.е. перейти к случайной величине и

вычислить концы интервалов :

, , (1.17)

причем наименьшее , а наибольшее ;

4) вычислить теоретические частоты

, (1.18)

где n - объем выборки;

- вероятность попаданий x в интервалы (x_i, x_i+1);

Ф(z) - Функция Лапласа;

5) сравнить эмпирические и теоретические частоты с помощью критерия Пирсона:

. (1.19)

По таблице критических точек распределения (приложение 3) по заданному уровню значимости и числу степеней свободы k=m-3 находят критическую точку правосторонней критической области .

Если - нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности ;

если - гипотезу отвергают.

Аудиторная работа

1.1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины x, заданной законом распределения:

а) x -4 6 10 б) х 0,2l 0,54 0,61

p 0,2 0,3 0,5 р 0,1 0,6 0,4

1.2. Случайные величины x и y независимы. Найти дисперсию случайной величины z = 2х + Зу, если известно, что D[x]= 4, D[y] = 5.

1.3. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины х, заданной законом распределения:

x -5 2 3 4 ;

р 0,4 0,3 0,1 0,2

1.4. Дискретная случайная величина х задана законом распределения :

х 1 3

р 0,4 0,6

Найти начальные моменты первого, второго и третьего порядков.

1.5. Дискретная случайная величина х задана законом распределения :

а) х 1 2 4 б) х 3 5

р 0,1 0,3 0,6; р 0,2 0,8.

Найти центральные моменты первого, второго, третьего и четвертого порядков.

2. ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ

2.1. Основные определения и формулы

Разность между результатом измерения Х_и и истинным значением измеряемой величины X называется абсолютной погрешностью результата измерения:

(2.1)

Погрешность является случайной величиной. Она может быть представлена в виде

, (2.2)

где - математическое ожидание величина , а - случайная величина с нулевым математическим ожиданием. Неслучайную величину называют систематической погрешностью, а - случайной погрешностью. Если значение известно, то систематическую погрешность можно исключить, приняв за окончательный результат измерения Х_испр, исправленный результат измерения:

(2.3)

Случайную погрешность исключить нельзя, так как неизвестно, какое конкретное значение приняла случайная величина при данном измерении. Для, оценки влияния случайной погрешности на результат измерения задают границы измерения случайной погрешности ₁ и ₂ и находят вероятность того, что измеряемая величина X заключена между (Х_и-₂) и (Х_и+₁). Интервал [Х_и-₂; Х_и+₁] называется доверительным интервалом, а вероятность того, что X находится внутри этого интервала - доверительной вероятностью Р_д. Можно показать, что

(2.4)

Если выбирают ₁= ₂, то .

Если известен дифференциальный закон распределения погрешности ,т.е. плотность вероятности f(), то

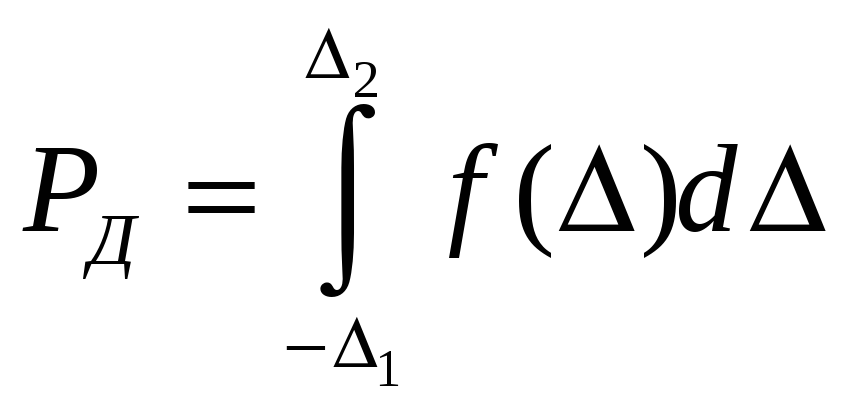(2.5)

Числовые характеристики закона распределения f(), математическое ожидание , дисперсия D и среднее квадратическое отклонение могут быть определены по формулам:

; (2.6)

; (2.7)

. (2.8)

При нормальном законе распределения погрешностей

. (2.9)

В этом случае, пользуясь таблицей функции Лапласа Ф(z) можно определить

. (2.10)

При использовании функции Лапласа необходимо учитывать, что

Ф(-z)=-Ф(z). (2.11)

В ряде случаев закон распределения погрешностей неизвестен, однако известны (обычно приближенно) его числовые характеристики и . Тогда для грубой оценки снизу доверительной вероятности Р при заданном симметричном доверительном интервале ₁ можно воспользоваться неравенством Чебышева

, (2.12)

откуда

. (2.13)

Если закон распределения погрешностей f(), а также его числовые характеристики и неизвестны, то можно найти их приближенно, располагая результатами ряда независимых измерений (наблюдений) одной и той же величины. Приближенные значения величин и называют оценками.

Если произведено n независимых наблюдений одного и того же известного значения X и получены результаты X₁, Х₂,...,Х­_n, то

; (2.14)

. (2.15)

При неизвестной величине X найти оценку систематической погрешности невозможно. Если в рассматриваемом случае можно пренебречь систематической погрешностью, то в качестве оценки истинного значения измеряемой величины следует принять среднее арифметическое результатов наблюдений:

. (2.16)

Среднее квадратическое отклонение величины X равно

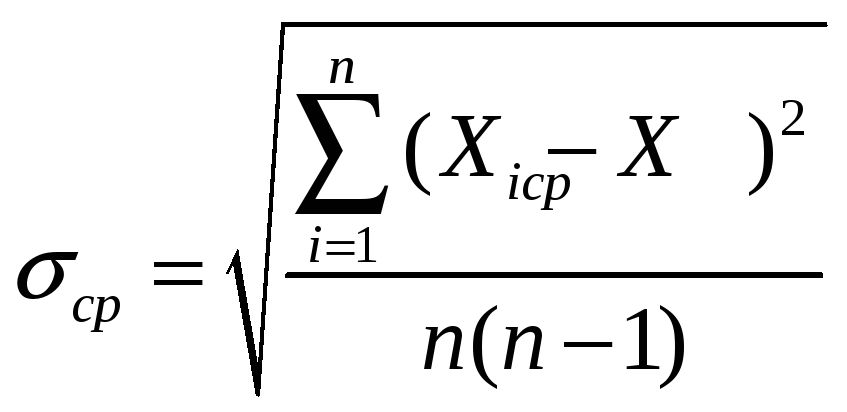. (2.17)

Среднее квадратическое отклонение каждого отдельного наблюдения, характеризующее точность метода измерения, при этом равно

. (2.18)

Предполагая, что закон распределения среднего арифметического результатов наблюдений близок к нормальному (имеет место при достаточно большом числе наблюдений), и пренебрегая систематической погрешностью, можно определить

. (2.19)

Если известно, что погрешности отдельных наблюдений распределены по нормальному закону (параметры которого неизвестны), то вместо приближенной формулы (2.19) следует использовать точное выражение

, (2.20)

где P_n(t) - интегральная функция распределения Стьюдента (приложение 4). Выражение (2.20) справедливо для любых n, больших единицы.

Если число наблюдения, n мало (n<10…20), а закон распределения погрешностей отдельных наблюдений нельзя считать близким к нормальному, то в этом случае для оценки величины Р_Д имеет смысл использовать выражение (2.13), положив = _ср.

Аудиторная работа

2.1. Погрешность измерения напряжения U распределена по нормальному закону, причем систематическая погрешность U₀ равна нулю, а = 50 мВ.

Найдите вероятность того, что результат измерения U_и отличается от истинного значения напряжения 0 не более чем на 120 мВ.

2.2. Решите задачу 1 при условии, что систематическая погрешность U₀ равна 30 мВ.

2.3. В результате проверки амперметра установлено, что 80% погрешностей результатов измерений, проведенных с его помощью, не превосходят 20 мА. Считая, что погрешности распределены по нормальному закону с нулевым математическим ожиданием, найдите вероятность того, что погрешность результата измерения превзойдет 40 mА.

2.4. В задаче 3 найдите симметричный; доверительный интервал для погрешности, вероятность попадания в который равна 0,5.

2.5. Результат измерения тока содержит случайную погрешность, распределенную по нормальному закону, равно 4 мА, _c равно нулю. Какова вероятность того, что погрешность превысит по абсолютной величине 12 мА?

2.6. В результате проверки амперметра установлено, что 70% погрешностей результатов измерений, произведенных с его помощью не превосходят 20 мА. Считая, что погрешности распределены по нормальному закону с нулевым математическим ожиданием, определите среднюю квадратическую погрешность,

Задание на дом

П-202

1. Может ли при каком-либо значении аргумента быть: 1) функция распределения больше единицы; 2) плотность распределения больше единицы; 3) функция распределении отрицательной; 4) плотность распределения отрицательной?

2. Дискретная случайная величина задана законом распределения:

х 3 4 7 10

р 0,2 0,1 0,4 0,3;

Найти интегральную функцию и построить ее график.

3. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение случайной величины x, заданной интегральной функцией:

4. Погрешность результата измерения тока распределена равномерно в интервале от -1 до +3 мА. Найдите: систематическую погрешность результата измерения; среднее квадратическое отклонение результата измерения; вероятность того, что исправленный результат измерения отличается от истинного значения измеряемого тока не более чем на 1 мА.