2.2 Особенности зарядового состояния наноразмерных частиц

К числу наиболее распространенных модификаторов нанокомпозиционных материалов, как ранее отмечалось, относятся металлические и металлсодержащие (оксиды, соли, нитриды, карбиды, бориды и др.) соединения, углеродсодержащие компоненты (УДАГ, УДА, фуллерены, углеродные нанотрубки, нановолокна и др.), природные силикатсодержащие соединения (слоистые минералы, цеолиты, граниты, туфы, серпентиты и т. п.).

Особое внимание уделяют геомодификаторам, которые обладают практически неограниченной сырьевой базой, а по эффективности действия, технологии получения и применения, стоимостным показателям существенно превосходят другие виды низкоразмерных частиц [25-27]. Применению слоистых минералов (глин) при создании наполненных композитов на основе термопластов обязано и появление самого термина нанокомпозиты [18].

2.2.1 Зарядовое состояние дисперсных частиц слоистых минералов

Типичным представителем слоистых минералов являются слюды, поэтому этот тип геомодикаторов удобно использовать для модельных исследований механизма образования у частиц нескомпенсированного заряда с большим временем релаксации [25].

Как отмечалось выше, слоистые силикаты – природные неорганические двухмерные полимеры [28] – характеризуются весьма совершенной спайностью, когда в элементарном структурном блоке межатомные связи ионно-ковалентные, а связи между блоками – Ван-дер-ваальсовые. В слюдах, как типичных представителях природных слоистых силикатов, в межблочных (межслоевых) промежутках располагаются ионы металлов (K, Na, Li, Ca и др), которые при расщеплении кристалла переходят на одну из ювенильных поверхностей и, вследствие различий в распределении дефектов в прилегающих к межслоевому промежутку элементарных слюдяных блоках, приводят к появлению на них электростатической мозаики [25]. Эта зарядовая мозаика, во-первых, сохраняется в течение достаточно длительного (до десятков минут) времени, а во-вторых, обусловливает модифицирующее действие частиц наномодификаторов в композиционных материалах с полимерной матрицей [19-21].

Электретные свойства различных диэлектриков исследуются уже в течение многих десятилетий, но интерес к зарядовому состоянию этих материалов не угас и в наше время. В частности, для примера, можно привести работы, опубликованные в последние годы [29-33]. Такие диэлектрики как слюды в наибольшей степени изучены в работах [34-35].

Слюда не только типичный слоистый геосиликат, но и как диэлектрик является достаточно типичным электретным материалом [35]. Следовательно, ее поверхностную активность можно повысить соответствующей обработкой электромагнитными полями. Задача облегчается тем, что в структуре слюд имеется диполь гидроксила, а в алюмо-кислородном тетраэдре одна из внутренних связей кислорода оказывается нескомпенсированной. При получении слюдяных чешуек с наноразмерной толщиной при разрушении макрокристалла могут проявиться термо-, механо- и трибоэлектретные свойства этих кристаллов [34]. В то же время установлено, что слюды являются устойчивыми и достаточно сильными короноэлектретами, в которых поверхностная плотность заряда может достигать  Кл/ [35]. Для измерения поверхностного заряда на слюдяной монокристальной пластинке используют как метод определения электростатической индукции, так и вибрационный метод. Схема последнего приведена на рис. 2.21 [36].

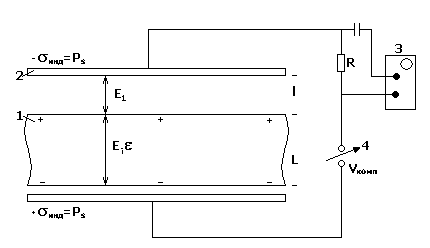
Рисунок 2.21 – Принципиальная схема вибрационного метода:1 – образец, 2 – вибрирующий электрод, 3 – индикатор нуля, 4 – измеритель компенсирующего потенциала, – поверхностная плотность зарядов

На вибрирующий электрод подается компенсирующий потенциал такой величины, что результирующий потенциал равен нулю. Естественно, поле электрета и поле пульсирующего потенциала противонаправлены. В этом случае компенсирующий потенциал равен потенциалу электрета плюс потенциал зазора кристалл-электрод . Потенциал заряда (см. рис. 2.21), определяется отношением:

(2.91)

где – диэлектрическая проницаемость электрета. Так как , то .

Электрод колеблется с частотой и с амплитудой , то есть

. (2.92)

В цепи возникает переменный ток, компенсируемый источником ЭДС (рис. 2.21).

В общем случае поверхностный заряд электрета обусловлен алгебраической суммой зарядов в поверхностном слое (так называемый, гомозаряд) и заряда, наведенного за счет остаточной объемной поляризации диэлектрика (гетерозаряда). Гомозаряд располагается в тонком поверхностном слое электрета (у электродов). Гетерозаряд можно объяснить накоплением в объеме электрета освобожденных из центров захвата слабосвязанных зарядов, участвующих в электропроводности. В соответствии с законом Больцмана всегда имеется равновесная концентрация свободных заряженных частиц :

, (2.93)

где – энергия активации заряженных частиц (ионов или электронов), – постоянная Больцмана, – температура, – число неактивированных частиц ( ).

Освобождающиеся заряженные частицы движутся в электрическом поле к электродам. При этом они захватываются более глубокими энергетическими ловушками на структурных дефектах электрета и образуют, прочно связанные с электретом объемные заряды, что обусловливает внутреннюю поляризацию. Заряды как бы «перегоняются» из мелких «ловушек» в более глубокие [35, 36].

При отсутствии дополнительных более глубоких ловушек эти заряды рассеиваются. Электрет, теряя свою поляризацию, разряжается. Энергию активации зарядов , а также их концентрацию , можно определить, нагревая электрет. При его термической активации методом термостимулированной деполяризации (ТСД) электрет помещают в печь с линейным нагревом

, (2.94)

где – время, – скорость нагревания.

Ток, протекающий через электрет, с уменьшением температуры растет, проходит через максимум (рис. 2.22) и затем убывает до нуля. Зависимость может иметь несколько максимумов. Например, как показано в работе [35], у мусковита эти максимумы встречаются в интервале температур и при .

Площадь под кривой ТСД определяет накопленный в электрете заряд, так как

. (2.95)

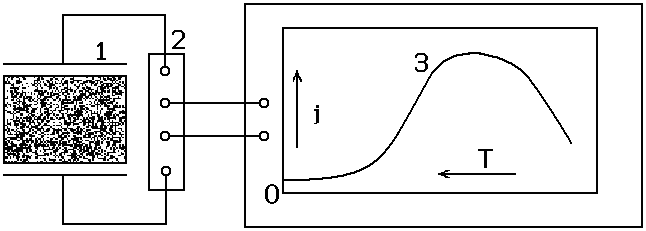
Рисунок 2.22 – Принципиальная схема измерения токов ТСД: 1 – нагреватель электрета, 2 – самописец, 3 – кривая ТСД ( )

Если – вектор поляризации, равный плотности связанных зарядов, то вектор плотности тока деполяризации определяется уравнением:

. (2.96)

В уравнении (2.97) показатель – частотный фактор, определяемый условием:

(2.97)

где – энергия закрепления зарядов (электронов, ионов) в ловушках электрета, – частота их колебаний при температуре , – частота их колебаний при температуре .

Из условий (2.95, 2.97) получим

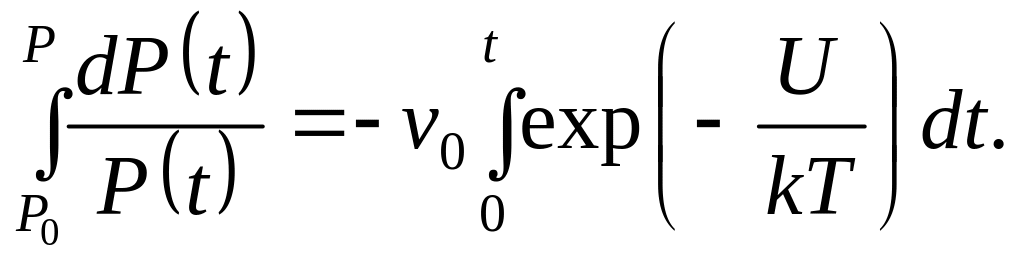(2.98)

или

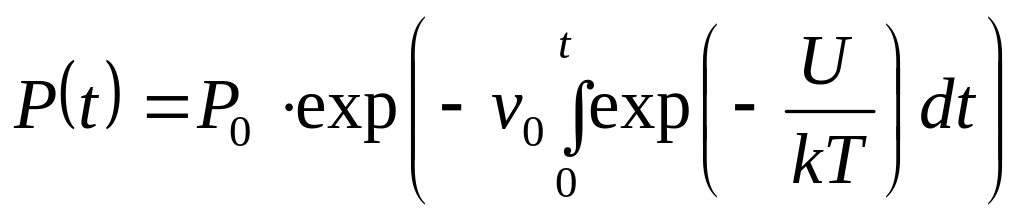. (2.99)

Если скорость нагревания постоянна ( ), то функция трансформируется в функцию . С учетом (2.95, 2.97, 2.99) получим:

(2.100)

Зависимость энергии от температуры в общем случае функция неизвестная, поэтому, несмотря на простоту записи этого интеграла, в общем виде он не определим. Следовательно, зависимость тока деполяризации от температуры, во-первых, носит сложный характер, во-вторых, различна как для различных электретов, так и для и скорости изменения температуры. В самом общем случае, когда , величину так же следует вводить под знак интеграла.

Из условия (2.100) для интервала температур следует:

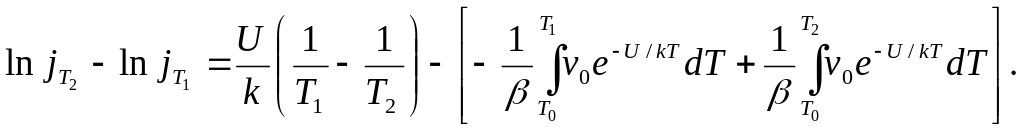(2.101)

Если интервал не очень велик , то области интегрирования для слагаемых в квадратных скобках отличаются друг от друга относительно слабо, тогда из (2.101) следует, что в интервале температур энергия локализации зарядов имеет вид:

(2.102)

Следовательно, по зависимостям (см. рис. 2.22) при изучении токов термостимулированной деполяризации можно определить энергию локализации носителей зарядов в электретах [35, 36].

Как показали исследования, описанные в работе [35], поляризацию кристаллов слюды в поле коронного разряда следует осуществлять при потенциалах до 50 кВ. Экспериментальные зависимости электретного потенциала от времени действия коронного разряда для его различных потенциалов и при различных толщинах слюдяных пленок представлены на рис. 2.23. Зависимость описывается уравнением

(2.103)

где – максимально достижимый электретный потенциал, – постоянная времени поляризации электрета.

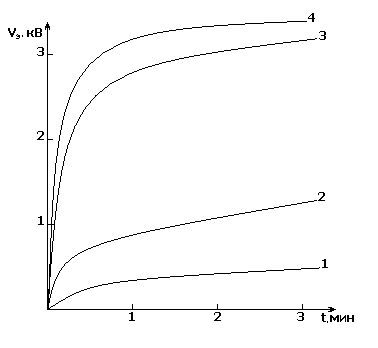
Рисунок 2.23 – Кинетика поляризации кристаллов мусковита при потенциалах короны: 1, 2 – 10 кВ; 3, 4 – 40 кВ для толщин кристаллов 9 и 12 мкм соответственно [35]

Величина максимального электретного потенциала увеличивается пропорционально толщине слюдяной пластины до значений примерно 12 мкм и ограничивается их диэлектрической прочностью. При потенциале электрического поля =3,6 кВ в слюдяной пластине толщиной 12 мкм и значение равно примерно В/см, то есть имеет порядок электрической прочности мусковита в неоднородном электрическом поле [35]. По-видимому, при в кристалле происходят микропробои, ограничивающие дальнейший рост . Этим максимальным полям соответствует плотность поверхностного заряда, равная: , что примерно на два порядка больше, чем у многих электретов.

С ростом толщины кристаллов плотность поверхностного заряда существенно не увеличивается, вследствие рассеяния приповерхностных зарядов электрета тремя способами: газовыми ионами короны, объемной и поверхностной проводимостями образца и его локальными точечными электрическими пробоями. В процессе хранения электретов происходит их постепенная разрядка, в том числе и за счет адсорбционных процессов [36], особенно в первые минуты после снятия воздействия коронного разряда. Продолжительность дальнейшего спада определяется релаксацией приповерхностных объемных зарядов, созданных короной, механизмом дрейфа зарядов в собственном поле электрета. В этом случае постоянная релаксации имеет вид:

. (2.104)

Как показывают расчеты для мусковита сут., для флогопита сут. Эти результаты близки к измеряемым в эксперименте, когда величина электропроводности задается энергией активации зарядов , связанных с вакансиями ионов на поверхности кристалла. Дальнейшая разрядка электрета до значений В также обусловлена электропроводностью образца. Но эта электропроводность связана с освобождением зарядов из более глубоких центров локализации зарядов в кристаллах, в вакансиях с энергией  эВ. Расчет времени релаксации процессов такого типа приводят к значениям с >100 лет.

При рассмотрении электретных явлений в слюдах следует учитывать, что эти минералы весьма склонны к изоморфизму и в своем составе кроме гидроксильных групп в октаэдрической сетке имеют нейтральные молекулы воды (иногда оксония – ) в межслоевом промежутке (это наиболее свойственно триоктаэдрическим слюдам, например, флогопиту [28]), а также водные включения в виде тонких водных пленок и водных микролинз. Вследствие контактной разности потенциалов между различными веществами, например, водой в поре и твердой стенкой, они приобретают электрические заряды разных знаков (вода обычно заряжается положительно, твердое тело – отрицательно) [36]. На границе неоднородности появляется двойной электрический слой (рис. 2.24).

При внесении таких неоднородных материалов в электрическое поле свободные электроны и ионы, содержащиеся в проводящих включениях, начинают перемещаться в пределах каждого включения (неоднородности). Включение приобретает дипольный момент и ведет себя подобно гигантской поляризованной молекуле (рис. 2.24, в).

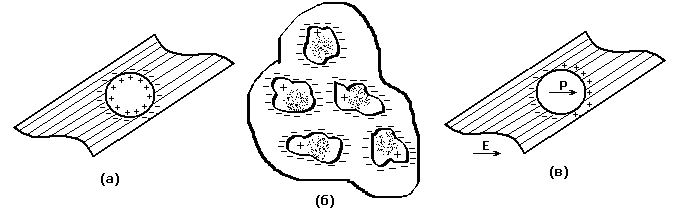
Рисунок 2.24 – Схема формирования двойного электрического слоя вокруг неоднородности в диэлектрике. (а) – с включениями воды; (б) – диэлектрик с порами заполненными водой; (в) – поляризация включения в электрическом поле

Таким образом, неоднородности в строении материала приводят к перемещению свободных зарядов в ограниченном объеме неоднородности, и в этом смысле, они оказываются подобными связанным зарядам. При изменении поля, дипольный момент единицы объема вещества , характеризующий такую структурную поляризацию, изменяется по условию, аналогичному (2.104):

(2.105)

где – постоянная времени структурной поляризации, которая может варьироваться для различных диэлектриков в широких пределах от 1 до с, – максимальная поляризация. – это время, за которое поляризация достигает 0,632 ее максимального значения. Действительно, в этом случае (см. 2.105) .

Макроструктурная поляризация может проявляться в очень широком диапазоне частот: от инфразвуковых до сверхвысоких. Величина времени релаксации поляризации водных включений в диэлектрике может быть определена из дисперсной кривой изменения емкости (поляризации Р) диэлектрика в зависимости от частоты, действующего на кристалл диэлектрического поля. Если – среднее время движения заряда между границами водного включения, то размер включения равен [36]:

(2.106)

где – подвижность ионов , – напряженность поля во включении, – размер включения. Эта формула носит приближенный характер, так как из нее следует, что при , хотя очевидно, что в этих условиях необходимо анализировать свойства объемного, то есть с бесконечно большим в физическом смысле, размером, вещества включения в диэлектрик.

Дисперсные частицы слоистых минералов, подвергнутые различным видам активационной обработки, использованы при создании функциональных нанокомпозитов [37], структура и характеристики которых будут рассмотрены далее.