
- •Содержание
- •Введение
- •Глава 1 особенности структуры и технологии наноразмерных объектов
- •1.1 Классификация вещественных объектов
- •1.1.1 Размерные классы частиц
- •1.1.2 Факторы, влияющие на свойства вещества
- •Риcунок 1.11 – Схема возникновения н-центра окраски в цгк типа NaCl
- •1.2 Методы получения низкоразмерных частиц
- •1.3 Модельные представления о структуре и габитусе наноразмерных частиц
- •1.3.1 Методологические подходы к описанию кристаллов
- •1.3.2 Правильные формы кристаллов и их описание
- •Общие простые формы кристаллов и кристаллографические индексы их граней (hkl)
- •Частные простые формы (грань (h 0 0))
- •Частные простые формы кристаллов с единичным направлением (исходная грань (h k 0)).
- •Частные простые формы кристаллов без единичного направления
- •1.3.3 Габитус наночастиц, полученных при диспергировании крупных кристаллов
- •1.4 Теоретическое описание структуры и габитуса наночастиц, полученных конденсированием
- •1.4.1 Шаровые упаковки как модели многоатомных структур
- •1.4.2 Атомные координации в полиэдрах плотнейших атомных упаковок
- •Радиусы координационных сфер и их числа заполнения для гцк-структур
- •Радиусы координационных сфер и их числа заполнения для гпу-структур
- •Радиусы координационных сфер и их числа заполнения для оцк-структур
- •1.4.3 Некристаллографическая симметрия габитуса наноразмерных атомных координационных полиэдров
- •1.4.4 Фуллереноподобные формы нанокристаллов
- •1.4.5 Габитусы наночастиц сложного состава
- •1.5 Структура и свойства наноразмерных частиц, применяемых в функциональном материаловедении
- •1.5.1 Структура и свойства наноразмерных металлических модификаторов функциональных материалов
- •Координационные числа (к) координационных сфер (n – ее номер) при плотнейшей шаровой упаковке
- •Основные параметры, необходимые для описания жидких кластеров металлов (z – порядковый номер, n – плотность атомов, ef – энергия Ферми, rw – радиус Вагнера-Зейтца, w – работа выхода)
- •1.5.2 Наноразмерные углеродсодержащие модификаторы*
- •Размеры кристаллических блоков в алмазосодержащих продуктах детонационного синтеза
- •Р исунок 1.66 – Термограммы tg (а) и dta (б) углеродных нанокластеров. Скорость нагрева 5оС/мин: 1 – удаг; 2 – уда
- •Фазовый состав наномодификаторов, полученных по технологии термолиза прекурсора в технологической среде
- •Характеристики модифицированных углеродных волокон [161]
- •1.5.3 Силикатные наноразмерные частицы
- •Кристаллографические индексы рефлексов (kl) и структурные амплитуды f(20) и f(850) кристалла мусковита при 20оС и после прогрева при 850оС соответственно
- •Характеристики ультрадисперсных керамик (ук), полученных плазмохимическим синтезом [179]
- •Характеристики ультрадисперсных керамик (ук) механохимического синтеза [177]
- •Характеристики ультрадисперсных оксинитридов плазмохимического синтеза [179-180]
- •Некоторые свойства природных и синтетических цеолитов
- •1.6 Заключение к главе 1
- •Глава 2 механизмы модифицирующего действия наноразмерных частиц в полимерных и олигомерных матрицах
- •2.1 Критерии оценки наноразмерности
- •2.1.1 Физические предпосылки к оценке наноразмерности частиц
- •2.1.2 Связь фононных характеристик с наноразмерностью
- •2.1.3 Теорема Блоха и наноразмерность
- •2.1.4 Дебаевская длина волны и максимальный наноразмер
- •2.1.5 Расчет максимального наноразмера на основании уравнения Шредингера
- •2.1.6 Определение предельных размеров частиц веществ с неразрушенными полимерными молекулами
- •2.1.7 Динамические модели кристалла Эйнштейна и Дебая
- •2.1.8 Расчетные значения максимальных размеров наночастиц одноэлементных веществ и некоторых соединений
- •Характеристические температуры ( ) и максимальные размерынанокристаллов некоторых веществ
- •Характеристические температуры и максимальные размеры нанокристаллов некоторых галогенидов
- •Температура Дебая и максимальный наноразмер полупроводников типов
- •Отношение температуры Дебая наночастиц к для объемной фазы некоторых металлов, r – размер частицы
- •Дебаевская температура и наноразмерный максимум одноэлементных веществ
- •2.1.9 Влияние размеров кристаллитов на их физические свойства
- •2.2 Особенности зарядового состояния наноразмерных частиц
- •2.2.1 Зарядовое состояние дисперсных частиц слоистых минералов
- •2.3 Зарядовое состояние металлических компонентов функциональных материалов и металлополимерных систем
- •2.3.1 Модельные представления о механизме модифицирования полимерных матриц нанокомпозиционными частицами
- •Зависимость размеров областей когерентного рассеяния (l ǻ) от массовой концентрации (с, мас.%) ультрадисперсного углерода (шихты)
- •Значения радиусов (r, ǻ) и относительных координационных чисел (окч) для композитов с различной массовой концентрацией (с, мас.%) наполнителя
- •2.4 Заключение к главе 2
2.1.7 Динамические модели кристалла Эйнштейна и Дебая
Атомы в конденсированных средах колеблются вокруг своих идеальных, то есть равновесных, положений. Следовательно, кристалл можно представить в виде системы взаимодействующих друг с другом осцилляторов. Двухмерная модель такого кристалла с точечной группой 4mm приведена на рис. 2.6. Очевидно, что все атомы в такой одноэлементной структуре находятся в одинаковых кристаллофизических позициях и, следовательно, изучив состояние любого из них, можно говорить о состоянии всей системы. В этой модели атомы как бы «связаны» друг с другом квазиупругой силой, а смещения от положения равновесий не очень велики, то есть можно считать, что все атомы совершают колебания с одинаковой частотой ω. Именно на этом предположении основана теория Эйнштейна, которая позволила объяснить отклонения значений теплоемкости веществ при низких температурах от закона Дюлонга и Пти [3, 7, 8].
Эйнштейн считал, что каждый из N атомов имеет 3 степени свободы, то есть в кристалле имеется 3N независимых гармонических осцилляторов, колеблющихся с одинаковой частотой ω, то есть обладающие энергией E=ħω (ħ – постоянная Планка).
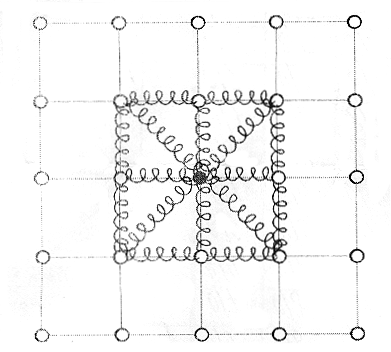
Рисунок 2.6 – Двухмерная модель структуры с точечной группой 4mm с упругим взаимодействием атомов
Принципы квантования допускают наличие состояний с энергией
![]() , (2.79)
, (2.79)
где n – целое число, нулевые колебания учитываются слагаемым 0,5ħω.
Распределение электронов по уровням энергий подчиняется закону Бозе-Эйнштейна, который с учетом нулевых колебаний при температуре Т имеет вид [6, 8]:
 . (2.80)
. (2.80)
Легче всего суммирование по всем значениям j выполняется для двух граничных случаев: высокая и низкая температуры [7, 8].
Если температура настолько высокая,
что
![]() ,
то при разложении в ряд экспоненты
знаменателя можно ограничиться вторым
членом разложения. В этом случае условие
(2.80) примет вид:
,
то при разложении в ряд экспоненты
знаменателя можно ограничиться вторым
членом разложения. В этом случае условие
(2.80) примет вид:
![]() .
(2.81)
.
(2.81)
Так как энергия нулевых колебаний много
меньше энергии решетки, то каждый из 3N
осцилляторов вносит вклад в общую
энергию, равный kT. Средняя энергия
гармонического осциллятора в модели
Эйнштейна при высоких температурах
совпадает с классической средней
энергией kT. То есть при
![]() для одного моля
для одного моля
![]() ,
где А
– постоянная Авогадро, R
– газовая постоянная, то есть выполняется
закон Дюлонга и
Пти
,
где А
– постоянная Авогадро, R
– газовая постоянная, то есть выполняется
закон Дюлонга и
Пти
![]() .
.
Колебания атомов в кристаллах, как и в любой конденсированной среде, приводят к тому, что в них создаются волны механического возбуждения, которые, как это следует из уравнения (2.79), описываются квантами механического возбуждения, называемых фононами [9].
При низких температурах собственная
частота фононов может быть такой, что
выполняется неравенство
![]() .
В этом случае
.
В этом случае
![]() .
В то же время, вклад этих составляющих
в общую энергию системы будет
незначительным, так как в спектре частот
их встречаемость невелика [5]. Следовательно,
можно ограничиться акустическими
ветвями фононов. Средняя энергия в этом
случае равна
.
В то же время, вклад этих составляющих
в общую энергию системы будет
незначительным, так как в спектре частот
их встречаемость невелика [5]. Следовательно,
можно ограничиться акустическими
ветвями фононов. Средняя энергия в этом
случае равна
![]() , (2.82)
, (2.82)
то есть теплоемкость при низких температурах (Т→0) определяется условием:
![]() . (2.83)
. (2.83)
Отсюда следует, что CV→0
при Т→0 по закону
![]() .
.
Теория Эйнштейна дает неплохое согласие с экспериментом (рис. 2.7).
Так как в модели Эйнштейна все осцилляторы
имеют одинаковую частоту (ω), то есть
одинаковую энергию, то для их описания
был введен температурный фактор
![]() вида
вида
![]() , (2.84)
, (2.84)
где – температура Эйнштейна.
В этом случае выражение для определения теплоемкости CV (2.84) с учетом (2.84) при Т→0 примет вид:
![]() . (2.85)
. (2.85)
Эта формула Эйнштейна, хотя и выведена
для условия Т→0, находится в хорошем
согласии с экспериментом и в области
температур, не сильно отличающихся от
.
Но эксперименты показывают, что при
температуре
![]() ,
CV зависит от Т не по
экспоненте, а скорее по зависимости
CV~Т3 [3].
,
CV зависит от Т не по
экспоненте, а скорее по зависимости
CV~Т3 [3].
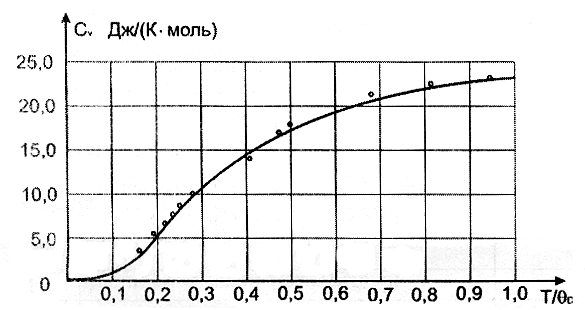
Рисунок 2.7 – Сопоставление экспериментальных данных для температурной зависимости теплоемкости алмаза с теоретической кривой, построенной на основе модели Эйнштейна, используя θЕ=1320°К
Для более строгой оценки зависимости CV от Т при низких температурах П. Дебай отказался от модели одинаковых атомных осцилляторов, а предположил, что в твердом теле атомы колеблются с различными частотами. Распределение частот осцилляторов описывается зависимостью P(ω), которая определяется условиями [14]:
![]() ,
(2.86)
,
(2.86)
где V – скорость распространения фононов.
В соответствии с предположением Дебая
частота ω может достичь некоторого
максимального значения
![]() ,
которое и называется дебаевской частотой,
а распределение P(ω) в модели Дебая
обладает свойствами [7]:
,
которое и называется дебаевской частотой,
а распределение P(ω) в модели Дебая
обладает свойствами [7]:
![]() .
(2.87)
.
(2.87)
Распределение фононных частот в моделях
Эйнштейна и Дебая иллюстрируются рис.
2.8. Это не означает, что частоты с
![]() в реальных кристаллах не существуют,
они есть, но для их описания нужны другие
теоретические модели [7, 8].
в реальных кристаллах не существуют,
они есть, но для их описания нужны другие
теоретические модели [7, 8].
При функции распределения частот (9) плотность внутренней энергии равна
![]() , (2.88)
, (2.88)
где U0 – энергия равновесного состояния решетки.
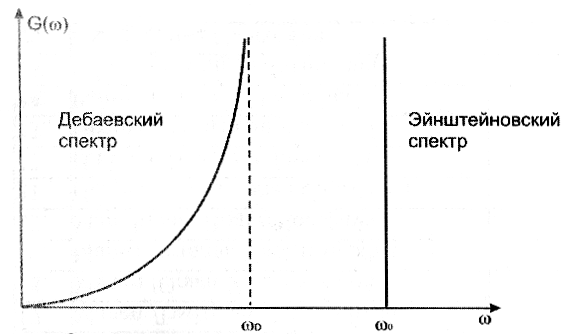
Рисунок 2.8 – Спектральная функция G(ω) в эйнштейновском и дебаевском приближениях
Переменная интегрирования x в выражении (2.88) меняется в пределах от 0 до Xm, равного
![]() , (2.89)
, (2.89)
где n – число атомов в единице объема
(атомная плотность), qm –
волновое число, V – скорость звука
[3, 10, 11]. Величина
![]() связана с дебаевской частотой уравнением
связана с дебаевской частотой уравнением
![]() . (2.90)
. (2.90)
Параметр
![]() называют дебаевской частотой.
называют дебаевской частотой.
При очень низких температурах
![]() верхний предел интеграла в выражении
(2.88) можно заменить на ∞ и тогда, как
показано в [8] (U-U0)~Т4,
то есть CV~Т3,
так как
верхний предел интеграла в выражении
(2.88) можно заменить на ∞ и тогда, как
показано в [8] (U-U0)~Т4,
то есть CV~Т3,
так как
![]() .
.
Если приближение Эйнштейна говорит об
экспоненциальной зависимости CV
от Т, то в дебаевской модели – CV~Т3,
что больше соответствует эксперименту.
Совпадение дебаевской теории с
экспериментальными данным иллюстрируется
рис. 2.9, на котором приведены значения
![]() для различных веществ. Следовательно,
верна гипотеза Дебая о том, что при
переходе под действием тех или иных
факторов значений частотных мод фононов
в область
,
механизм протекания физических процессов
изменится по сравнению с тем случаем,
когда в спектре имеются только частоты
для различных веществ. Следовательно,
верна гипотеза Дебая о том, что при
переходе под действием тех или иных
факторов значений частотных мод фононов
в область
,
механизм протекания физических процессов
изменится по сравнению с тем случаем,
когда в спектре имеются только частоты
![]() [2,12].
[2,12].
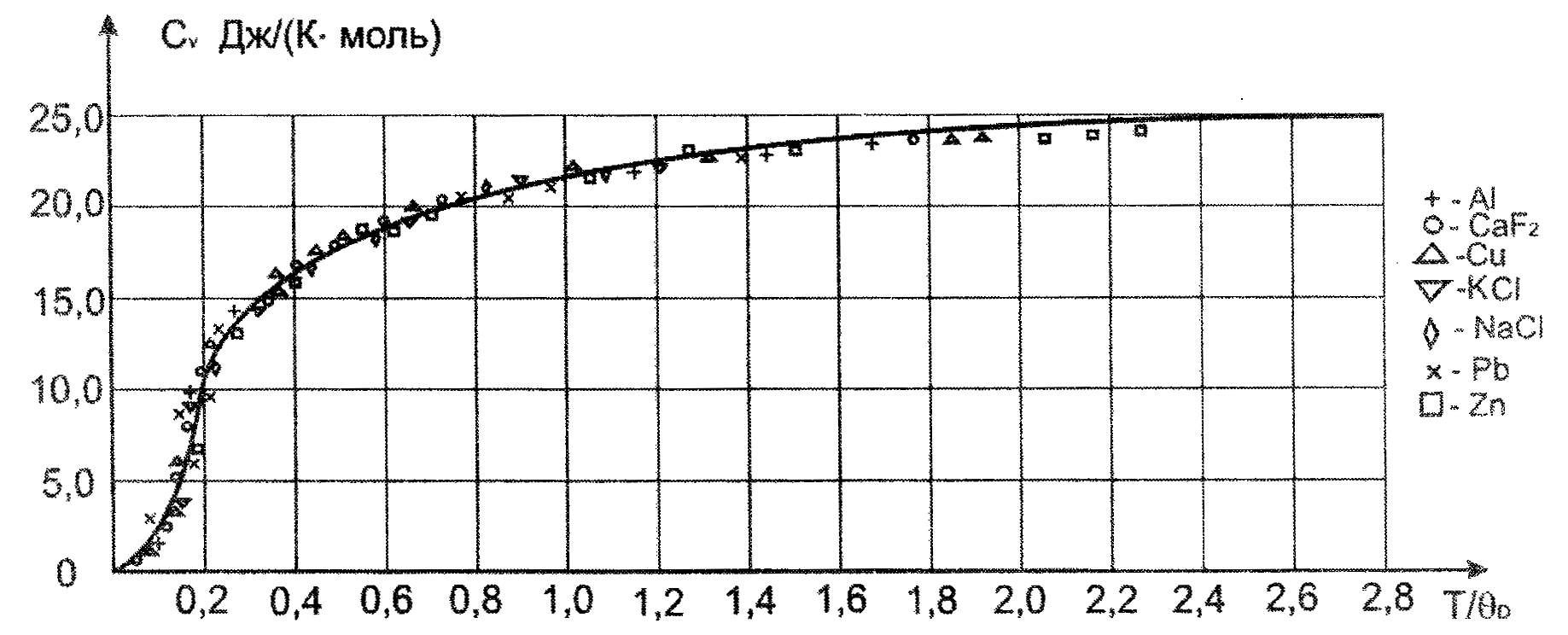
Рисунок 2.9 – Теплоемкость CV различных веществ в зависимости от отклонения температуры вещества к его дебаевской температуре. CV— теплоемкость при Т>θD.
Распределение частот в модели Дебая (рис. 2.10) является неплохим приближением для объяснения в области низких температур. Но в реальных кристаллах Р(ω) отличается от модели Дебая. Например, на рис. 2.10 приведено экспериментально полученное распределение Р(ω) для Al [5, 9] Распределение Р(ω) различно для различных веществ, но в любом случае функция Р(ω) имеет четко выраженный максимум .

Рисунок 2.10 – Спектр частот гармонических осцилляторов в Al
Модель Дебая, как и модель Эйнштейна, объясняет экспериментально обнаруженный факт уменьшения теплоемкости при постоянном объеме (CV) при температурах, ниже характеристической. Так как совпадения теории с экспериментом в модели Дебая существенно выше, чем в модели Эйнштейна, то первую модель используют чаще для анализа физических свойств веществ, но и модель Эйнштейна в ряде случаев дает удовлетворительные результаты [5, 9].
Распределение частот применимо для
описания образцов с достаточно большими
объемами веществ. В этом случае размер
образца не оказывает влияния на кривую
Р(ω). Из приведенного на рис. 2.10
примера видно, что в веществе имеется
две области частот: низкочастотная
ветвь
![]() и высокочастотная ветвь
.
Если размер кристалла достаточно мал,
то образование фононов с большими
длинами волн невозможно, то есть размер
кристалла «отсекает» в спектре
акустическую (низкочастотную) ветвь.
Когда минимальная частота фононов
превышает
,
то процессы, происходящие в образце,
отличаются от аналогичных в образцах
с большими геометрическими размерами.
Следовательно, если размер образца L
такой, что в нем не могут возникать
низкочастотные моды, у которых длина
волны больше, чем L, то физические
процессы в этом образце будут протекать
иначе, чем в крупном образце того же
вещества при той же температуре. Так
как в этом случае L0
соответствует условию
и высокочастотная ветвь
.
Если размер кристалла достаточно мал,
то образование фононов с большими
длинами волн невозможно, то есть размер
кристалла «отсекает» в спектре
акустическую (низкочастотную) ветвь.
Когда минимальная частота фононов
превышает
,
то процессы, происходящие в образце,
отличаются от аналогичных в образцах
с большими геометрическими размерами.
Следовательно, если размер образца L
такой, что в нем не могут возникать
низкочастотные моды, у которых длина
волны больше, чем L, то физические
процессы в этом образце будут протекать
иначе, чем в крупном образце того же
вещества при той же температуре. Так
как в этом случае L0
соответствует условию
![]() (u – скорость фонона), то можно сделать
следующий вывод. Для каждого вещества
существует граничный размер L0,
связанный с температурой Дебая
.
Если размер образца r>L0,
то этот образец обладает свойствами
крупных образцов, если r<L0,
то на свойства образца влияют размерные
факторы, то есть при дальнейшем уменьшении
размера частиц в них невозможно
существование возбуждений с дебаевской
частотой, так как дебаевская длина волны
не «вместится» между поверхностями
образца. L0 имеет размерность
в нанометровом диапазоне от 8 нм для
алмаза, до 30 нм для рубидия. У полимерных
объектов L0 может достигать
40 нм, но ни для одного вещества L0
даже не приближается к значению 100 нм
[14, 16, 23].
(u – скорость фонона), то можно сделать
следующий вывод. Для каждого вещества
существует граничный размер L0,
связанный с температурой Дебая
.
Если размер образца r>L0,
то этот образец обладает свойствами
крупных образцов, если r<L0,
то на свойства образца влияют размерные
факторы, то есть при дальнейшем уменьшении
размера частиц в них невозможно
существование возбуждений с дебаевской
частотой, так как дебаевская длина волны
не «вместится» между поверхностями
образца. L0 имеет размерность
в нанометровом диапазоне от 8 нм для
алмаза, до 30 нм для рубидия. У полимерных
объектов L0 может достигать
40 нм, но ни для одного вещества L0
даже не приближается к значению 100 нм
[14, 16, 23].
Влияние размерного фактора на характер протекания физических процессов рассмотрено в работе [24], в которой подчеркивается, что в наночастицах наблюдается «сочетание сильной пространственной локализации электронных колебаний с высокой частотой этих колебаний». Это приводит «к гигантскому увеличению... электрических полей». Оптические свойства наночастиц резко отличаются от аналогичных свойств объемного вещества.
