1.4.3 Некристаллографическая симметрия габитуса наноразмерных атомных координационных полиэдров
Если атомный полиэдр, сформированный вокруг отдельного атома, как это следует из таблиц, может иметь различное число атомов на координационных сферах, то есть характеризуется пониженной ретикулярной плотностью, то на его поверхность могут осаждаться атомы другой (последующей) координационной сферы с образованием даже более устойчивой структуры, по сравнению с полиэдром, ограниченным атомами одной координационной сферы. На эту особенность шаровых упаковок обратил внимание Н.В. Белов [54]. Примеры структуры полиэдра с некристаллографической симметрией приведены на рис. 1.41 и 1.42, которые взяты из работы [50]. В системе на рис. 1.41 – 42 «шара», что соответствует числу шаров в ГКЦ-упаковке. Но шары (здесь суббелковые частицы) внешнего слоя находятся на разных расстояниях. Эта частица сформирована по принципу «жадного алгоритма» (ЖА), когда ее формирование идет не вокруг центрального атома, а вокруг тетраэдра из четырех атомов (шаров). Атомы последующего слоя располагаются во впадине между тремя атомами предыдущего слоя, то есть опять формируется тетраэдр. Эта последовательность может быть выполнена в пределах ограниченного объема, в котором коэффициент компактности больше, чем в плотнейших ГЦК- и ГПУ-решетках. Именно поэтому такая упаковка получила название «жадного алгоритма». Такая частица очень устойчивая, трудно поддается влиянию внешних воздействий. Этот габитус свойственен многим вирусам, а возможно и другим частицам, которые влияют на нашу жизнь, а человек, к сожалению, часто бессилен перед миром нано- и микрочастиц (10–8 классы по классификации работы [45]).
При дальнейшем росте частицы, сформированной по жадному алгоритму соблюдения условия формирования по созданию тетраэдров приводит к резкому уменьшению коэффициента компактности, который уже в миллиметровом диапазоне размеров будет меньше, чем 0,740.
Если в полиэдре рисунка 1.42 продолжить пары граней вдоль осей x, y, z прямоугольных координатных систем отдельных частей приведенного многогранника, то будет получен куб, описанный вокруг триаконтаэдра.
Следует отметить, что рассмотренный метод анализа комплексов применим не только для моноатомных, но и для более сложных веществ. Крупные додекаэдрические молекулы, которые, вообще-то, проявляются в правильных формах кубических кристаллов [49], экспериментально обнаружены в структуре гидрата хлора Cl2∙8H2O (6Cl2∙48H2O).
Рисунок 1.41 – Раковый вирус с поверхностью идеального икосаэдра, образованной 42 сферическими суббелковыми частицами
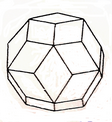
Рисунок 1.42 – Ромбический триаконтаэдр – простая форма некристаллографического класса 532/m (шесть осей L5, десять L3 и пятнадцать L2)
Каждая такая частица состоит из 20 молекулярных групп H2O, располагающихся по вершинам правильного или почти правильного додекаэдра, окружающего центральную H2O, вместо которой может быть взята и другая молекула (H2S, CH4). Такими молекулами-додекаэдрами, однако, невозможно выполнить пространство без пропуска, и в той же структуре гидрата хлора, помимо приходящихся на элементарную кубическую ячейку двух додекаэдров с 1+20 частицами H2O, можно увидеть еще тройное число 24-вершинников из тех же H2O. Каждый такой 24‑вершинник представляет собой 14‑гранник с 12 пятиугольными и двумя шестиугольными гранями (рис. 1.43).
Отдельно крупная молекула воды, точнее агрегат молекул H2O, с тетраэдрической симметрией в виде полиэдра с 28 вершинами и 16 гранями, из которых 12 – это пентагоны, а 4 – гексагоны, представлена на рис. 1.44.
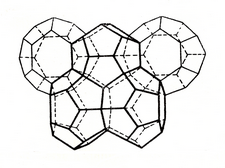
Рисунок 1.43 – Две формы больших молекулярных водных агрегатов в гидрате хлора: 12-гранники с 20 вершинами и 24-гранники с 14 вершинами
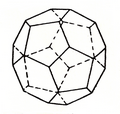
Рисунок 1.44 – Крупный молекулярный агрегат воды
Заметим, что структуры такого типа были описаны академиком Н.В. Беловым еще в середине прошлого века, в конце которого аналогичные структуры были обнаружены для углерода и известны в настоящее время под названием фуллеренов.