- •Содержание
- •Введение
- •Глава 1 особенности структуры и технологии наноразмерных объектов
- •1.1 Классификация вещественных объектов
- •1.1.1 Размерные классы частиц
- •1.1.2 Факторы, влияющие на свойства вещества
- •Риcунок 1.11 – Схема возникновения н-центра окраски в цгк типа NaCl
- •1.2 Методы получения низкоразмерных частиц
- •1.3 Модельные представления о структуре и габитусе наноразмерных частиц
- •1.3.1 Методологические подходы к описанию кристаллов
- •1.3.2 Правильные формы кристаллов и их описание
- •Общие простые формы кристаллов и кристаллографические индексы их граней (hkl)
- •Частные простые формы (грань (h 0 0))
- •Частные простые формы кристаллов с единичным направлением (исходная грань (h k 0)).
- •Частные простые формы кристаллов без единичного направления
- •1.3.3 Габитус наночастиц, полученных при диспергировании крупных кристаллов
- •1.4 Теоретическое описание структуры и габитуса наночастиц, полученных конденсированием
- •1.4.1 Шаровые упаковки как модели многоатомных структур
- •1.4.2 Атомные координации в полиэдрах плотнейших атомных упаковок
- •Радиусы координационных сфер и их числа заполнения для гцк-структур
- •Радиусы координационных сфер и их числа заполнения для гпу-структур
- •Радиусы координационных сфер и их числа заполнения для оцк-структур
- •1.4.3 Некристаллографическая симметрия габитуса наноразмерных атомных координационных полиэдров
- •1.4.4 Фуллереноподобные формы нанокристаллов
- •1.4.5 Габитусы наночастиц сложного состава
- •1.5 Структура и свойства наноразмерных частиц, применяемых в функциональном материаловедении
- •1.5.1 Структура и свойства наноразмерных металлических модификаторов функциональных материалов
- •Координационные числа (к) координационных сфер (n – ее номер) при плотнейшей шаровой упаковке
- •Основные параметры, необходимые для описания жидких кластеров металлов (z – порядковый номер, n – плотность атомов, ef – энергия Ферми, rw – радиус Вагнера-Зейтца, w – работа выхода)
- •1.5.2 Наноразмерные углеродсодержащие модификаторы*
- •Размеры кристаллических блоков в алмазосодержащих продуктах детонационного синтеза
- •Р исунок 1.66 – Термограммы tg (а) и dta (б) углеродных нанокластеров. Скорость нагрева 5оС/мин: 1 – удаг; 2 – уда
- •Фазовый состав наномодификаторов, полученных по технологии термолиза прекурсора в технологической среде
- •Характеристики модифицированных углеродных волокон [161]
- •1.5.3 Силикатные наноразмерные частицы
- •Кристаллографические индексы рефлексов (kl) и структурные амплитуды f(20) и f(850) кристалла мусковита при 20оС и после прогрева при 850оС соответственно
- •Характеристики ультрадисперсных керамик (ук), полученных плазмохимическим синтезом [179]
- •Характеристики ультрадисперсных керамик (ук) механохимического синтеза [177]
- •Характеристики ультрадисперсных оксинитридов плазмохимического синтеза [179-180]
- •Некоторые свойства природных и синтетических цеолитов
- •1.6 Заключение к главе 1
- •Глава 2 механизмы модифицирующего действия наноразмерных частиц в полимерных и олигомерных матрицах
- •2.1 Критерии оценки наноразмерности
- •2.1.1 Физические предпосылки к оценке наноразмерности частиц
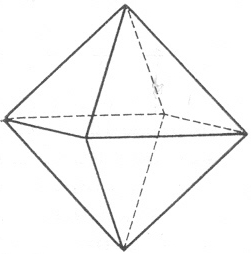
- •2.1.2 Связь фононных характеристик с наноразмерностью
- •2.1.3 Теорема Блоха и наноразмерность
- •2.1.4 Дебаевская длина волны и максимальный наноразмер
- •2.1.5 Расчет максимального наноразмера на основании уравнения Шредингера
- •2.1.6 Определение предельных размеров частиц веществ с неразрушенными полимерными молекулами
- •2.1.7 Динамические модели кристалла Эйнштейна и Дебая
- •2.1.8 Расчетные значения максимальных размеров наночастиц одноэлементных веществ и некоторых соединений
- •Характеристические температуры ( ) и максимальные размерынанокристаллов некоторых веществ
- •Характеристические температуры и максимальные размеры нанокристаллов некоторых галогенидов
- •Температура Дебая и максимальный наноразмер полупроводников типов
- •Отношение температуры Дебая наночастиц к для объемной фазы некоторых металлов, r – размер частицы
- •Дебаевская температура и наноразмерный максимум одноэлементных веществ
- •2.1.9 Влияние размеров кристаллитов на их физические свойства
- •2.2 Особенности зарядового состояния наноразмерных частиц
- •2.2.1 Зарядовое состояние дисперсных частиц слоистых минералов
- •2.3 Зарядовое состояние металлических компонентов функциональных материалов и металлополимерных систем
- •2.3.1 Модельные представления о механизме модифицирования полимерных матриц нанокомпозиционными частицами
- •Зависимость размеров областей когерентного рассеяния (l ǻ) от массовой концентрации (с, мас.%) ультрадисперсного углерода (шихты)
- •Значения радиусов (r, ǻ) и относительных координационных чисел (окч) для композитов с различной массовой концентрацией (с, мас.%) наполнителя
- •2.4 Заключение к главе 2
Частные простые формы (грань (h 0 0))
№ фор-мы |
Группа |
Число граней |
Много-гранник |
Индексы граней |
См.№1 |
1, m |
1 |
моноэдр
|
(h 0 0)
|
См.№2 |
2, ,2/m,mm2, 222,mmm |
2 |
пинакоид |
( h 0 0) |
33 |
3 |
3 |
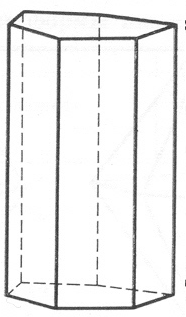
тригона-льная призма |
( |
34 |
4,4/m, 4mm, 422, 4/mmm,
|
4 |
тетраго-нальная призма |
( h 0 0 ) |
35 |
6,
6mm, 32, 622, m, 6/mmm,
|
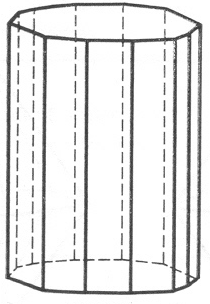
6 |
гексаго-нальная призма |
(
|
Для тригональных кристаллов в табл. 1.3
и 1.4 приведена только гексагональная
установка осей:
![]() .
Получить индексы граней чистых правильных
форм тригональных кристаллов при R
– установке координационных осей можно
на основании табл. 1.2, взяв за исходную
грань (hhh).
.
Получить индексы граней чистых правильных
форм тригональных кристаллов при R
– установке координационных осей можно
на основании табл. 1.2, взяв за исходную
грань (hhh).
При исходной плоскости (h
h l)
в зависимости от величины индексов h
и l полиэдры, изображающие
простую форму кубических кристаллов
имеют разный вид, хотя индексы граней
формы одинаковы. Различие полиэдров
при исходной плоскости (h
k l)
для случаев
![]() можно доказать, анализируя грани форм,
приведенных в табл. 1.5 (см. № 44-47).
можно доказать, анализируя грани форм,
приведенных в табл. 1.5 (см. № 44-47).
Таблица 1.4
Частные простые формы кристаллов с единичным направлением (исходная грань (h k 0)).
№ фор-мы |
Группа |
Число граней |
Много-гранник |
Индексы граней |
См.№1 |
1, m |
1 |
моноэдр |
(h k 0) |
См.№2 |
2, , 2/m, mmm, mm2 |
2 |
пинакоид |
(hk0) |
См.№33 |
3, , |
3 |
тригональ-ная призма |
( h k i 0 ) |
См.№34 |
4, 4/m, |
4 |
тетрагональ-ная призма |
|
См.№35 |
6, , 6/m |
6 |
гексагона-льная призма |
( hki 0) |
36 |
32,3m,
|
6 |
дитригона-льная призма |
({hki}0) |
37 |
4mm, 422,
4/mmm,
|
8 |
дитетраго-нальная призма |
|
38 |
6mm, 622,
|
12 |
дигексаго-нальная призма |
( h k i 0 ) и ( h i k 0 ) |
Таблица 1.5
Частные простые формы кристаллов без единичного направления
№ фор-мы |
Индексы исходной плоскости |
Группа |
Число граней |
Много-гранник |
Индексы граней |
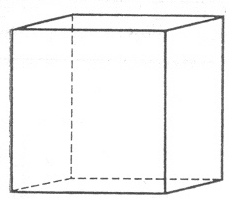
39 |
(h 0 0) |
23, m3,
|
6 |
куб |
|
40 |
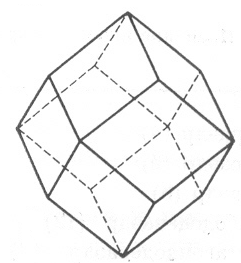
(h h 0) |
23, m3, , m3m |
12 |
ромбодо-декаэдр |
|
41 |
(h 0 0) |
23,m3 |
12 |
пентагон-додекаэдр |
|
42 |
(hk0) |
432, m3m |
24 |
тетрагек-саэдр |
|
43 |
(hhh) |
23,
|
4 |
тетраэдр |
|
44 |
(hhh) |
m3, 432, m3m |
8 |
октаэдр |
|
45 |
(hhl) h<1 |
23,
|
12 |
тригонтри-тетраэдр |
|
46 |
(hhl) h>1 |
23,
|
12 |
тетрагон- тритетраэдр |
|
47 |
(hhl) h<1 |
m3, 432, m3m |
24 |
тригон- триоктаэдр |
|
48 |
(hhl) h>1 |
m3, 432, m3m |
24 |
тетрагон- триоктаэдр |
|
Рассмотрим фигуру, полученную при
сечении полиэдров, соответствующих
простым формам кристаллов без единичного
направления, координатной плоскость,
например, Z=0. Легко
убедиться, что при
![]() в сечении лежит дитерагон, а при
в сечении лежит дитерагон, а при
![]() - тетрагон. Очевидно, что это может
выполняться лишь при различии полиэдров
для условий
- тетрагон. Очевидно, что это может
выполняться лишь при различии полиэдров
для условий
![]() .
.
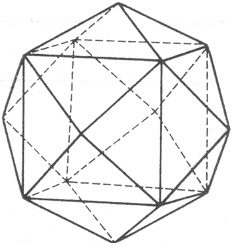
Монокристаллы с различными размерами
не обязательно ограняются плоскостями
одной формы. Например, для группы m3,
432, m3m возможно сочетание граней
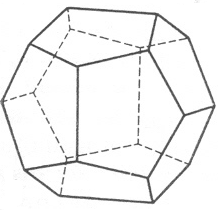
октаэдра и граней куба. Кристалл имеет
форму кубоктаэдра, которая не является
простой, ибо ее грани образуют два
семейства симметрично связанных друг
с другом плоскостей. Грани кубоктаэдра
имеют индексы
![]() ,
где k и h
принимают произвольные значения, но
так, чтобы грани октаэдра и куба не
пересекались.
,
где k и h
принимают произвольные значения, но
так, чтобы грани октаэдра и куба не
пересекались.