13.4. Операции с элементами линейного пространства в координатном представлении

Определение. Коэффициенты разложения называются координатами (или компонентами) элемента x линейного пространства 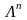в базисе .

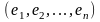Элемент линейного пространства в базисе однозначно представляется n-компонентным столбцом, называемым координатным представлением элемента в базисе :

.

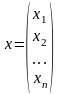В базис может быть выбран не единственным способом и потому необходимо установить правило изменения координат элемента линейного пространства при переходе от одного базиса к другому.

Пусть в даны два базиса: “старый” и “новый” 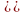с соответствующими координатными разложениями элемента x:

и .

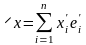Пусть, кроме того, известны разложения элементов “нового” базиса по элементам “старого”:

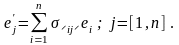(13.1)

Определение. Матрица S, j-й столбец которой состоит из коэффициентов 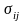координатных разложений элементов “нового” базиса по элементам “старого”, называется матрицей перехода от базиса к базису .

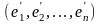Теорема 13.7 Координаты и 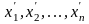связаны соотношениями

,

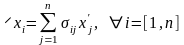называемыми формулами перехода, где коэффициенты – элементы матрицы перехода .

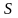Доказательство.

В силу соотношений (13.1) будут справедливы равенства

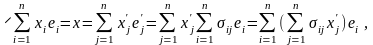
или

.

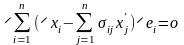Но если линейная комбинация линейно независимых (в данном случае, базисных) элементов равна нулевому элементу, то она тривиальная. Откуда получаем, что

.

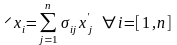Теорема доказана.

Пусть в некотором базисе

и ,

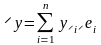тогда в силу определения базиса и аксиом линейного пространства будут справедливы следующие соотношения:

(1). Операция сравнения: два элемента в 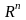равны тогда и только тогда, когда

,

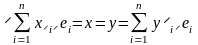или в координатной форме

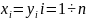
(2). Операция сложения:

,

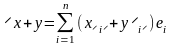или в координатной форме.

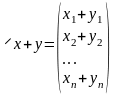
(3). Операция умножения на число:

,

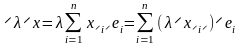или в координатной форме

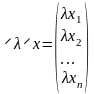
Откуда следует, что элементы конечномерного линейного пространства не только могут представляться матрицами (столбцами), но и правила выполнения операций с этими элементами совпадают с определением соответствующих матричных операций.

13.5. Изоморфизм линейных пространств

Два линейных пространства 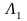и называются изоморфными, если существует взаимно однозначное отображение 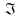: 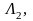 такое, что для 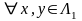и

;

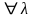
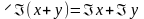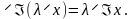
Отображение называется изоморфизмом линейных пространств и .

Напомним, что отображение является взаимно однозначным, если

а) разные элементы из имеют в разные образы;

б) каждый элемент из является образом некоторого элемента из .

Теорема 13.8 Два линейных конечномерных пространства и изоморфны тогда и только тогда, когда их размерности равны.

Доказательство.

Пусть 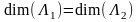. Принимая правило отображения, при котором каждому элементу 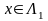ставится в соответствие элемент из , имеющий те же самые координаты, а также используя правила действий с элементами в координатном представлении, приходим к изоморфизму и .

Допустим, что 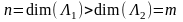, где и изоморфны. Тогда некоторый набор n линейно независимых элементов из отображается в n элементов в , которые обязаны быть линейно зависимыми. Поскольку при изоморфизме нулевой элемент переходит в нулевой элемент, то мы приходим к противоречию с предположением о линейной независимости выбранных n элементов из .

В случае 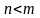аналогичные рассуждения также приводят к противоречию, и, следовательно, .

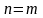Теорема доказана.