Тема 5 Ряды

Задача 1. Написать первые три члена ряда найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

Решение: Беря последовательно n=1, 2, 3, ..., запишем данный ряд в виде:

Для нахождения области сходимости ряда применим признак Даламбера

Данный ряд сходится абсолютно при тех значениях х, которые удовлетворяют неравенству <1, или |x|< , или

Исследуем сходимость ряда на концах полученного интервала.

При х= данный ряд принимает вид .

Последний ряд является знакочередующимся; абсолютная величина его общего члена стремится к нулю при . Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, х — принадлежит области сходимости данного ряда.

При х= данный ряд принимает вид . Исследуем сходимость этого ряда при помощи интегрального пpизнака сходимости Коши. Рассмотрим несобственный интеграл

Так, как несобственный интеграл сходится, то сходится и исследуемый ряд. 3начит, при х= исходный ряд сходится. Таким образом, область сходимости данного ряда.

Задача 2. Вычислить с точностью до 0,001.

Представим подынтегральную функцию в виде степенного ряда. Заменив х в разложении функции sin х на , имеем:

Тогда

Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда

Вопросы для самопроверки

1. Что называется числовым рядом?

2. Что называется n-й частичной суммой числового ряда?

3. Какой числовой ряд называется сходящимся?

4. Что является необходимым условием сходимости числового ряда?

5. Назовите достаточные признаки сходимости, основанные на сравнении рядов.

6. Назовите признак Даламбера сходимости рядов, радикальный признак сходимости Коши?

7. В чем состоит интегральный признак сходимости Коши?

8. Какие ряды называются знакочередующимися? Приведите примеры.

9. Сформулируйте признак Лейбница сходимости знакочередующихся рядов.

10. Какие знакочередующиеся ряды называются абсолютно сходящимися? условно сходящимися?

11. Дайте определение степенного ряда и области его сходимости.

12. Kaк найти область сходимости степенного ряда?

13. Запишите разложение в степенной ряд функций е^x, sin х, соs х, (1+x)^m, 1n 5(1+х).

14. Как обеспечивается требуемая точность при применении степенных рядов в при­ближенных вычислениях?

Задания для контрольной работы №2

Задание 1

Данную функцию z=f(x, y) исследовать на экстремум.

1. z= .

2. z= .

3. z= .

4. z=

5. z= .

6. z= .

7. z= .

8. z= .

9. z= .

10. z= .

11. z= .

12. z= .

13. z= .

14. z= .

15. z= .

16. z= .

17. z= .

18. z=

19. z= .

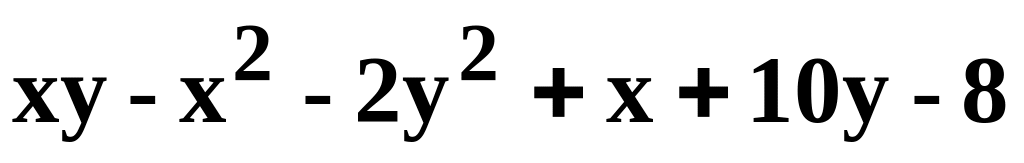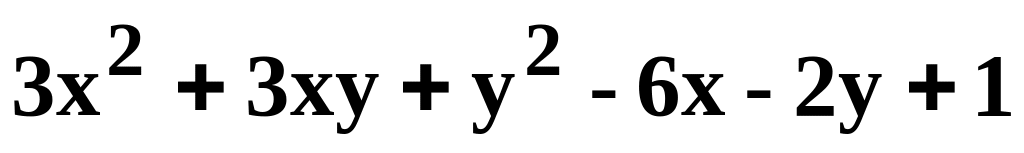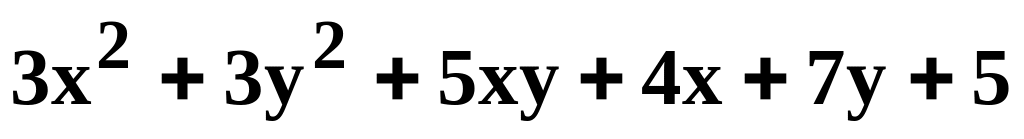
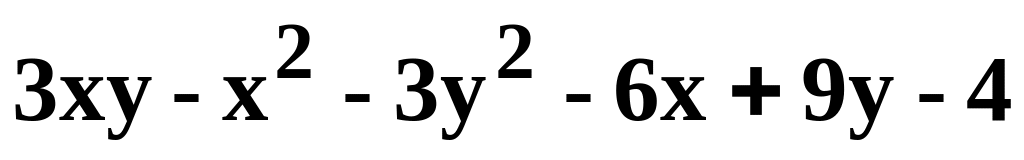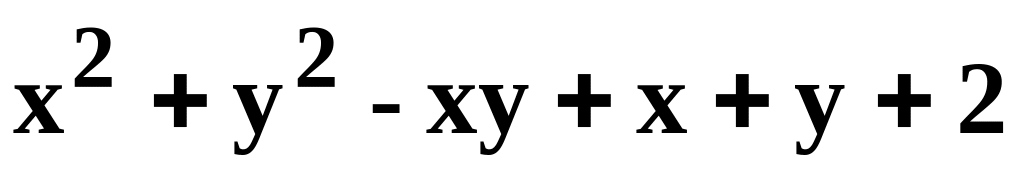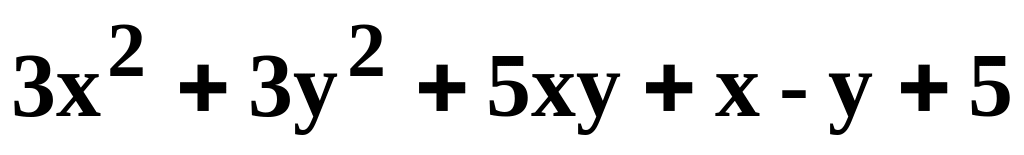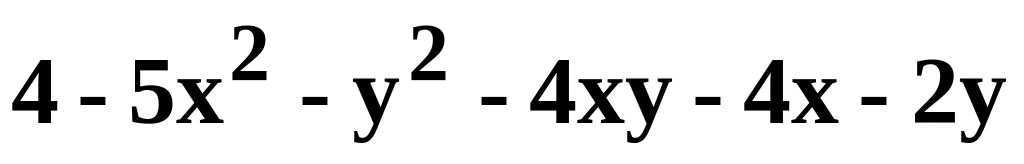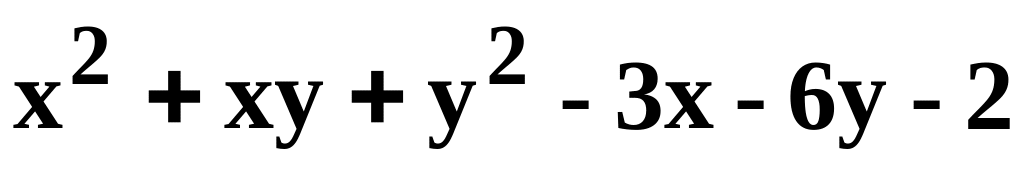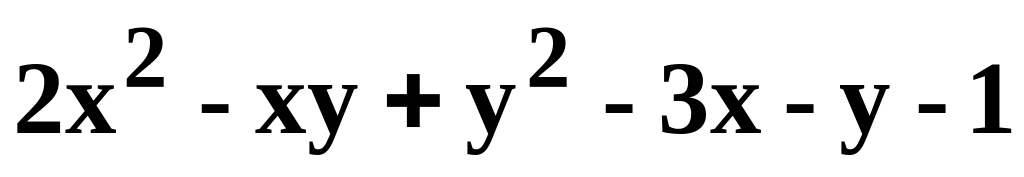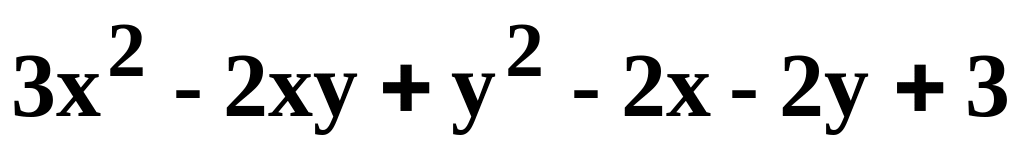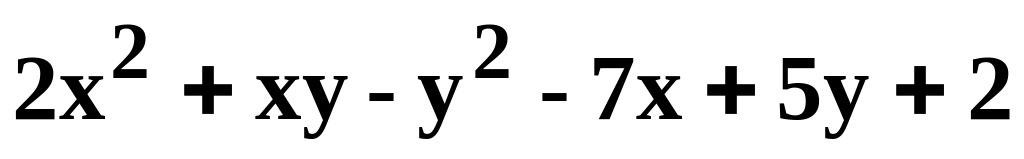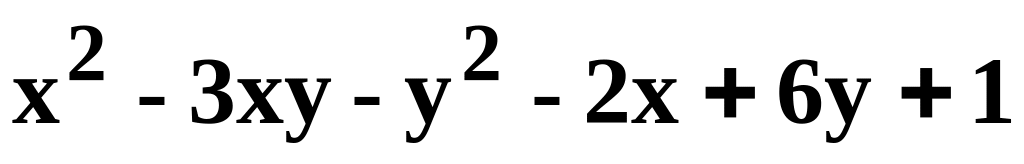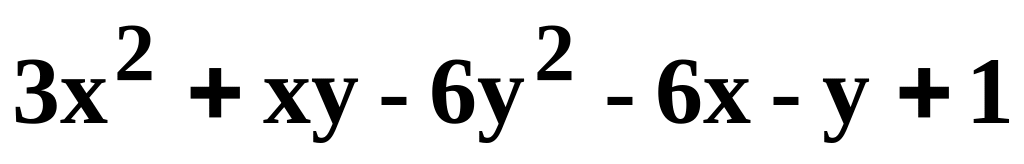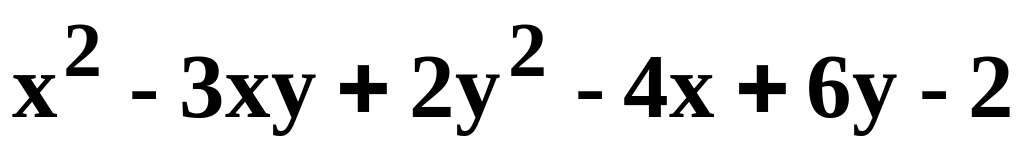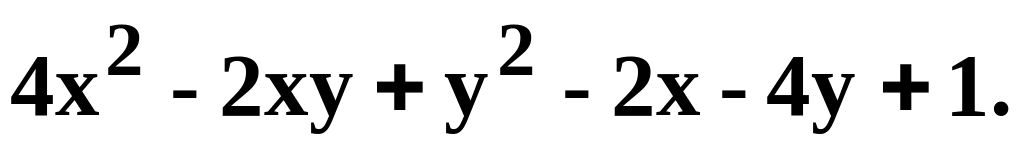
20. z= .

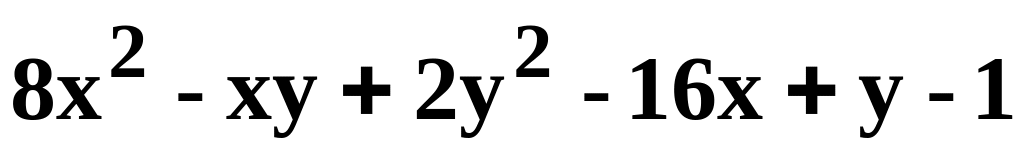Задание 2

В задачах 1 – 20 найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием.

1. а) б) в)

2. а) б) в)

3. а) б) в)

4. а) б) в)

5. а) б) ; в)

6. а) б) в) .

7. а) б) в)

8. а) б) в)

9. а) б) в)

10. а) б) в)

11. а) б) в)

12.а) б) в)

13. а) б) в)

14. а) б) в)

15. а) б) в)

16. а) б) в)

17. а) б) в)

18. а) б) в)

19. а) б) в)

20. а) б) в)

Задание 3

В задачах 1 – 10 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.

1. у = х³; у = 2. у = у = 6 – х .

3. у = у = 4 – х . 4. у = х²+2; у = 4 – х².

5. у = - х²+1; у = х – 1. 6. у = x² – 4x+4; y=x.

7. y = y = 4x. 8. y = y = 7 – x.

9. y = 3x²+1; y = 3x+7. 10. y = 2x – x²; y = - x.

В задачах 11 – 15 вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж.

11. y² = x; y = x². 12. xy = 4; x = 1; x = 4; y = 0.

13.y = sin x (одна полуволна); y = 0. 14. y = x²+1; y = 3x – 1.

15.

В задачах 16 – 20 вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной указанными линиями. Сделать чертеж.

16. y² =4 – x ; x=0. 17.

18. x + y – 2 =0; x=0; y=0. 19. xy =2; x=0; y=1; y=4.

20. y =-x²+4; x=0; y=0; y=3.

Задание 4

В задачах 1 – 20 найти общее решение дифференциальных уравнений первого порядка.

1. (e^2x+1)dy+ye^2xdx=0. 2. (2+y) dx – (2 – x ) dy =0.

3. x²dy+(y – 1)dx =0. 4. y (e^x+1)dy – e^xdx =0.

5. (e^x+2)y^/ =ye^x. 6. y^/ =e^{x – y} .

7. xyy^/ = 3x². 8. y^/ tg x – y =0.

9. (1+x²)y^/ = 1+y². 10. y^/ cos x – y sin x=0.

11. xy^/ - y =x³. 12. xy^/ - y = – 2lnx.

13. x³y^/ +3x²y =2. 14. y^/ + e^x y =e^2x.

15. xy^/ + y = x+1. 16. y^/ – y cosx = – sin 2x.

17. xy^/ – y = -ln x. 18. y^/ – 4xy = -4x³.

19. 2xy^/ + y = 2x³ . 20. y^/ + xy = –x³.

Задание 5

В задачах 1 – 20 найти общее решение дифференциального уравнения.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

Задание 6

В задачах 1 – 20 найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.

1.y′′+y′-2y=6x2,y(0)=-4,y′(0)=–1.

2. y′′–4y =8x3, y(0) = 2, y′(0) = – 3.

3. y′′– 2y′ +y =8ex, y(0) = 1, y′ (0) =3.

4. y′′+ 2y′+5y = 4e-x, y(0) = 1, y′ (0) -1.

5. y′′+6y′+9y = 10 sin x, y(0)=0, y′(0) =1.

6. y′′+9y = cos 3x, y(0) =1, y′ (0) =3.

7. y′′– 3y′ +2y =ex, y(0) =2, y′(0) = 2.

8. y′′– 5y′ + 6y = 13 sin 3x, y(0) = 2, y′ (0)=2.

9. y′′– 2y′ = 2x+1, y(0) =1, y′(0) =1.

10. y′′+ y =2x3– x+2, y(0) =3, y′(0) = – 2.

11. y′′+y′-2y=6x2,y(0)=-4,y′(0)=–1.

12. y′′–4y =8x3, y(0) = 2, y′(0) = – 3.

13. y′′– 2y′ +y =8ex, y(0) = 1, y′ (0) =3.

14. y′′+ 2y′+5y = 4e-x, y(0) = 1, y′ (0) -1.

15. y′′+6y′+9y = 10 sin x, y(0)=0, y′(0) =1.

16. y′′+9y = cos 3x, y(0) =1, y′ (0) =3.

17. y′′– 3y′ +2y =ex, y(0) =2, y′(0) = 2.

18. y′′– 5y′ + 6y = 13 sin 3x, y(0) = 2, y′ (0)=2.

19. y′′– 2y′ = 2x+1, y(0) =1, y′(0) =1.

20. y′′+ y =2x3– x+2, y(0) =3, y′(0) = – 2.

Задание 7

В задачах 1 – 20 дан степенной ряд

При заданных значениях а и b написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

1. a=2, b=3. 2. a=3, b= 5. 3. a=4, b=7. 4. a=5, b=9.

5. a=7, b=6. 6. a=2, b=5. 7. a=3, b=2. 8. a=4, b=3.

9. a=5, b=2. 10. a=6, b=4. 11. a=3, b=7. 12. a=4, b=5.

13. a=8, b=3. 14. a=7, b=4. 15. a=5, b=7. 16. a=2, b=6.

17. a=3, b=4. 18. a=7, b=5. 19. a=5, b=8. 20. a=2, b=4.

Задание 8

В задачах 1 – 20 вычислить определенный интеграл с точностью до 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

1. 2. 3. 4.

5. 6. 7. 8.

9. 10. 11. 12.

13. 14. 15. 16.

17. 18. 19. 20.

Литература

1. Шипачев В.С.

Курс высшей математики: учебник для вузов /В.С.Шипачев; Под редакцией А.Н. Тихонова. – 3-е изд., испр. – М.: Издательство Оникс, 2007 – 600с.: ил.

2. Демидович Б.П.

Краткий курс высшей математики: учеб. пособие для вузов / Б.П. Демидович, В.А. Кудрявцев. – М.:ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003 – 654, [2] с.: ил.

3. Шипачев В.С.

Задачник по высшей математике: учеб. пособие для студ. вузов/ В.С. Шипачев- 6-е изд., стер..- М.: Высш. шк., 2006.- 304 с.

Дополнительная литература

1. Данко П.Е.

Высшая математика в упражнениях и задачах: учеб. пособие: в 2 ч./П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд..- М.: ОНИКС 21 век : Мир и образование. – 2003.- Ч.1.- 2003. - 304 с.

2. Данко П.Е.

Высшая математика в упражнениях и задачах: учеб. пособие: в 2 ч./П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд..- М.: ОНИКС 21 век : Мир и образование. – 2003.- Ч.2.- 2003. - 416 с.

3. Письменный Д.Т.

Конспект лекций по высшей математике. I, II ч. – М.: Рольф, 2007. – 603 с.

0