Описание и теория метода

Предлагаемый метод определения  основан на применении уравнений адиабатического и изохорического процессов.

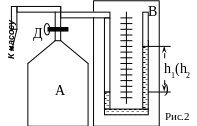Установка состоит из стеклянного баллона А, соединенного с манометром В и насосом (рис.2). Посредством крана Д баллон может быть соединен с атмосферой, и будем считать, что первоначально в нем было атмосферное давление. Если с помощью насоса накачать в баллон некоторое количество воздуха и закрыть кран, то давление в баллоне повысится; но если это повышение было произведено достаточно быстро, то манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, температура его повысится. Окончательная разность уровней в манометре h установится только тогда, когда температура воздуха внутри баллона сравняется, благодаря теплопроводности стенок, с температурой окружающего воздуха.

Обозначим через Т₁ термодинамическую температуру окружающего воздуха и через р₁ - давление газа внутри сосуда, соответствующее показанию манометра h₁. Очевидно, давление, установившееся в баллоне, будет равно (15)

где р₀ - атмосферное давление (конечно, при этом р₀ и h₁ должны быть выражены в одинаковых единицах). Эти два параметра Т₁ и р₁ характеризуют состояние газа, которое мы назовем первым состоянием газа.

Если теперь быстро открыть кран, то воздух в баллоне будет расширяться адиабатически, пока давление его не сделается равным р₀; при этом он охладится до температуры Т₂. Это будет второе состояние газа: Т₂ и р₀.

Если сразу после открывания снова закрыть кран, то давление внутри баллона начнет возрастать вследствие того, что охладившийся при расширении воздух в баллоне станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в баллоне сравняется с внешней температурой Т₁. Обозначим давление воздуха в баллоне в этот момент через р₂ и соответствующее показание манометра - через h₂. Это будет третье состояние газа: Т₁ и р₂. Ясно, что (16) Так как переход от второго состояния (после закрытия крана) к третьему произошел без изменения объема, то можно применить здесь закон Гей-Люссака: (17)

К переходу из первого состояния во второе (процесс адиабатического расширения) применяем уравнение Пуассона в форме: 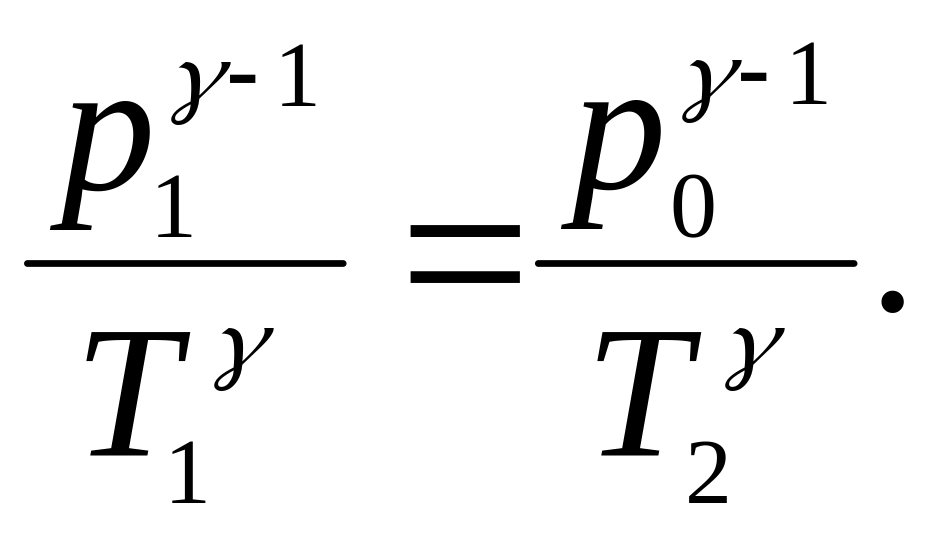(18)

Эта форма уравнения Пуассона может быть легко получена из обычной (13) если воспользоваться для этой цели уравнением состояния газа Возводя последнее уравнение в степень  и разделив его почленно на уравнение Пуассона, получим: 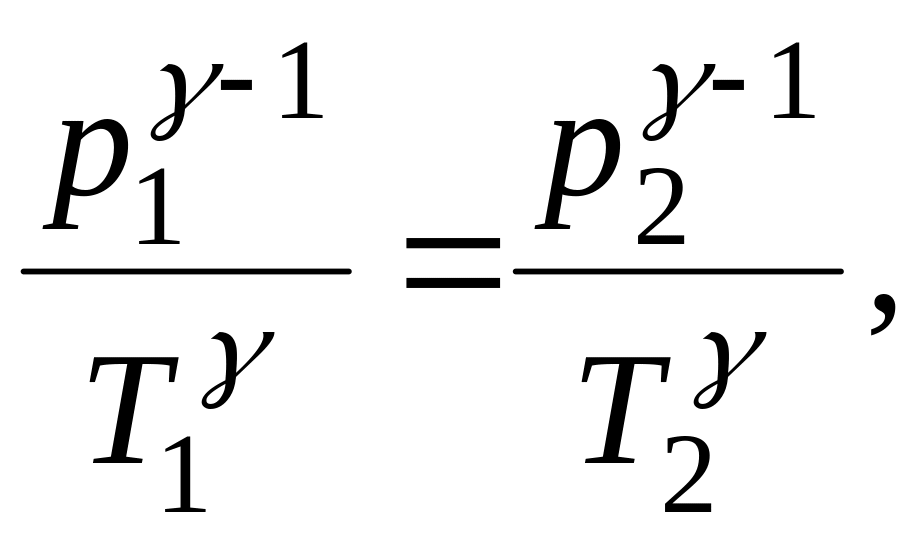т.е. уравнение, аналогичное (18).

Подставляя в уравнение (18) значение р₁ из (15) и переставляя члены, получаем:

Разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получаем:

откуда

Но выражение, стоящее в левой части этого уравнения, есть не что иное, как h₂; действительно, подставив в уравнение ( 17) значение р₁ из уравнения (16) и разрешив его относительно h₂, получим:

Следовательно, можно записать: откуда окончательно находим: (19)