
- •Практикум по механике и молекулярной физике
- •Содержание
- •10. Определение модуля сдвига из крутильных колебаний……….………..62
- •11. Определение коэффициента вязкости жидкости по методу Стокса……66
- •1.1. Правила работы в лаборатории, оформление результатов работы
- •Правила работы в лаборатории
- •Оформление отчетов
- •Графики
- •1.2. Обработка результатов физического эксперимента
- •Вычисление погрешностей прямых измерений
- •Погрешности косвенных измерений
- •1.3. Изучение измерительных приборов Нониусы
- •Ш тангенциркуль
- •Микрометр
- •1.4. Определение плотности твердых тел, имеющих правильную геометрическую форму
- •2. Гармонические колебания
- •Математический маятник
- •Физический маятник
- •Выполнение работы
- •Упражнение 2. Определение ускорения свободного падения при помощи оборотного маятника.
- •Работа n 2-2
- •Контрольные вопросы
- •3. Затухающие колебания
- •Работа № 3-1 определение логарифмического декремента затухания и коэффициента затухания крутильных колебаний
- •Описание прибора
- •Выполнение работы
- •Определение логарифмического декремента затухания и коэффициента затухания колебаний математического маятника
- •Контрольные вопросы.
- •Работа № 4 изучение законов динамики поступательного движения с помощью машины атвуда
- •К раткая теория
- •Описание установки и метода измерений
- •Выполнение работы
- •Контрольные вопросы
- •5. Кинематика и динамика вращательного движения
- •2. Момент силы и момент инерции
- •Работа № 5-1 определение моментов инерции твердых тел при помощи крутильных колебаний
- •Описание установки Общий вид крутильного маятника показан на рис. 1.Крутильный
- •Описание метода определения моментов инерции твердых тел.
- •Тогда период колебаний т будет равен: . (5)
- •Очевидно, что период колебания рамки с исследуемым телом
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 5-2 определение моментов инерции твердых тел с помощью маятника максвелла
- •Описание установки и метода измерений
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 5-3 Определение момента инерции тел с помощью трифилярного подвеса
- •О писание установки и метода определения момента инерции тел
- •Выполнение работы
- •Определение момента инерции j ненагруженной платформы
- •Определение момента инерции твердого тела
- •Изучение зависимости момента инерции системы (платформа плюс тело) от расположения тела на платформе
- •Контрольные вопросы
- •Работа № 5-4 исследование вращательного движения твердых тел с помощью маятника обербека.
- •Выполнение работы.
- •Выполнение работы.
- •Описание установки
- •Выполнение рабаты
- •Контрольные вопросы
- •Работа № 8
- •Краткая теория
- •Описание установки
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 9 определение модуля юнга методом прогиба
- •Краткая теория
- •Описание установки
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 10 определение модуля сдвига из крутильных колебаний
- •Краткая теория
- •Описание установки и вывод расчетной формулы
- •Выполнение работы
- •Краткая теория
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 12 определение отношения удельных теплоемкостей газов методом клемана-дезорма
- •Краткая теория
- •Описание и теория метода
- •Выполнение работы
- •Контрольные вопросы
- •Работа № 13 определение скорости звука в воздухе и отношение удельных теплоемкостей ср/сv для воздуха методом стоячих звуковых волн
- •Подставляя (15) в (13), находим, что (16)
- •Описание установки
- •Выполнение работы
- •Контрольные вопросы
- •Работа №14 определение коэффициента поверхностного натяженияжидкости методом компенсации дополнительного давления
- •Краткая теория
- •Описание установки и вывод расчетной формулы
- •Выполнение работы Задание 1. Измерение диаметра капилляра
- •Задание 2. Определение коэффициента поверхностного натяжения жидкости
Контрольные вопросы
1.Объясните механизм внутреннего трения в жидкостях
Объясните физический смысл коэффициента вязкости.
В каких единицах измеряется коэффициент вязкости в ед.СИ и системе СГС?
Выведите рабочую формулу (6), поясните этот вывод.
Как зависит коэффициент вязкости от температуры?
Что представляет собой градиент скорости? Дайте определение этой величины.
Работа № 12 определение отношения удельных теплоемкостей газов методом клемана-дезорма
Приборы и принадлежности: стеклянный баллон с трехходовым краном, манометр, воздушный насос.
Краткая теория
Опыт
показывает, что количество теплоты![]() ,
необходимое для нагревания массы
однородного вещества от температуры
Т1
до Т2
градусов, пропорционально массе вещества
и изменению температуры:
,
необходимое для нагревания массы
однородного вещества от температуры
Т1
до Т2
градусов, пропорционально массе вещества
и изменению температуры:
= cm(T2-T1), (1)
где с - удельная теплоемкость вещества. Из формулы (1) следует
![]() (2)
(2)
Отсюда видно, что удельной теплоемкостью называется количество теплоты, необходимое для нагревания вещества массой 1 кг на 1 К.
Положив
m=1
кг,
=
1 Дж,
![]() ,
получим единицу удельной теплоемкости:
,
получим единицу удельной теплоемкости:
![]()
Кроме удельной теплоемкости вещества вводится понятие молярной теплоемкости С. Молярной теплоемкостью называется количество теплоты, необходимое для нагревания моля вещества на 1 К. Из определения удельной теплоемкости следует, что она связана с молярной соотношением
![]() ,
(3)
,
(3)
где μ- молярная масса вещества. Единицей С является Дж/(мольК).
Состояние газа может быть охарактеризовано тремя величинами - параметрами состояния: давлением p, объемом V и температурой T. Уравнение, связывающее эти величины, называется уравнением состояния вещества. Для случая идеального газа уравнением состояния является уравнение Менделеева-Клапейрона, которое для одного моля газа будет иметь вид pV = RT (4)
где R - универсальная газовая постоянная.
Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись уравнением состояния (4) и первым началом термодинамики, которое можно сформулировать следующим образом:
количество
теплоты
![]() ,
переданное системе, затрачивается на
увеличение ее внутренней энергии
,
переданное системе, затрачивается на
увеличение ее внутренней энергии
![]() и на работу
и на работу
![]() ,
совершаемую системой против внешних
сил
,
совершаемую системой против внешних
сил
![]() .
(5)
.
(5)
По
определению теплоемкости
![]() (6)
(6)
Из
уравнения (6) видно, что теплоемкость
может иметь различные значения в
зависимости от способов нагревания
газа, так как одному и тому же значению
![]() могут соответствовать различные значения
и
.
Элементарная работа
равна
могут соответствовать различные значения
и
.
Элементарная работа
равна
![]() .
.
Внутренняя
энергия 1 моля газа
![]() ,
(7),
,
(7),
где i- число степеней свободы.
Числом степеней свободы газа называется число независимых координат, определяющих положение тела в пространстве.
При движении точки по прямой линии для оценки ее положения надо знать одну координату, т.е. точка имеет одну степень свободы. Если точка движется по плоскости, ее положение характеризуется двумя координатами, т.е. точка обладает двумя степенями свободы. Положение материальной точки в пространстве определяется тремя координатами.
 Число
степеней свободы молекулы обычно
обозначается буквой
i-.
Молекулы, которые состоят из одного
атома, считаются материальными точками
и имеют число степеней свободы i-
=3. Такими являются молекулы аргона,
гелия и др. Двухатомные молекулы (H2,
N2
и др.) обладают числом степеней свободы
i=5;
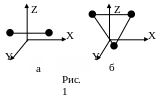
они имеют три степени свободы
поступательного движения вдоль осей
X,
Y,
Z
и две степени свободы вращения вокруг
осей X
и Z
(рис.1, а). Вращением вокруг оси Y
можно пренебречь, т.к. момент инерции
ее относительно этой оси очень мал.
Молекулы, состоящие из трех и более
жестко связанных атомов, не лежащих на
одной прямой (рис.1, б), имеют число
степеней свободы i
= 6: три степени свободы поступательного
движения и три степени свободы вращения
вокруг осей X,
Y,
Z.
Столько же степеней свободы имеют и
другие многоатомные молекулы.
Число
степеней свободы молекулы обычно
обозначается буквой
i-.
Молекулы, которые состоят из одного
атома, считаются материальными точками
и имеют число степеней свободы i-
=3. Такими являются молекулы аргона,
гелия и др. Двухатомные молекулы (H2,
N2
и др.) обладают числом степеней свободы
i=5;
они имеют три степени свободы
поступательного движения вдоль осей
X,
Y,
Z
и две степени свободы вращения вокруг
осей X
и Z
(рис.1, а). Вращением вокруг оси Y
можно пренебречь, т.к. момент инерции
ее относительно этой оси очень мал.
Молекулы, состоящие из трех и более
жестко связанных атомов, не лежащих на
одной прямой (рис.1, б), имеют число
степеней свободы i
= 6: три степени свободы поступательного
движения и три степени свободы вращения
вокруг осей X,
Y,
Z.
Столько же степеней свободы имеют и
другие многоатомные молекулы.
Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равна одному молю. Количество теплоты, необходимое для нагревания одного моля газа на 1К, определяется молярной теплоемкостью.
Изохорический
процесс.
Процесс называется изохорическим, если
объем тела при изменении температуры
остается постоянным, т.е. V=const.
В этом случае:
![]() .
Следовательно, и
.
Следовательно, и
![]() ,
т.е. при этом вся подводимая к газу
теплота идет на увеличение его внутренней
энергии. Тогда из уравнения (6) следует,
что молярная теплоемкость газа при
постоянном объеме равна
,
т.е. при этом вся подводимая к газу
теплота идет на увеличение его внутренней
энергии. Тогда из уравнения (6) следует,
что молярная теплоемкость газа при
постоянном объеме равна
![]() .
(8)
.
(8)
Изобарический
процесс.
Процесс, протекающий при постоянном
давлении (P=const),
называется изобарическим. Для этого
случая формула (6) перепишется в виде:
![]() .
(9)
.
(9)
Из уравнения газового состояния (4) получаем:
![]() .
(10)
.
(10)
Но
Р=const
и dР=0.
Следовательно,
![]() . Подставляя это выражение в уравнение
(9), получим
. Подставляя это выражение в уравнение
(9), получим
![]() .
(11)
.
(11)
Сравнив
(8) и (11), получим
![]() .
(12)
.
(12)
Изотермический
процесс.
Изотермическим процессом называется
процесс, протекающий при постоянной
температуре (T=const).
В этом случае
![]() и
и
![]() ,
т.е. внутренняя энергия газа остается
постоянной и все подводимое тепло
расходуется на работу.
,
т.е. внутренняя энергия газа остается
постоянной и все подводимое тепло
расходуется на работу.
Адиабатический
процесс.
Процесс, протекающий без теплообмена
с окружающей средой, называется
адиабатическим. Первое начало термодинамики
для такого процесса будет иметь вид
![]() :
:
![]()
т.е. при адиабатическом процессе расширения или сжатия, работа совершается газом только за счет изменения запаса внутренней энергии.
Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии
![]()
Но
![]() и
и
![]() ,
значит,
,
значит,
![]()
Разделив уравнение (10) на (12) и учитывая (12), получим
![]()
где
![]() называется отношением удельных
теплоемкостей
называется отношением удельных
теплоемкостей
Интегрируя и потенцируя, получим уравнение Пуассона:
![]() (13)
(13)
Используя формулы (11) и (12), для γ можно получить:
![]() (14)
(14)
Эта формула справедлива как для молярных, так и для удельных теплоемкостей газов. Таким образом, по значениям теплоемкостей все газы можно разделить на три сорта: одноатомные, двухатомные, многоатомные газы.
