Контрольные вопросы

1. Сформулируйте и запишите закон Гука.

2. Запишите и объясните формулу закона Гука для деформаций растяжения и сдвига.

3. В чем физический смысл модуля Юнга и коэффициента Пуассона?

4. Объясните зависимость модуля Юнга от природы вещества и температуры.

Работа № 10 определение модуля сдвига из крутильных колебаний

Принадлежности: прибор для определения модуля сдвига из крутильных колебаний, секундомер, микрометр, масштабная линейка.

Краткая теория

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Этот вид деформации возникает под действием сил, приложенных к двум диагонально противоположным граням тела, касательным к той поверхности, на которую они действуют (рис.1).

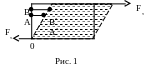Касательная сила F_, действующая на единицу поверхности, называется тангенциальным (касательным) напряжением: (1)

Измеряется тангенциальное напряжение в тех же единицах, что и давление.

Деформация сдвига характеризуется величиной относительного сдвига . Чтобы объяснить, что такое относительный сдвиг, обратимся к рис.1. Выберем какие-нибудь точки тела, лежащие на одной прямой, например, точки А и В. При деформации сдвига величины смещения выбранных точек АА^ и ВВ^ называются абсолютным сдвигом. Абсолютный сдвиг для различных точек различен (АА^  ВВ^ ), но отношение каждого этого сдвига к расстоянию до точки О будет одно и то же:

Если деформации малы, то Поэтому можно сказать, что относительный сдвиг есть измеренный в радианах угол сдвига.

По закону Гука для малых деформаций относительный сдвиг пропорционален тангенциальному напряжению, т.е. (2)

Величина G называется модулем сдвига. Таким образом, модуль сдвига численно равен тангенциальному напряжению, которое возникло бы в твердом теле при относительном сдвиге, равном единице.

В.СИ модуль сдвига измеряется в Н/м² (Па), а в системе СГС - в дин/см².

В данной лабораторной работе модуль сдвига определяется косвенно - из деформации кручения. Рассмотрим более подробно этот вид деформации и ее связь с деформацией сдвига.

Деформация кручения возникает в образце (стержне, проволоке и т.п.), если одно сечение образца закреплено неподвижно, а во втором действуют две равные по модулю и противоположные по направлению касательные силы (пара сил), момент которых относительно центра этого сечения направлен по оси образца (рис.2).

Под действием крутящего момента все поперечные сечения стержня, изображенного на рис.2, поворачиваются вокруг оси ОО^ на некоторые углы, тем большие по величине,

чем дальше эти сечения расположены от сечения, закрепленного неподвижно. Угол поворота  верхнего сечения называют углом кручения. В результате деформации кручения возникает перекос на угол  образующих цилиндрической поверхности стержня.

По закону Гука угол кручения  связан с моментом соотношением

(3)

где N - модуль кручения, который показывает, какой момент нужно приложить, чтобы закрутить стержень на угол в один радиан. Найдем теперь связь между модулем сдвига и модулем кручения. Для этого предположим, что стержень с радиусом r и длиной L из материала, модуль сдвига которого G, закручен под действием момента на угол  (см.рис.2). Это означает, что верхнее основание повернуто относительно нижнего на угол . Вырежем из стержня диск малой высоты dL и положим, что нижнее основание этого диска при закручивании повернулось на угол ^, а верхнее - на угол ^+d. Из этого диска вырежем кольцо с внутренним радиусом r и внешним r+dr (рис.3,а).

Все кубики, вырезанные из такого кольца (рис.3,в), будут иметь одинаковую деформацию сдвига на один и тот же угол . Таким образом, деформация кручения свелась к деформации сдвига. Из рис.3а видно, что

или (4)

Определим теперь упругую касательную силу, действующую на поверхность кольца, площадь которого . Согласно (1) и (2),

С другой стороны, элементарный момент dM равен

Тогда для всего стержня полный момент М равен

.

После интегрирования получим: .Очевидно, что для однородного стержня . Тогда , (5)

где Д=2r - диаметр стержня.

Подставляя (5) в (3), получим соотношение между модулем кручения N и модулем сдвига G: . (6)