2. Определение момента инерции твердого тела

Для выполнения этого упражнения необходимо на центр платформы поместить тело с произвольной массой m_т. Установка тела проверяется по расположению его относительно концентрических окружностей, нанесенных на платформе. Далее, как в п.1, определяется период колебаний системы – платформа плюс тело и рассчитывается момент инерции J_с системы по формуле: J_c= k(m_пл + m_тела)Т²,

Момент инерции тела определяется по формуле: J_тела = J_c – J_пл .По данным измерений составить таблицу, аналогичную табл. 1.

3. Изучение зависимости момента инерции системы (платформа плюс тело) от расположения тела на платформе

По диаметру платформы поместить два тела одинаковой формы и массы так, чтобы они соприкасались в центре платформы. Определить момент инерции системы по формуле: J_c= k(m_пл + m_2тел)Т²,

где m_2тел масса двух тел. Тогда момент инерции J_2Т двух тел относительно оси вращения платформы будет равен: .

Увеличив расстояние между телами, повторить опыт и сделать вывод о том, как изменяется момент инерции от положения тел на платформе.

Это упражнение можно выполнить, изменяя положение одного тела на платформе (например, параллелепипеда) из вертикального в горизонтальное и наоборот.

Контрольные вопросы

1. Что называется моментом инерции тела относительно оси вращения? В каких единицах измеряется момент инерции?

2. Может ли тело иметь несколько моментов инерции?

3. Как зависит момент инерции от распределения массы?

4. Как связаны между собой момент силы и момент инерции тела?

5. Как зависит момент силы от направления приложенной к нему силы и от расстояния от оси вращения до точки приложения силы?

Работа № 5-4 исследование вращательного движения твердых тел с помощью маятника обербека.

Приборы и принадлежности: маятник Обербека с электронным блоком управления, набор грузов.

Описание установки и метода измерений.

Маятник Обербека (рис.1) представляет собой крестовину, состоящую из четырех взаимно перпендикулярных одинаковых стержней 1, которые ввинчены в металлическую втулку 2 радиусом r. Эта крестовина свободно вращается вокруг горизонтальной оси. На стержни надеты одинаковые грузы 3 массой m' ,которые могут быть закреплены на различных расстояниях l от оси вращения. На ось вращения маятника посажены два легких шкива 4 с различными радиусами R₁ и R₂. На один из шкивов наматывается шнур к свободному концу которого, перекинутого через блок, прикрепляется платформа 5. Если на платформу поместить груз массой m, то они, падая вниз и натягивая нить, будут приводить крестовину в равноускоренное вращательное движение. Перемещая грузы m' по стержням, можно менять момент инерции маятника. Беря разные грузы m, а также шкивы разного радиуса, можно менять момент вращающей силы: M = FR , (1)

г де F-вращающая сила, R-плечо силы (в данном случае -радиус шкива).

Имеющаяся на стойке установки миллиметровая шкала позволяет измерить путь h, проходимый платформой с грузом m при их падении. На верхнем 6 и нижнем 7 кронштейнах расположены фотоэлектрические датчики. При пересечении светового луча движущимся грузом сигнал первого датчика включает электронный секундомер, а сигнал второго датчика выключает его. На индикаторе секундомера 8 высвечивается время t прохождения грузом пути h (расстояния между кронштейнами).

Ускорение a груза может быть найдено на основе закона кинематики равноускоренного движения: (2)

Зная ускорение груза, можно по второму закону Ньютона определить силу F_н натяжения нити: ma = mg - F_н,

где g- ускорение свободного падения. Тогда F_н = m (g-a) (3)

Такая же сила со стороны нити приложена по касательной к шкиву крестовины. Момент этой силы М относительно оси вращения, согласно (1), будет равен: (4)

Этот момент силы в соответствии с основным законом динамики вращательного движения M = I (5)

вызывает ускоренное вращение крестовины с угловым ускорением , (I - момент инерции крестовины относительно оси вращения). Величина  может быть определена из взаимосвязи линейного и углового ускорения:

(6)

На основании экспериментальных данных могут быть найдены:

момент силы M, действующей на крестовину, и угловое ускорение  крестовины. Это позволяет проверить справедливость основного закона динамики вращательного движения (5), линейную зависимость  от M, а также определить момент инерции I системы. При этом считается, что силой трения в подшипнике маятника и силами сопротивления, действующими на движущиеся тела, можно пренебречь.

Р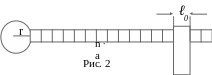 асстояние l от центра груза до оси вращения определяется (рис.2) по шкале, нанесенной на стержне, и определяется по формуле :

где r = (200,1) мм - радиус втулки,

а = (100,1) мм - цена одного деления шкалы стержня,

l₀ = (200,1) мм - размер цилиндрического груза m по его высоте.

Основные данные установки:

радиусы шкивов R₁ = (210,1) мм и R₂ = (440,1) мм; масса одного груза m = (1890,01) г; массы грузов, помещаемых на платформу, m = (410,01) г; масса платформы равна (530,01) г.