Выполнение работы

1. Подключить прибор к сети. По очереди нажать кнопки «сеть» и «сброс».

На цифровом табло должны высвечиваться нули.

2. Отклонить рамку прибора таким образом, чтобы стрелка 9 приблизилась к сердечнику электромагнита 7, который зафиксирует рамку в заданном положении. Положение электромагнита задается преподавателем.

3. Нажать кнопку «пуск». При этом освобожденная рамка начнет совершать крутильные колебания. На цифровом табло будет высвечиваться число полных колебаний n и соответствующее им время колебаний. После завершения 10-20 колебаний нажать кнопку «стоп». Записать соответствующие показания n и t. По формуле T₀ = t/n определить период колебаний ненагруженной рамки. Измерения проделать не менее трех раз и найти среднее значение T₀.

4. Поместить эталонное тело между неподвижной и подвижной балками рамки. Затягивая гайки 12 на зажимных втулках, проверить надежность крепления эталонного тела. В нашей работе в качестве эталонных тел используются сплошные металлические цилиндры, момент инерции которых относительно оси цилиндра равен , где m – масса цилиндра. Масса эталонных тел указана с точностью m=0.1 г, а геометрические размеры цилиндра измеряются штангенциркулем.

Тогда окончательная расчетная формула для определения момента инерции будет иметь следующий вид: . (10)

5. Повторяя последовательно пункты 1, 2, 3, определить период колебаний Т_эт рамки с эталонным телом.

6. Заменить в рамке эталонное тело на тело с неизвестным моментом инерции (по указанию преподавателя) и в соответствии с п. 5 определить период колебаний Т_х рамки с телом, момент инерции которого необходимо определить.

7. По формуле (10) определить неизвестный момент инерции, подставив в нее значения Т₀, Т_эт, Т_х и рассчитанное значение J_эт.

8. Определить моменты инерции того же тела относительно других осей вращения, для чего поменять положение тела в рамке и повторить пункты 6 и 7.

9. Для одного из полученных неизвестных моментов инерции необходимо оценить абсолютную и относительную погрешности измерений

Контрольные вопросы

1. Что называется моментом инерции тела относительно оси вращения?

В каких единицах измеряется момент инерции?

2. Может ли твердое тело иметь несколько моментов инерции?

3. Как связаны между собой момент силы и момент инерции тела?

4. Каким образом объясняется вращение фигуристов в пируэте?

Работа № 5-2 определение моментов инерции твердых тел с помощью маятника максвелла

Приборы и принадлежности: установка с маятником Максвелла и электронным блоком управления, набор сменных колец.

Описание установки и метода измерений

М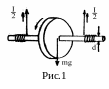 аятник Максвелла представляет собой массивный диск (маховик), насаженный на вал (рис. 1.). Диск подвешен на двух тонких нерастяжимых нитях, наматываемых на вал, а на этот диск надеваются толстостенные металлические кольца. При раскручивании нитей маятник опускается под действием силы тяжести с постоянным ускорением a, совершая одновременно вращательное и поступательное движения.

Как известно, закон сохранения механической энергии для тела массы m, одновременно вращающегося с угловой скоростью  и движущегося поступательно со скоростью , вид: , (1)

где П=mgh – потенциальная энергия тела массы m, поднятого на высоту h в поле силы тяжести; – кинетическая энергия вращающегося тела, где J – момент инерции этого тела; – кинетическая энергия тела, движущегося поступательно.

Обозначая натяжение каждой нити через Т/2, можно записать уравнения основного закона динамики для этих двух движений:

и , (2)

где m – масса маятника, g – ускорение свободного падения,  – угловое ускорение маятника, d – диаметр вала. Выражение представляет собой момент силы относительно вала.

Из кинематики вращательного движения известно, что угловое ускорение  связано с линейным ускорением a соотношением a=r (для нашего случая - радиус вала). Очевидно, что при раскручивании нитей маятник будет опускаться с некоторой высоты h по закону кинематики равноускоренного движения (3)

Исключая из системы (2) T, учитывая связь между величинами a и , а также уравнение (3), получим формулу для определения момента маятника

,где t – время падения маятника с высоты h. Поскольку >>1, то (4)

Таким образом, для нахождения момента инерции маятника нужно измерить время его падения t с определенной высоты h.

Схема экспериментальной установки изображена на рис. 2.

Подвес маятника смонтирован на вертикальной стойке 1, на которой закреплены два кронштейна – верхний 2 и нижний 3 с фотоэлектрическими датчиками. В верхнем положении маятник удерживается электромагнитом 4. Указатель на нижнем кронштейне позволяет измерить высоту, с которой падает маятник, по миллиметровой шкале на стойке прибора. Время падения маятника измеряется электронным секундомером, находящимся в блоке управления 5. Измерения моментов инерции проводятся с тремя кольцами, надеваемыми на диск маятника.