Работа № 5-1 определение моментов инерции твердых тел при помощи крутильных колебаний

Приборы и принадлежности: крутильный маятник, набор тел.

Описание установки Общий вид крутильного маятника показан на рис. 1.Крутильный

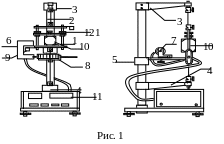маятник состоит из рамки 1, подвешенной с помощью стальной проволоки 2 к кронштейнам 3 и 4. На кронштейне 5 закреплена стальная плита, которая служит основанием фотоэлектрическому датчику 7 и угловой шкале 8. Электромагнит 7 может изменять положение на плите, а его положение относительно фотоэлектрического датчика указывает по угловой шкале стрелка 9, притягиваемая к электромагниту. Фотоэлектрический датчик и электромагнит соединены электронным секундомером 11.

Конструкция рамки позволяет закреплять исследуемые тела 10, значительно отличающиеся друг от друга по внешним размерам. Тела крепятся при помощи подвижной балки 12, которая перемещается по направляющим между неподвижными балками. Подвижная балка закрепляется путем затягивания гаек на зажимных втулках.

Описание метода определения моментов инерции твердых тел.

При отклонении рамки от положения равновесия возникает момент сил упругости (кручения) проволоки, пропорциональной по закону Гука углу закручивания  и направленный в противоположную сторону:

M= k, (1)

где k – коэффициент упругости проволоки. Тормозящим моментом сил трения, который будет в нашем случае мал по сравнению с моментом упругости можно пренебречь.

Таким образом, основной закон динамики для возникших крутильных колебаний M=J с учетом формулы углового ускорения запишется следующим образом:

или , (2)

где - угловое ускорение, а J – момент инерции рамки.

Уравнение (2) представляет собой дифференциальное уравнение гармонических колебаний. Решение его, как известно, является функция

, (3)

где ₀ – амплитуда,  - собственная циклическая частота,  - начальная фаза колебаний. Частота  может быть найдена подстановкой решения (3) в уравнение (2):: . (4)

Тогда период колебаний т будет равен: . (5)

Таким образом, нахождение моментов инерции тел можно свести к определению периода крутильных колебаний при известном коэффициенте упругости проволоки k.

Обозначим через J_k момент инерции исследуемого тела. Если коэффициент упругости k неизвестен, то найти J_k , определив период колебаний Т_эт, некоторого эталонного тела, имеющего известный момент инерции J_эт. В качестве эталонного тела можно взять любое тело, имеющее правильные геометрические размеры, момент инерции которого легко рассчитывается по известным формулам. (см. рис 5, стр. 6).

Итак, обозначим через J₀ момент инерции ненагруженной рамки. Тогда период ее колебаний будет равен , (6)

а период колебаний рамки с эталонным телом . (7)

Очевидно, что период колебания рамки с исследуемым телом

. (8)

Исключая из (6-8) коэффициент k, получим формулу для определения момента инерции исследуемого тела:

. (9)