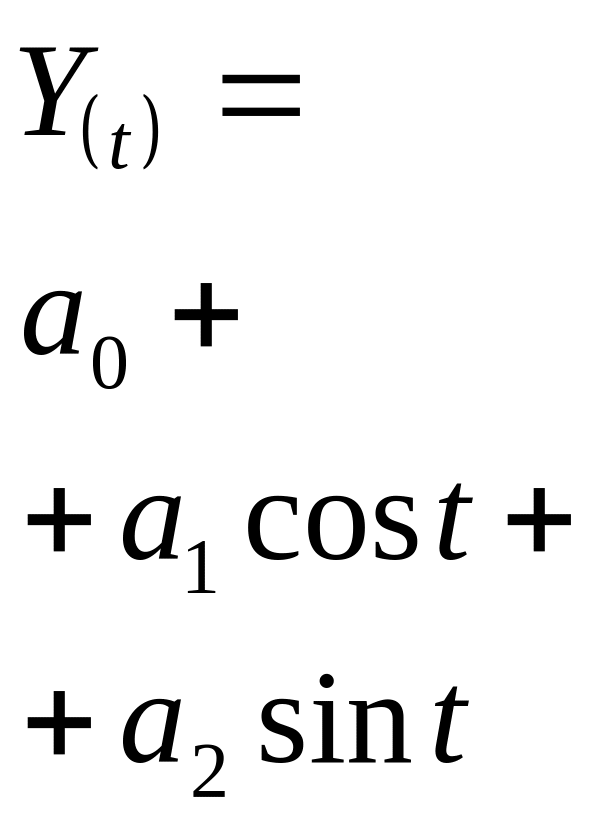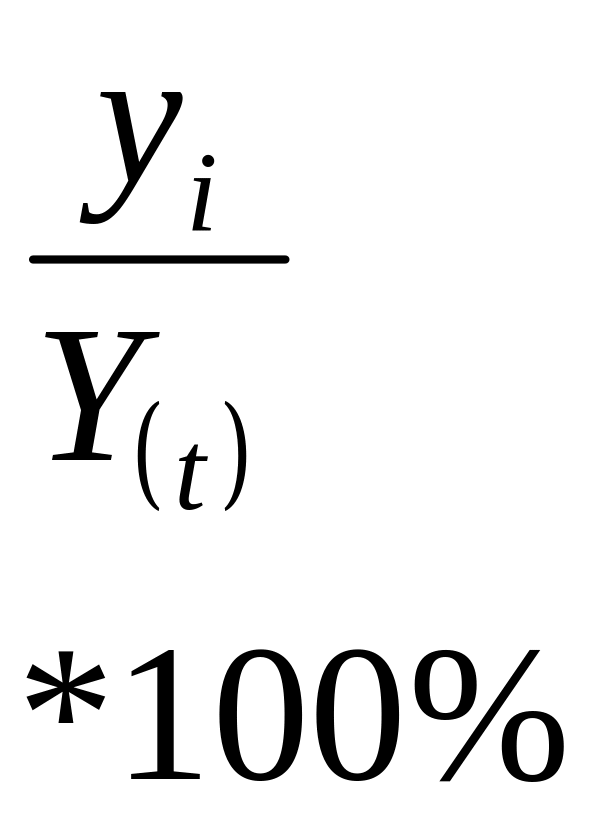- •Висновок
- •Розрахункова робота № 2 аналіз рядів розподілу
- •Висновки
- •Розрахункова робрта № 3 дисперсійний аналіз
- •Висновок
- •Розрахункова робота № 4 кореляційно_регресивний аналіз
- •Висновки
- •Розрахункова робота № 5 вимірювання сезонних коливань
- •Висновок
- •Перелік рекомендованих літературних джерел Основна література
- •Додаткова література
Висновки
Залежність між ціною і попитом описує однофакторна кореляційна модель Y(х) = 1070,23 – 10,0962 х. При зростанні ціни на 1 грн. обсяг попиту знижується на 10,0962 тис. т. При зростанні ціни на 1 % обсяг попиту знижується на 29,2 % і навпаки. Попит на продукцію є дуже еластичним. Варіація попиту на 99,64 % обумовлена впливом ціни. Існування дуже високого кореляційного зв’язку між ціною і попитом підтверджується. Побудована нами кореляційна модель є адекватною і може використовуватись для прогнозування обсягу попиту залежно від рівня цін. Якщо середня ціна знизиться до 100 грн., то з ймовірністю 0,95 слід очікувати, що попит на продукцію складатиме не більше 62,79 тис. т і не менше 58,43 тис. т.
Розрахункова робота № 5 вимірювання сезонних коливань
Завдання: Описати сезонну хвилю з урахуванням тенденції розвитку.
Таблиця 5.1 – Обсяг збуту продукції
Квартал |
Обсяг збуту, тис. грн. |
||
1-й рік |
2-й рік |
3-й рік |
|
І |
105 |
105 |
106 |
ІІ |
112 |
112 |
114 |
ІІІ |
106 |
106 |
109 |
ІV |
93 |
93 |
98 |
Разом |
416 |
416 |
427 |
Виявимо характер загальної тенденції ряду внутрішньорічної динаміки шляхом укрупнення квартальних періодів в річні рівні і визначення ланцюгових і базисних темпів зростання за такою схемою:
Таблиця 5.2 – Темпи росту обсягу збуту
Рік |
Річні рівні |
Темпи зростання, % |
|
Ланцюгові |
Базисні |
||
1 |
416 |
— |
100,00 |
2 |
416 |
100,00 |
100,00 |
3 |
427 |
102,60 |
102,60 |
Спостерігається нечітка тенденція до зростання.
Визначимо індекси сезонності за методом сталої середньої:
![]() ,
,
де — осереднені емпіричні рівні однойменних періодів;
— загальна, або стала середня рівня ряду.
Таблиця 5.3 – Розрахунок індексів сезонності методом сталої середньої
Рік |
Квартал |
Разом |
|||
І |
ІІ |
ІІІ |
ІV |
||
1 |
105 |
112 |
106 |
93 |
416 |
2 |
105 |
112 |
106 |
93 |
416 |
3 |
106 |
114 |
109 |
98 |
427 |
Разом |
316 |
338 |
321 |
284 |
1259 |
Середньоквартальний рівень за періодами, |
105,3 |
112,7 |
107,0 |
94,7 |
104,9 |
Індекси сезонності, Ісез, % |
100,4 |
107,4 |
102,0 |
90,3 |
100,0 |
Середньоквартальні рівні:
![]()
![]()
![]()
![]()
Загальна або стала середня рівня ряду:
![]()
або
![]()
Визначаємо індекси сезонності методом сталої середньої:
![]()
![]()
![]()
![]()
Для динамічних рядів, які виявляють тенденцію, індекси сезонності визначають за методом змінної середньої (виключення тренду). Індекси сезонності знаходимо за формулою:
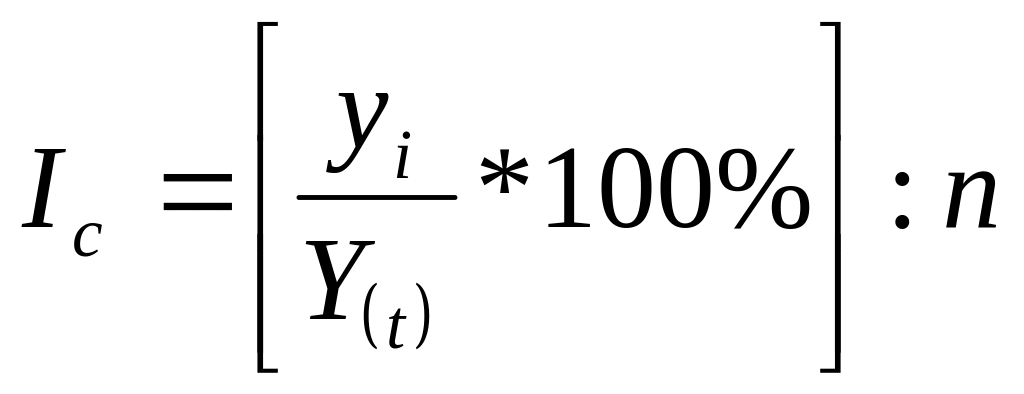 ,
,
де уі – емпіричні рівні ряду;
У(t) – теоретичні рівні ряду обчислені за рівнянням тренду;
n – число річних періодів.
Рівняння
тренду:
![]()
Для визначення а0 і а1 розв’язуємо систему нормальних рівнянь:
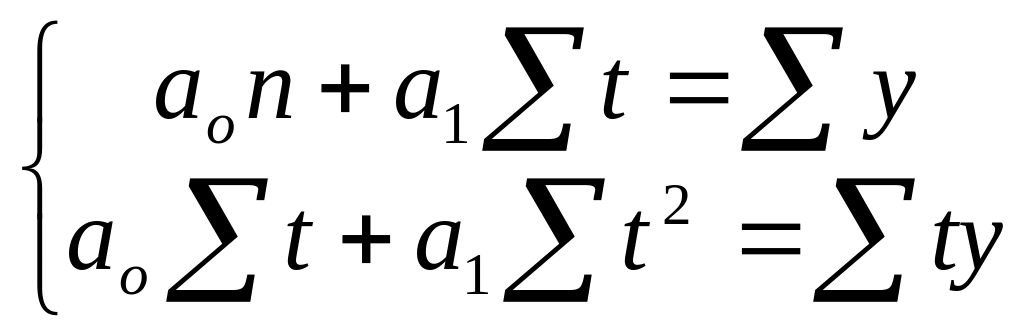
Відлік часу t перенесемо в середину ряду, тоді Σt = 0 і розв’язок системи значно спрощується:
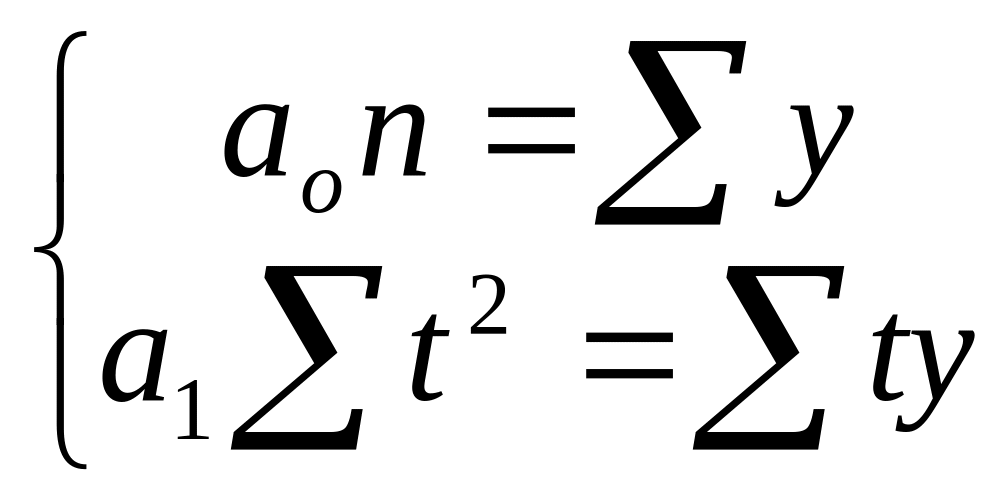
![]() ;
;
![]()
Трендові рівняння матиме вигляд: У(t) = - 0,0437 t + 104,9167. Знаходимо теоретичні значення У(t) і результати заносимо в таблицю 5.4.
Таблиця 5.4 – Розрахунок індексів сезонності методом змінної середньої
Рік |
Пері-од |
Об-сяг збуту тис. грн. у |
t |
t2 |
yt |
Yt |
|
|
|
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||
1 |
І |
105 |
- 11 |
121 |
-1155 |
105,40 |
100,00 |
- 0,40 |
0,16 |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||
|
ІІ |
112 |
- 9 |
81 |
-1008 |
105,31 |
106,00 |
6,69 |
44,76 |
||||
ІІІ |
106 |
- 7 |
49 |
-742 |
105,22 |
101,00 |
0,78 |
0,61 |
|||||
ІV |
93 |
- 5 |
25 |
-465 |
105,14 |
88,00 |
-12,14 |
147,38 |
|||||
2 |
І |
105 |
- 3 |
9 |
-315 |
105,05 |
100,00 |
-0,05 |
0,00 |
||||
Продовження таблиці 5.4
|
ІІ |
112 |
- 1 |
1 |
-112 |
104,96 |
107,00 |
7,04 |
49,56 |
ІІІ |
106 |
1 |
1 |
106 |
104,87 |
101,00 |
1,13 |
1,28 |
|
ІV |
93 |
3 |
9 |
279 |
104,79 |
89,00 |
-11,79 |
139,00 |
|
3 |
І |
106 |
5 |
25 |
530 |
104,70 |
101,00 |
1,3 |
1,69 |
ІІ |
114 |
7 |
49 |
798 |
104,61 |
109,00 |
9,39 |
88,17 |
|
ІІІ |
109 |
9 |
81 |
981 |
104,52 |
104,00 |
4,48 |
20,07 |
|
ІV |
98 |
11 |
121 |
1078 |
104,44 |
94,00 |
-6,44 |
41,47 |
|
Разом |
1259 |
0 |
572 |
-25 |
1259,01 |
Х |
Х |
Х |
|
Знаходимо індекси сезонності:
![]()
![]()
![]()
![]()
Будуємо лінійну діаграму:
Іс |
|
|
|
|
|
110 |
|
1 |
|
|
|
105 |
|
|
|
1 |
|
100 |
100,33 |
|
|
|
|
95 |
|
|
|
|
90,33 |
90 |
|
|
|
|
|
85 |
|
|
|
|
|
80 |
І кв. |
ІІ кв. |
ІІІ кв. |
ІV кв. |
|
Рис. 5.1. Сезонний характер збуту продукції
Узагальнені характеристики сезонних коливань
Амплітуда сезонних коливань:
![]()
Середнє лінійне відхилення сезонних коливань:
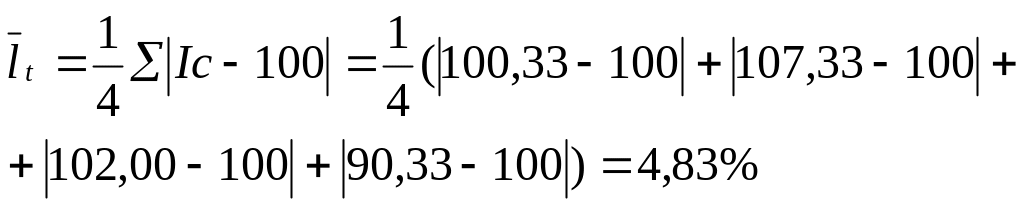
Середнє квадратичне
відхилення сезонних
коливань: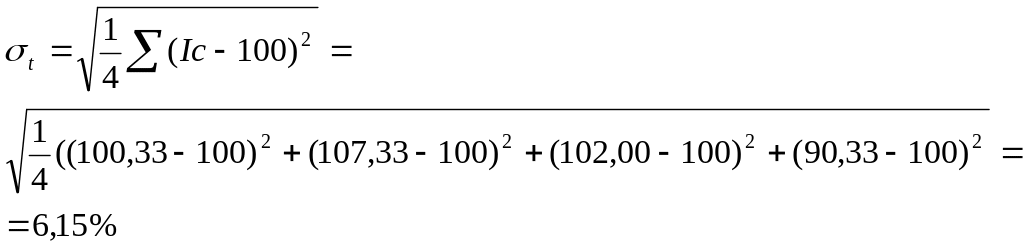 Визначимо
індекс сезонності на основі ковзної
(плинної) середньої:
Визначимо
індекс сезонності на основі ковзної
(плинної) середньої:
![]() , де
, де
уі – емпіричні рівні ряду;
![]() – згладжені
рівні ряду;
– згладжені
рівні ряду;
n – число річних періодів.
Таблиця 5.5- Розрахунок індексів сезонності методом плинної середньої
Рік |
Пері-од |
Вихідні рівні ряду, тис. грн. (уі) |
Середні з суми чотирьох рівнів ряду |
Згладжені
розрахункові рівні ряду
|
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
І |
105 |
|
|
|
ІІ |
112 |
104,00 |
|
|
|
ІІІ |
106 |
104,00 |
104,000 |
101,9 |
|
ІV |
93 |
104,00 |
104,000 |
89,4 |
|
2 |
І |
105 |
104,00 |
104,000 |
101,0 |
ІІ |
112 |
104,00 |
104,000 |
107,7 |
|
ІІІ |
106 |
104,25 |
104,125 |
101,8 |
|
ІV |
93 |
104,75 |
104,500 |
89,0 |
|
3 |
І |
106 |
105,50 |
105,125 |
100,8 |
ІІ |
114 |
106,75 |
106,125 |
107,4 |
|
ІІІ |
109 |
|
|
|
|
ІV |
98 |
|
|
|
Виконаємо згладжування ряду динаміки за допомогою ковзної середньої. При цьому застосуємо чотиричленні ковзні середні. Вони розраховуються з чотирьох рівнів ряду, використовуючи при обчисленні кожної нової середньої перший рівень і приєднуючи наступний рівень ряду:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Кожна з обчислених чотиричленних середніх належить до відповідних проміжків між двома суміжними кварталами. Так, перша середня належить до проміжку між ІІ і ІІІ кварталами 1-го року, друга середня – до проміжку між ІІІ і ІV кварталами 1-го року і т.д.
А тому, щоб обчислити значення згладжених рівнів, треба провести центрування розрахункових середніх. Так, для визначення згладженого середнього рівня ряду ІІІ кварталу 1-го року зробимо центрування першої і другої середніх і т.д. Результати розрахунків подаємо в таблиці 5.5.
1–й рік |
|
|
|
2–й рік |
|
|
|
|
|
|
|
3–й рік |
|
|
Обчислюємо
відношення
![]()
1–й рік |
ІІІ
кв.
|
IV
кв.
|
|
2–й рік |
І
кв.
|
ІІ
кв.
|
|
ІІІ
кв.
|
|
IV
кв.
|
|
3–й рік |
І
кв.
|
ІІ
кв.
|
Усереднимо обчислені величини за однойменними періодами – кварталами року в результаті чого одержимо індекси сезонності, які характеризують сезонну хвилю обсягу збуту (у процентах до середньоквартальної реалізації, узятої за 100%).
![]()
![]()
![]()
![]()
Визначимо
індекси сезонності методом Персонса.
![]() , де
, де
– базисні індекси за і-й квартал;
![]() – середньорічний
індекс.
– середньорічний
індекс.
Таблиця 5.6 – Розрахунок індексів сезонності методом Персонса
Квартал |
Обсяг збуту, тис. грн. |
Ланцюгові індекси |
Середні ланцюгові індекси |
Базисні індек-си уі |
Індекси сезон-ності % |
||||
1-й рік |
2-й рік |
3-й рік |
1-й рік |
2-й рік |
3-й рік |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
І |
105 |
105 |
106 |
- |
1,129 |
1,140 |
1,135 |
1,000 |
100,4 |
ІІ |
112 |
112 |
114 |
1,067 |
1,067 |
1,076 |
1,070 |
1,070 |
107,4 |
Продовження таблиці 5.6
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
ІІІ |
106 |
106 |
109 |
0,946 |
0,946 |
0,956 |
0,949 |
1,015 |
101,9 |
ІV |
93 |
93 |
98 |
0,877 |
0,877 |
0,899 |
0,884 |
0,898 |
90,2 |
Разом |
416 |
416 |
427 |
2,89 |
4,019 |
4,071 |
- |
3,983 |
400,0 |
В середньому |
- |
- |
- |
0,963 |
1,005 |
1,018 |
- |
0,996 |
100,0 |
Визначимо ланцюгові індекси:
1-й рік |
ІІ кв. |
|
|
ІІІ кв. |
|
|
IV кв. |
|
2-й рік |
І кв. |
|
|
ІІ кв. |
|
|
ІІІ кв. |
|
|
IV кв. |
|
3-й рік |
І кв. |
|
|
ІІ кв. |
|
|
ІІІ кв. |
|
|
IV кв. |
|
Визначимо середні ланцюгові індекси:
І кв.
![]()
ІІ кв.
![]()
ІІІ кв.
![]()
IV
кв.
![]()
Визначимо базисні індекси:
І кв.
Приймемо середню першого кварталу за
100%.
![]()
ІІ кв.
Залишимо середню другого кварталу без
зміни.
![]()
ІІІ кв.
![]()
IV кв.
![]()
Визначимо середньорічний індекс:
![]()
Визначимо індекси сезонності:
![]()
![]()
![]()
![]()
Моделювання
сезонних коливань проведемо за допомогою
ряду Фур’є, аналітичний вираз якого
має вигляд
![]() ,
де
,
де
k - ступінь точності гармоніки тригонометричного многочлена;
t - час, виражений в радіанах або градусах.
Для першої гармоніки (k= 1) рівняння Фур’є матиме вигляд:
![]()
Параметри рівняння розраховуємо за формулами:
![]() ;
;
![]() ;
;
![]()
Таблиця 5.7 – Розрахунок індексів сезонності за допомогою рівнянь ряду Фур’є
Рік |
Квар-тал |
t, раді-ан |
Обсяг збуту, тис. грн. (у) |
cos t |
sin t |
y cos t |
y sin t |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1-й |
І |
0 |
105 |
1,000 |
0,000 |
105,00 |
0,00 |
105,81 |
99,2 |
ІІ |
π/6 |
112 |
0,866 |
0,500 |
96,99 |
56,00 |
105,02 |
106,7 |
|
ІІІ |
π/3 |
106 |
0,500 |
0,866 |
53,00 |
91,80 |
104,22 |
101,7 |
|
IV |
π/2 |
93 |
0,000 |
1,000 |
0,00 |
93,00 |
103,59 |
89,8 |
|
2-й |
І |
2π/3 |
105 |
-0,500 |
0,866 |
-52,50 |
90,93 |
103,32 |
101,6 |
ІІ |
5π/6 |
112 |
-0,866 |
0,500 |
-96,99 |
56,00 |
103,48 |
108,2 |
|
ІІІ |
π |
106 |
-1,000 |
0,000 |
-106,00 |
0,00 |
104,03 |
101,9 |
|
IV |
7π/6 |
93 |
-0,866 |
-0,500 |
-80,54 |
-46,50 |
104,82 |
88,7 |
|
3-й |
І |
4π/3 |
106 |
-0,500 |
-0,866 |
-53,00 |
-91,80 |
105,62 |
100,4 |
ІІ |
3π/2 |
114 |
0,000 |
-1,000 |
0,00 |
-114,00 |
106,25 |
107,3 |
|
ІІІ |
5π/3 |
109 |
0,500 |
-0,866 |
54,50 |
-94,39 |
106,52 |
102,3 |
|
IV |
11π/6 |
98 |
0,866 |
-0,500 |
84,87 |
-49,00 |
106,36 |
92,1 |
|
Разом |
Х |
1259 |
Х |
Х |
5,33 |
-7,96 |
1259,04 |
Х |
|
![]() ;
;
![]() ;
;![]()
Звідси рівняння Фур’є матиме вигляд:
У(t) = 104,92 + 0,89 cos t – 1,33 sin t
Теоретичні значення обсягу збуту в розрізі кварталів року
У(t)1 = 104,92 + 0,89*1 – 1,33*0 = 105,81
У(t)2 = 104,92 + 0,89*0,866 – 1,33*0,5 = 105,02
У(t)3 = 104,92 + 0,89*0,5 – 1,33*0,866 = 104,22
У(t)4 = 104,92 + 0,89*0 – 1,33*1 = 103,59
У(t)5 = 104,92 + 0,89*(-0,5) – 1,33*0,866 = 103,32
У(t)6 = 104,92 + 0,89*(-0,866) – 1,33*0,5 = 103,48
У(t)7 = 104,92 + 0,89*(-1) – 1,33*0 = 104,03
У(t)8 = 104,92 + 0,89*(-0,866) – 1,33*(-0,5) = 104,82
У(t)9 = 104,92 + 0,89*(-0,5) – 1,33*(-0,866) = 105,62
У(t)10 = 104,92 + 0,89*0 – 1,33*(-1) = 106,25
У(t)11 = 104,92 + 0,89*0,5 – 1,33*(-0,866) = 106,52
У(t)12 = 104,92 + 0,89*0,866 – 1,33*(-0,5) = 106,36
Результати обчислень заносимо в таблицю 5.7. Як показують дані таблиці 5.7, уже перша гармоніка ряду Фур’є (k = 1) досить добре апроксимує емпіричний ряд динаміки.
Визначаємо
сезонну хвилю обсягу збуту (відношення
емпіричних і теоретичних рівнів)за
формулою
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Результати обчислень занесемо в таблицю 5.7.
Індекси
сезонності представляють собою відношення
середніх з фактичних рівнів однойменних
кварталів за період, що розглядається,
до середніх з вирівняних даних за ті ж
самі квартали, або
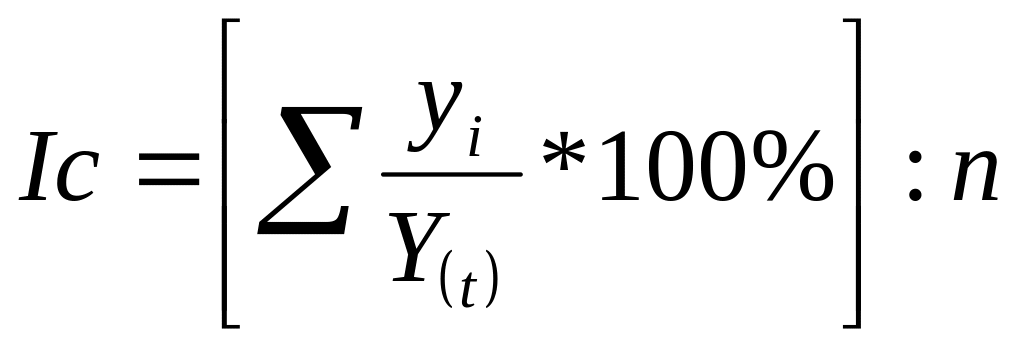 .
.
![]()
![]()
![]()
![]()
Якщо розраховані нами індекси сезонності достатньо надійні і точні, а це так, оскільки їх значення виявилися однаковими при будь-яких способах обчислення, то це дозволяє нам використати їх для екстраполяції.
Для розрахунку показників обсягу збуту продукції на перспективу використаємо модель прогнозу наступного виду:
У(t) = Ick*Y(t) + εt , де
У(t) – обсяг збуту в момент часу t;
Ick – індекс сезонності k-го кварталу;
Y(t) – оцінка обсягу попиту в момент часу t;
εt – випадковий компонент.
Показники
прогнозу відрізняються від фактичних
на величину:
![]() ,
де
,
де
t – число, яке гарантує з певною ймовірністю межі прогнозу (для ймовірності 0,9545 t = 2);
σεt – середнє квадратичне відхилення випадкового компонента;
n – кількість річних періодів.
![]()
Межі прогнозу
![]()
Для визначення прогнозованих обсягів збуту на наступний 4-й рік використаємо дані таблиці 5.4 та значення індексів сезонності, обчислені методом змінної середньої (виключення тренду на основі аналітичного вирівнювання за рівнянням прямої). Трендове рівняння має вигляд: Y(t) = 104,9167 - 0,0437 t. Розрахунок величини виконаємо при допомозі таблиці 5.8.
Таблиця 5.8 – Розрахунок величини
Квартал |
Індекси сезонності, % |
|
|
|
1 |
2 |
3 |
4 |
5 |
І |
100,33 |
1,85 |
0,96 |
1,11 |
ІІ |
107,33 |
182,49 |
9,55 |
11,08 |
ІІІ |
102,00 |
21,96 |
3,31 |
3,84 |
IV |
90,33 |
327,85 |
12,80 |
14,85 |
І квартал
![]()
![]()
![]() і т.д.
і т.д.
Прогноз на 4-й рік:
І квартал у1 = 1,0033*[104,9167 – 0,0437 (13)] = 104,69 тис. т.
Межі прогнозу:
104,69 – 1,11 ≤ у1 ≤ 104,69 + 1,11
103,58 ≤ у1 ≤ 105,80
Результати обчислення прогнозованих обсягів збуту представимо в таблиці 5.9.
Таблиця 5.9 – Прогноз обсягу збуту продукції на 4-й рік в тис. т
Квартал |
Прогноз |
Нижня межа |
Верхня межа |
1 |
2 |
3 |
4 |
І |
104,69 |
103,58 |
105,80 |
ІІ |
111,90 |
100,82 |
122,98 |
ІІІ |
106,26 |
102,42 |
110,10 |
IV |
94,021 |
89,24 |
118,94 |

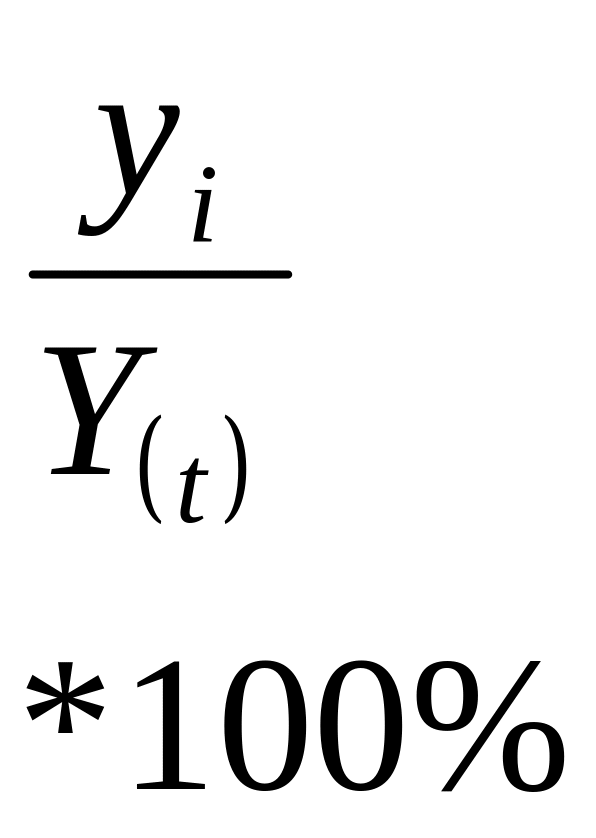
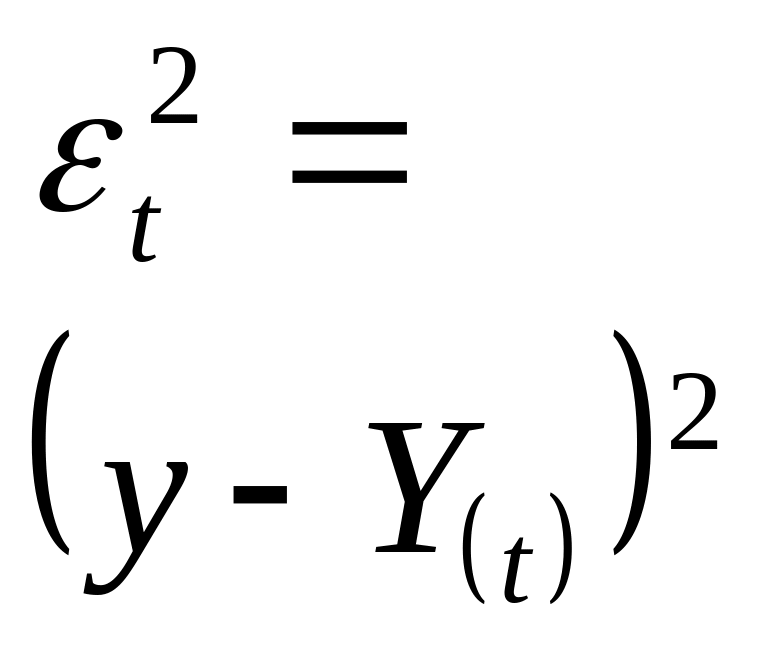
 07,33
07,33
 02,00
02,00