Висновок

Варіація обсягу попиту на 95,42 % зумовлена впливом ціни за одиницю продукції. Кореляційний зв’язок між ціною і попитом високий і достовірний. Виявивши тісний зв’язок в окремих точках емпіричної лінії регресїї можна оцінити тісноту зв’язку між ціною і попитом безпосередньо впродовж усієї лінії регресії.

Розрахункова робота № 4 кореляційно_регресивний аналіз

Завдання: Провести кореляційно-регресійний аналіз. Для цього визначити функцію, яка описує залежність між факторною та результативною ознаками, обчислити параметри рівняння регресії та пояснити їх зміст, оцінити тісноту зв’язку та перевірити зв’язок на істотність.

Вибір форми зв’язку між факторною та результативною ознаками. Будуємо кореляційне поле, на яке наносимо значення х і у для кожної одиниці статистичної сукупності.

у
60
50
40
30
20		У = - 10,096 х +1070,2
10
0	100	101	102	103	104	105	106	х

Рисунок 4.1 – Кореляційне поле та теоретична лінія регресії

За скупченням точок на кореляційному полі можна зробити висновок, що рівняння прямої найбільш точно відображає зв’язок між факторною і результативною ознаками.

Обчислення параметрів рівняння регресії.

Рівняння регресії матиме вигляд:

Розрахунки його параметрів представимо в таблиці 4.1.

Таблиця 4.1 – Розрахунок параметрів рівняння регресії

№ з/п	х	у	х2	ху	ух
1	2	3	4	5	6
1	100,3	58	10060,09	5817,4	57,58
2	102,7	36	10547,29	3697,2	33,35
3	103,5	25	10712,25	2587,5	25,27
4	100,0	60	10000,00	6000,0	60,61
5	102,5	35	10506,25	3587,5	35,37
6	103,8	22	10774,44	2283,6	22,24
7	101,0	50	10201,00	5050,0	50,51
8	104,0	20	10816,00	2080,0	20,23
9	101,5	45	10302,25	4567,5	45,47
10	103,0	30	10609,00	3090,0	30,32
11	102,2	38	10444,84	3883,6	38,40
12	101,8	44	10363,24	4479,2	42,44
13	102,0	40	10404,00	4080,0	40,42
14	104,5	15	10920,25	1567,5	15,18
15	102,1	39	10424,41	3981,9	39,41
16	105,0	10	11025,00	1050,0	10,13
Разом	1639,9	567	168110,31	57802,9	566,92

Параметри рівняння знаходимо за методом найменших квадратів із системи нормальних рівнянь.

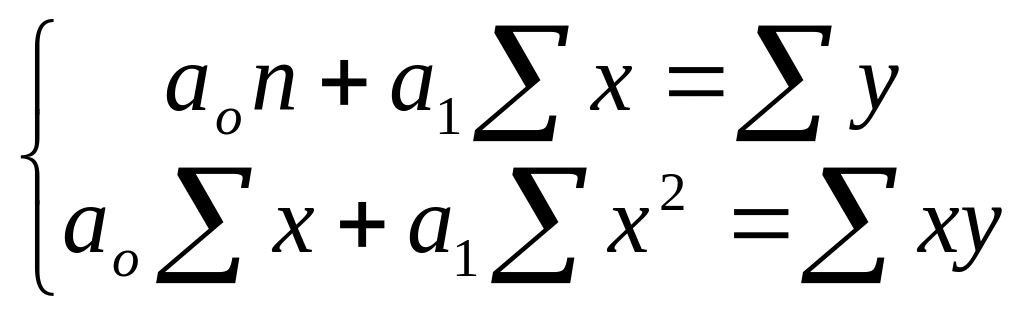
Δ =		16		1639,9		= 492,95
		1639,9		168110,31
Δ0 =	567		1639,9		= 527570,06
	57802,9		168110,31

Δ1 =	16	567	= - 4976,9
	1639,9	57802,9

Рівняння регресії має вигляд Y = -10,0962 х + 1070,230

Для кожного із значень факторної ознаки обчислюємо значення Y(х) і результати заносимо в таблицю 4.1. Теоретичні рівні Y(х) наносимо на кореляційне поле і з’єднуємо прямою лінією (рис.4.1). Отримуємо теоретичну лінію регресії.

коефіцієнт еластичності попиту за цінами:

_х=

Вимірювання тісноти зв’язку

Обчислюємо теоретичне кореляційне відношення, індекс кореляції, коефіцієнт детермінації:

 = ;

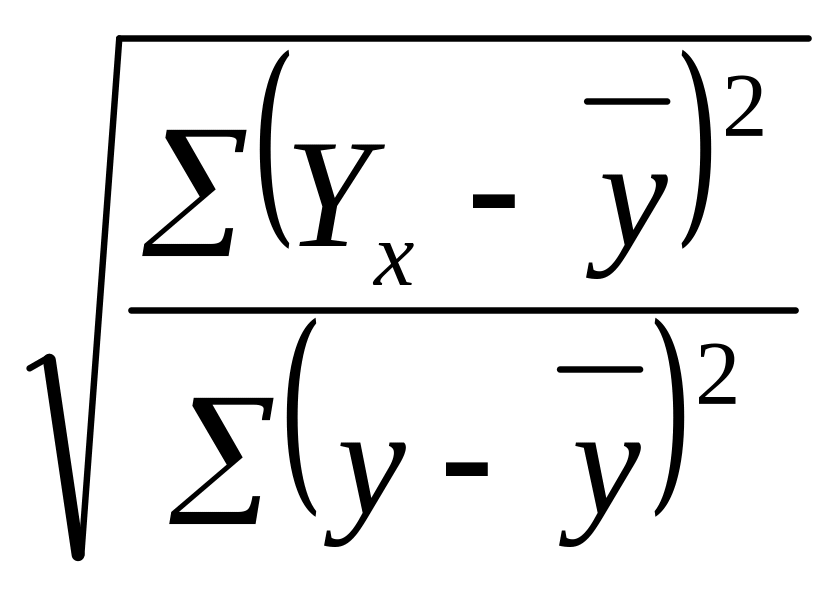Розрахунки представимо в таблиці 4.2.

Таблиця 4.2 – Розрахунок теоретичного кореляційного відношення, індексу кореляції

№ з/п	x
1	100,3	58	22,563	509,066	57,58	22,144	490,341	0,42	0,1764
2	102,7	36	0,563	0,316	33,35	-2,087	4,357	2,65	7,0225
3	103,5	25	-10,438	108,941	25,27	-10,164	103,311	-0,27	0,0729
4	100,0	60	24,563	603,316	60,61	25,173	633,655	-0,61	0,3721
5	102,5	35	-0,438	0,191	35,37	-0,068	0,005	-0,37	0,1369
6	103,8	22	-13,438	180,566	22,24	-13,193	174,057	-0,24	0,0576
7	101,0	50	14,563	212,066	50,51	15,076	227,295	-0,51	0,2601
8	104,0	20	-15,438	238,316	20,23	-15,212	231,414	-0,23	0,0529
9	101,5	45	9,563	91,441	45,47	10,028	100,565	-0,47	0,2209
10	103,0	30	-5,438	29,566	30,32	-5,116	26,174	-0,32	0,1024
11	102,2	38	2,563	6,566	28,40	2,961	8,767	-0,40	0,1600
12	101,8	44	8,563	73,316	42,44	6,999	48,991	1,56	2,4336
13	102,0	40	4,563	20,816	40,42	4,980	24,801	-0,42	0,1764
14	104,5	15	-20,438	417,691	15,18	-20,260	410,484	-0,18	0,0324
15	102,1	39	3,563	12,691	39,41	3,970	15,765	-0,41	0,1681
16	105,0	10	-25,438	647,066	10,13	-25,308	640,520	-0,13	0,0169
Разом	1639,9	567	Х	3151,931	566,92	Х	3140,502	Х	11,4621

; R =

Коефіцієнт детермінації η² = R² = 0,9964.

Так як рівняння регресії має вигляд прямої, то обчислюємо лінійний коефіцієнт кореляції. Розрахунки проводимо в таблиці 4.3.

Таблиця 4.3 – Розрахунок лінійного коефіцієнта кореляції

№ з/п			Розрахункові величини
							ху
1	100,3	58	-2,194	4,813	22,563	509,066	5817,4
2	102,7	36	0,206	0,043	0,563	0,316	3697,2
3	103,5	25	1,006	1,013	-10,438	108,941	2587,5
4	100,0	60	-2,494	6,219	24,563	603,316	6000,0
5	102,5	35	0,006	0,000	-0,438	0,191	3587,5
6	103,8	22	1,306	1,706	-13,438	180,566	2283,6
7	101,0	50	-1,494	2,231	14,563	212,066	5050,0
8	104,0	20	1,506	2,269	-15,438	238,316	2080,0
9	101,5	45	-0,994	0,988	9,563	91,441	4567,5
10	103,0	30	0,506	0,256	-5,438	29,566	3090,0
11	102,2	38	-0,294	0,086	2,563	6,566	3883,6
12	101,8	44	-0,694	0,481	8,563	73,316	4479,2
13	102,0	40	-0,494	0,244	4,563	20,816	4080,0
14	104,5	15	2,006	4,025	-20,438	417,691	1567,5
15	102,1	39	-0,394	0,155	3,563	12,691	3981,9
16	105,0	10	2,506	6,281	-25,438	647,066	1050,0
Разом	1639,9	567	Х	30,809	Х	3151,931	57802,9

Обчислимо лінійний коефіцієнт кореляції:

r =

Середні значення

=

Середні квадратичні відхилення

r = =

|r|= 0,9911; |η- |r|| = |0,9982 – 0,9911| = 0,0071 < 0,1, що підтверджує гіпотезу про лінійну форму зв’язку.

Оцінка достовірності лінійного коефіцієнта кореляції шляхом зіставлення його числового значення із стандартною похибкою σ_r .

; для n < 50

= > , лінійний коефіцієнт кореляції значущий, а зв’язок реальний.

Перевіримо кореляційну модель на адекватність за допомогою F-критерію Фішера:

_,

де k₂ – ступінь вільності для залишкової дисперсії;

k₁ – ступінь вільності для факторної дисперсії.

k₂ = n – m, де m – число параметрів рівняння регресії.

k₁ = m – 1, k₂ = 16 – 2 = 14, k₁ = 2 – 1 = 1,

_{= ,} F_0,95 (14; 1) = 4,6;

F > F_0,95 (14; 1)

Регресійна модель є адекватною і може використовуватись для прогнозування.

Припустимо, що середня ціна знизиться до 100 грн., тоді слід очікувати, то попит на продукцію складатиме Y_(x)0 = 1070,23 – 10,0962*100 = 60,61 тис. т. Знайдемо інтервал довіри для індивідуального значення залежної змінної за формулою:

Y_(x) ± ,

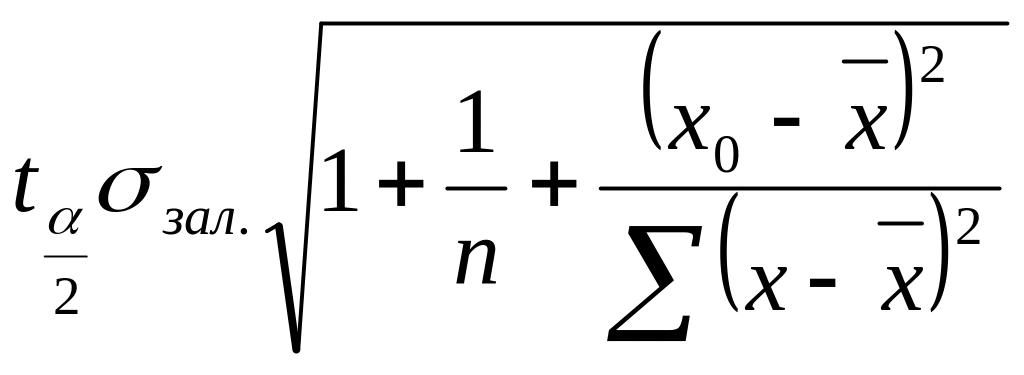- статистична характеристика (t –критерій Стьюдента) для рівня істотності α/2; для рівня значущості α/2 = 0,05 і числа ступенів вільності k = n – 2 = 16 – 2 = 14, критичне значення t_0.95 (14) = 2,145.

х₀ – задане значення незалежної змінної;

σ²_зал. – залишкова дисперсія.

Середню квадратичну похибку залишків обчислюють за формулою:

σ_зал. =

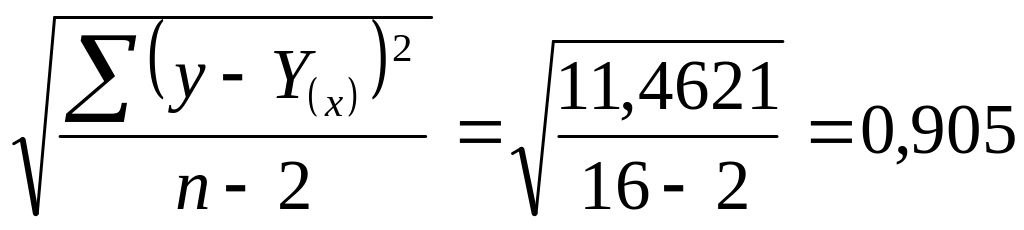
З імовірністю 0,95 можна стверджувати, що для х₀ =

100 грн. прогнозні значення обсягу попиту будуть знаходитися в межах:

60,61 ± 2,145*0,905

або

Перевіримо також значущість коефіцієнта регресії та визначимо його область зміни:

,

Оскільки розрахункове значення t – критерію Стьюдента значно перевищує критичне значення для ймовірності 0,95 і ступеня вільності 14 (t_0,95 (14) = 2,145), то коефіцієнт регресії визнаємо значущим. Знайдемо стандартну похибку коефіцієнта регресії:

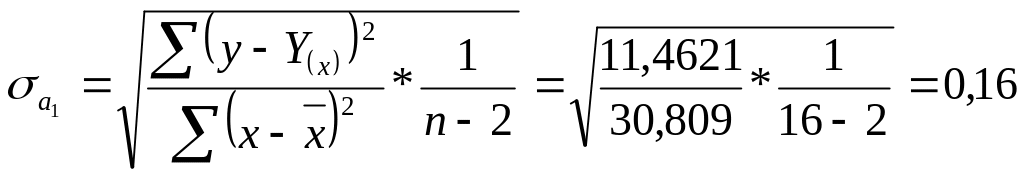
Довірчі межі коефіцієнта регресії:

або

-10,4362 ≤ а₁ ≤ -9,7562

З ймовірністю 0,95 можна вважати, що і коефіцієнт еластичності знаходиться в межах - 29,54 % ≤ е_х ≤ - 28,86 %.