
- •Висновок
- •Розрахункова робота № 2 аналіз рядів розподілу
- •Висновки
- •Розрахункова робрта № 3 дисперсійний аналіз
- •Висновок
- •Розрахункова робота № 4 кореляційно_регресивний аналіз
- •Висновки
- •Розрахункова робота № 5 вимірювання сезонних коливань
- •Висновок
- •Перелік рекомендованих літературних джерел Основна література
- •Додаткова література
Висновки
Встановлена така закономірність розподілу покупців за ціною. Середня ціна за одиницю продукції складає 102,38 грн. Половина покупців мають намір придбати продукцію за ціною до 102,40 грн., а решта – понад 102,40 грн. Найчастіше зустрічалися покупці, які мали намір придбати продукцію за ціною 102,50 грн.
Розмах варіації ціни складав 5 грн. Середнє лінійне відхилення від середньої ціни становило 1,033 грн., а середнє квадратичне відхилення – 1,262 грн. Сукупність покупців за ціною є однорідною, а ціна – типовою для досліджуваної групи покупців.
Розподіл покупців за ціною та обсягом попиту підлягає закону нормального розподілу. Розходження між теоретичними та емпіричними частотами випадкове. Слабка правостороння асиметрія виявилась неістотною, а ексцес для цього розподілу не властивий. Оскільки незалежна і залежна змінні тяжіють до нормального розподілу, це дає підстави провести дисперсійний та кореляційно-регресійний аналізи.
Розрахункова робрта № 3 дисперсійний аналіз
Завдання: Виконати дисперсійний аналіз. Для цього використати результати аналітичного групування за факторною ознакою в розрахунковій роботі № 1 та значення результативної ознаки по кожній одиниці статистичної сукупності, які містяться у вихідних даних.
Таблиця 3.1 – Розрахунок міжгрупової та внутрішньогрупової девіацій
Групи покуп-ців за ціною |
х |
у |
Суми варі-ант уі |
Час-тоти, fі |
Групові середні
|
|
|
Квадрат відхилень
|
Відхилення варіант від груп сер.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
100 – 101 |
100,0 |
60 |
168,0 |
3 |
56,000 |
20,562 |
422,796 |
1268,3880 |
16.000 |
100,3 |
58 |
4.000 |
|||||||
101,0 |
50 |
36.000 |
|||||||
101 – 102 |
101,5 |
45 |
129,0 |
3 |
43,000 |
7,562 |
57,184 |
171,5515 |
4,000 |
101,8 |
44 |
1,000 |
|||||||
102,0 |
40 |
9,000 |
|||||||
102 – 103 |
102,1 |
39 |
178,0 |
5 |
35,600 |
0,162 |
0,026 |
0,13122 |
11,560 |
102,2 |
38 |
5,760 |
|||||||
102,5 |
35 |
0,360 |
|||||||
102,7 |
36 |
0,160 |
|||||||
103,0 |
30 |
31,360 |
|||||||
103 – 104 |
103,5 |
25 |
67,0 |
3 |
22,333 |
-13,105 |
171,741 |
515,2231 |
7,113 |
103,8 |
22 |
0,111 |
|||||||
104,0 |
20 |
5,443 |
|||||||
104 – 105 |
104,5 |
15 |
25,0 |
2 |
12,500 |
-22,938 |
526,152 |
1052,304 |
6,250 |
105,0 |
10 |
6,250 |
|||||||
Разом |
1639,9 |
567 |
567,0 |
Х |
х |
Х |
Х |
3007,597 |
144,367 |
Обчислимо
загальну середню за формулою
![]() ,
а також міжгрупову
,
а також міжгрупову
![]() та внутрішньогрупову
та внутрішньогрупову
![]() девіації за формулами :
девіації за формулами :
![]() fi
;
fi
;
![]() 2
2
=
![]()
![]() ;
;
![]()
У відповідності з правилом додавання девіацій обчислюємо загальну девіацію за формулою:
![]()
Обчислюємо коефіцієнт детермінації за формулою:
![]()
Визначимо емпіричне кореляційне відношення за формулою:
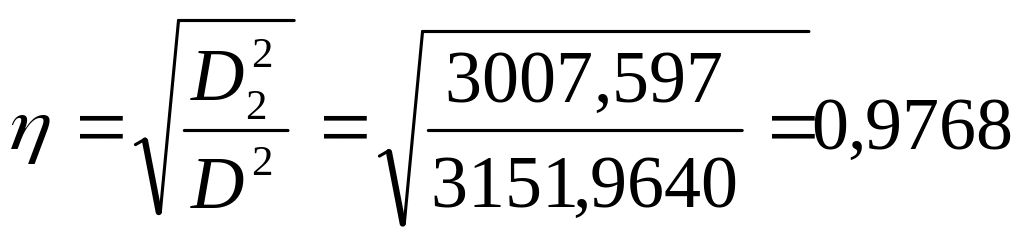
Перевіряємо
істотність кореляційного зв’язку при
допомозі F-
критерію Фішера, який обчислюємо за
формулою:
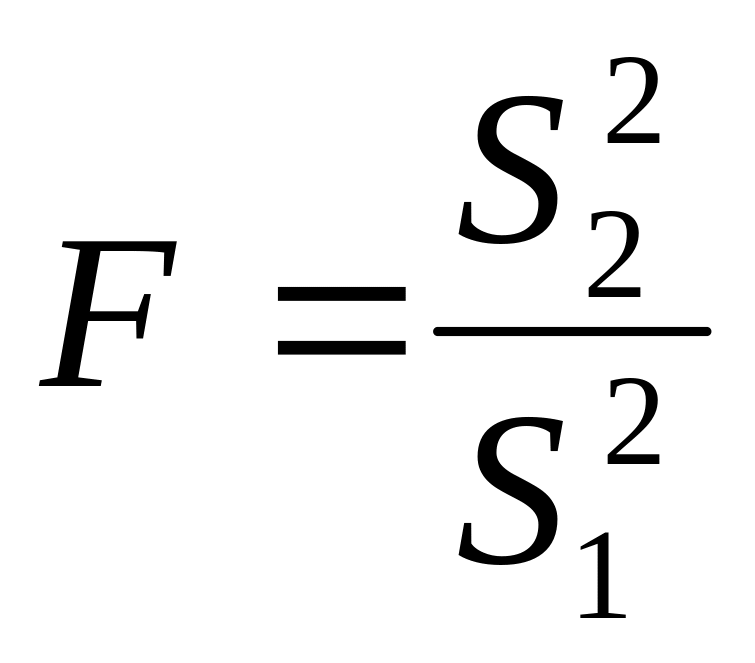 ,
при
,
при
![]() і
і
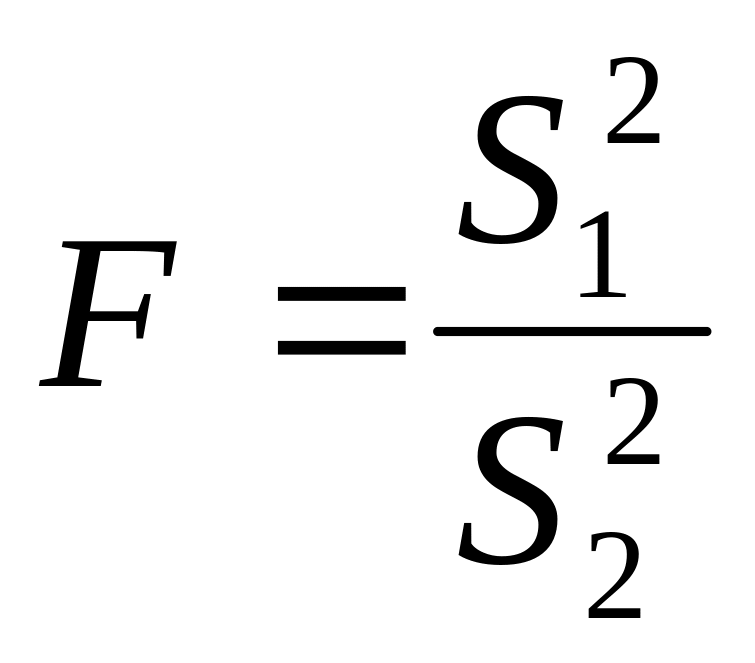 ,
при
,
при
![]() ,
де
,
де
![]() - оцінювальні дисперсії, які обчислюють
за формулами:
- оцінювальні дисперсії, які обчислюють
за формулами:
![]() ;
;
![]()
де n = 16 – чисельність одиниць сукупності; m = 5 – число груп, утворених за факторною ознакою.
![]() ;
;
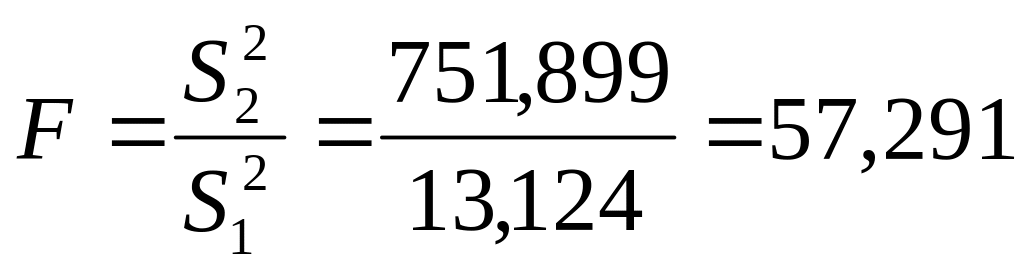
За ймовірностями 0,95 і 0,99 і за ступенями вільності k1 = m – 1 = 5 – 1 = 4; k2 = n – m = 16 – 5 = 11, знаходимо критичні значення F- критерію Фішера і порівнюємо їх з фактичними значеннями.
F0,95(k1 = 4; k2 = 11) = 3,357 < Fрозр. = 57,291
F0,99(k1
= 4; k2 =
11) = 5,668 < Fрозр.
= 57,291, що дозволяє з
ймовірністю 0,99 та 0,95 стверджувати про
істотність кореляційного зв’язку між
ціною та обсягом попиту. Загальна
оцінювальна дисперсія визначається за
формулами:
![]() або
або
![]() ;
;
![]()
Результати розрахунків заносимо в таблицю 3.2
Таблиця 3.2 – Одновимірний дисперсійний аналіз
Варіація |
Сума кв. відхилень D2 |
Число ступенів вільності |
Оцінювальні дисперсії
|
Відношення дисперсій F |
Табличні значення F–критерію з ймовірністю |
|
0,95 |
0,99 |
|||||
Систематична |
3007,597 |
4 |
751,899 |
57,291 |
3,357 |
5,668 |
Залишкова |
144,367 |
11 |
13,124 |
|||
Загальна |
3151,964 |
15 |
210,131 |
- |
- |
- |
Проведемо дисперсійний аналіз іншим способом.
Визначимо систематичну (міжгрупову) та залишкову (внутрішньогрупову) дисперсії, використавши згруповані дані, а загальну дисперсію способом різниці квадратів, використавши незгруповані дані. Розрахунки представимо в таблиці 3.3
Таблиця 3.3 – Розрахунок загальної дисперсії способом різниці квадратів
№ покупця |
y |
y2 |
1 |
58 |
3364 |
2 |
36 |
1296 |
3 |
25 |
625 |
4 |
60 |
3600 |
5 |
35 |
1225 |
6 |
22 |
484 |
7 |
50 |
2500 |
8 |
20 |
400 |
9 |
45 |
2025 |
10 |
30 |
900 |
11 |
38 |
1444 |
12 |
44 |
1936 |
13 |
40 |
1600 |
14 |
15 |
225 |
15 |
39 |
1521 |
16 |
10 |
100 |
Разом |
567 |
23245 |
![]()
Загальна девіація:
![]()
Загальна оцінювальна дисперсія:
![]()
Систематичну варіацію результативної ознаки визначаємо за допомогою таблиці 3.4.
Таблиця 3.4 – Розрахунок міжгрупової девіації з використанням згрупованих даних
Групи покупців за ціною |
fi |
Σyi |
|
- |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
100 – 101 |
3 |
168 |
56,000 |
20,562 |
422,796 |
1268,388 |
101 – 102 |
3 |
129 |
43,000 |
7,562 |
57,184 |
171,552 |
102 – 103 |
5 |
178 |
35,600 |
0,162 |
0,026 |
0,131 |
103 – 104 |
3 |
67 |
22,333 |
-13,105 |
171,741 |
515,223 |
104 – 105 |
2 |
25 |
12,500 |
-22,938 |
526,152 |
1052,304 |
Разом |
16 |
567 |
35,44 |
Х |
Х |
3007,598 |
Міжгрупова
девіація:
![]()
Міжгрупрова оцінювальна дисперсія:
![]()
За правилом складання девіацій:
![]()
Внутрішньо групова оцінювальна дисперсія:
![]()
F – критерій Фішера
