
- •Сигнали та їх спектри.
- •8.1. Динамічне представлення сигналів.
- •8.1.1.Імпульсні та перехідні характеристики лінійних систем.
- •8.2.Геометричні методи в теорії сигналів.
- •8.2.1.Коефіцієнт кореляції. Кореляційні функції.
- •8.2.2.Взаємно кореляційні функції. Когерентність.
- •8.3.Спектральний аналіз.
- •8.3.1.Тригонометричний ряд Фур’є.
- •8.3.3.Основні властивості перетворення Фур’є.
- •8.3.4.Спектральний метод.
- •8.3.5. Зв’язок між характеристиками лінійного кола.
- •8.3.6.Енергетичні характеристики сигналу у частотній області.
- •8.4.Спектри модульованих сигналів.
- •8.4.2.Кутова модуляція.
8.2.Геометричні методи в теорії сигналів.
8.2.1.Коефіцієнт кореляції. Кореляційні функції.
При вирішенні багатьох задач радіоелектроніки часто виникають питання такого плану:
Один сигнал перевищує інший. Що при цьому мається на увазі?
Чи можливо об’єктивно оцінювати наскільки схожі два сигнали?
З
Рис.8.
7

![]() та
та
![]() .
Яку складову має вектор
у напрямку вектора
?
Складова
у напрямку
дорівнює
.
Яку складову має вектор
у напрямку вектора
?
Складова
у напрямку
дорівнює
![]() .
Тоді
.
Тоді
![]() , де
, де
![]() - вектор похибки (рис.8.7,а.)
Проте це не єдиний спосіб знаходження
складової вектора у певному напрямку
(рис.8.7,б,
рис.8.7,в.).
Яка ж відмінність між запропонованими
трьома способами подання вектора?
Вектор похибки на рисунку 8.7,а
виявляється
найменшим. Тепер можна сформулювати
кількісне визначення складової одного
вектора у напрямку іншого Складова
вектора
у напрямку вектора
визначається величиною
,
де
- вектор похибки (рис.8.7,а.)
Проте це не єдиний спосіб знаходження
складової вектора у певному напрямку
(рис.8.7,б,
рис.8.7,в.).
Яка ж відмінність між запропонованими
трьома способами подання вектора?
Вектор похибки на рисунку 8.7,а
виявляється
найменшим. Тепер можна сформулювати
кількісне визначення складової одного
вектора у напрямку іншого Складова
вектора
у напрямку вектора
визначається величиною
,
де
![]() підбирається так, щоб вектор похибки
був мінімальним. Очевидно, що чим більша
складова одного вектора на інший, тим
менша відмінність у напрямках обох
векторів і тим меншою буде вектор похибки
а
вказує на ступінь схожості двох векторів.
При цьому
підбирається так, щоб вектор похибки
був мінімальним. Очевидно, що чим більша
складова одного вектора на інший, тим
менша відмінність у напрямках обох
векторів і тим меншою буде вектор похибки
а
вказує на ступінь схожості двох векторів.
При цьому
 .
Якщо
.
Якщо
![]() то говорять що вектори
та
ортогональні і незалежні (зовсім не
схожі).
то говорять що вектори
та
ортогональні і незалежні (зовсім не
схожі).
Аналогічні
міркування будуть справедливі і до
складової вектора
у напрямку вектора
:
![]() ,
де -
,
де -
 .
.
Мірою
схожості двох векторів вважають величину
![]() яка є середнім геометричним між
яка є середнім геометричним між
![]() та
та
![]() :
:
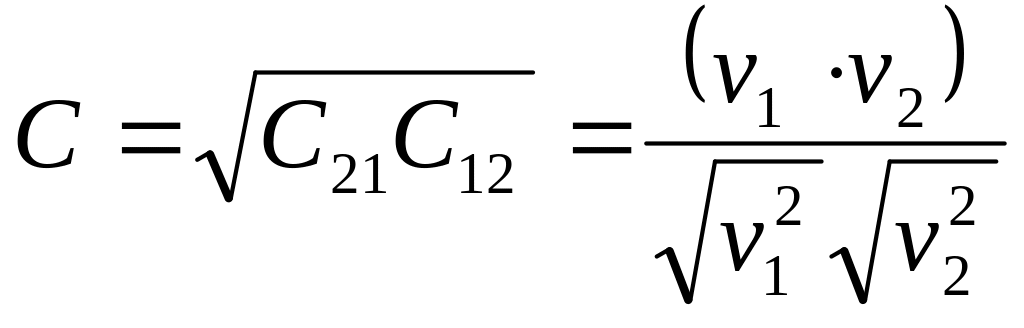 .
.
Очевидно, що величина С дорівнює косинусу кута між векторами і її модуль може знаходитися в межах від 0 до 1.
Поняття
про схожість векторів та їх ортогональність
можна застосувати і до сигналів.
Розглянемо два сигнали
![]() та
та
![]() . Необхідно апроксимувати сигнал
сигналом
на
заданому проміжку часу
. Необхідно апроксимувати сигнал
сигналом
на
заданому проміжку часу
![]() тобто
тобто
![]() .
Як вибрати
щоб апроксімація була найкращою? Очевидно
так, щоб похибка
.
Як вибрати
щоб апроксімація була найкращою? Очевидно
так, щоб похибка
![]() між
та
між
та
![]() була мінімальною:
була мінімальною:![]() .
Критерій мінімальності? Середнє значення
на проміжку
повинно бути мінімальним:
.
Критерій мінімальності? Середнє значення
на проміжку
повинно бути мінімальним:
 .
Проте такий критерій дозволяє значні
додатні та від’ємні похибки, що можуть
компенсувати друг друга і приводити до
фальшивого результату. Наприклад, при
апроксімації гармонічного сигналу
.
Проте такий критерій дозволяє значні
додатні та від’ємні похибки, що можуть
компенсувати друг друга і приводити до
фальшивого результату. Наприклад, при
апроксімації гармонічного сигналу
![]() функцією
функцією
![]() на інтервалі
на інтервалі
![]() :
:
![]()
![]() .
.
А хіба схожі ці два сигнали?
Тому для мінімізації відхилення одного сигналу від іншого запропонували використовувати середнє від квадрата похибки
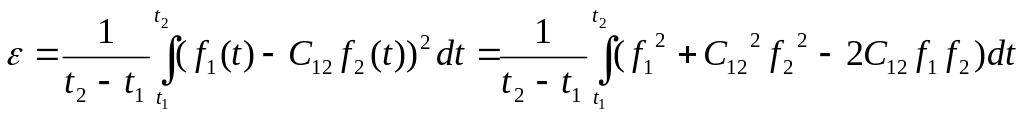
Яким
чином вибрати
,
щоб
![]() було мінімальним?
було мінімальним?
 .
.
Звідси
 .
.
Зверніть
увагу на схожість формул для знаходження
для векторів та функцій. По аналогії
 називається скалярним добутком двох
функцій
називається скалярним добутком двох
функцій
![]() та
та
![]() .
А коли їх скалярний добуток дорівнює
нулеві то функції називаються
ортогональними.
.
А коли їх скалярний добуток дорівнює
нулеві то функції називаються
ортогональними.
Можна
апроксимувати сигнал
сигналом
на проміжку
тобто
![]() .
І якщо
виберемо так, що
.
І якщо
виберемо так, що
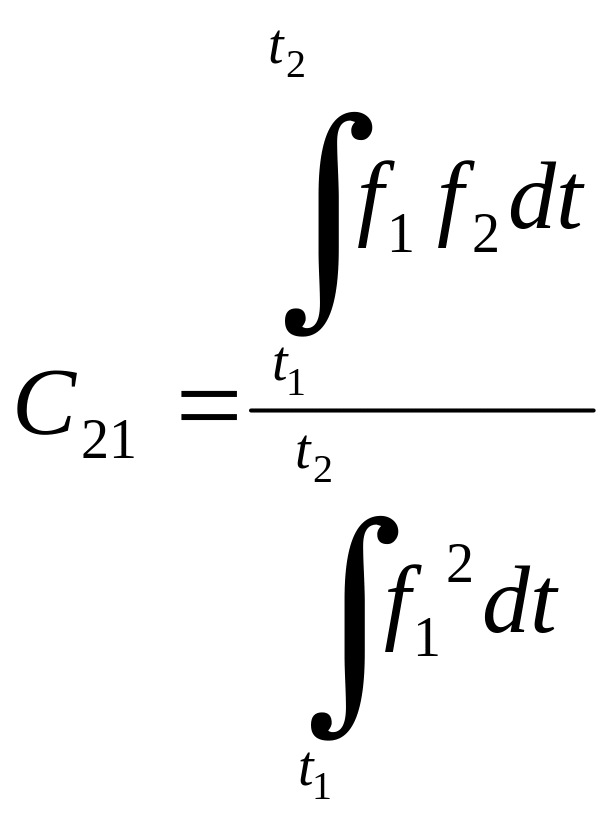 ,
,
то середнє від квадрата похибки буде мінімальним.
Середнє геометричне
від
та
є мірою схожості двох сигналів і
називається коефіцієнтом кореляції
![]() :
:
 .
(8.5)
.
(8.5)
Скориставшись
відомою нерівністю Коші-Буняковського
 ,
приходимо до висновку , що модуль
коефіцієнта кореляції може лежати лише
в інтервалі значень від 0 до 1.
,
приходимо до висновку , що модуль
коефіцієнта кореляції може лежати лише
в інтервалі значень від 0 до 1.
Радикали, що стоять
у знаменнику виразу (8.5) звуться нормами
функцій
![]() та
та
![]() :
:
 ,
,  .
.
Вони необхідні для того, щоб при порівнянні функцій та врахувати їх абсолютне значення і зрівняти їх за інтенсивністю. Якщо заздалегідь поділити функції та на їх норми, то одержимо нормовані значення цих функцій
![]()
![]() .
.
Для нормованих сигналів коефіцієнт кореляції набуває вигляду
 .
(8.6)
.
(8.6)
У теорії сигналів велику роль відіграють автокореляційні функції (АКФ)
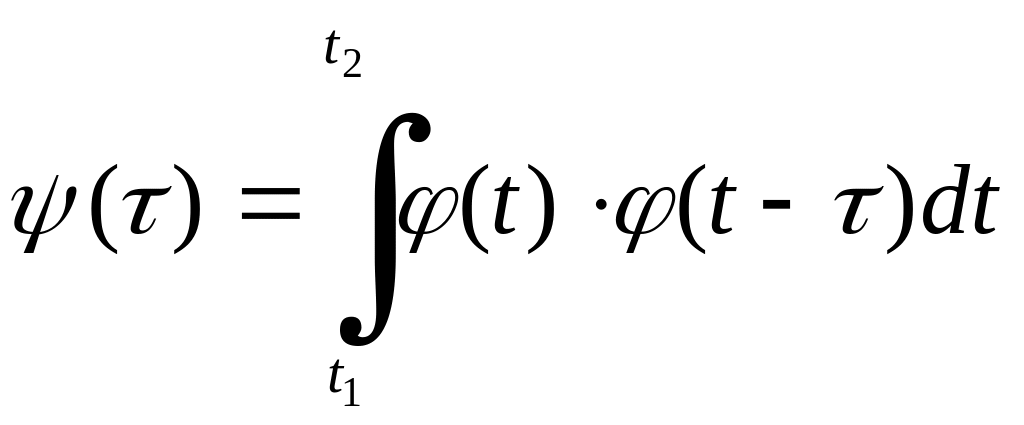 (8.7)
(8.7)
Зміст
автокореляційної функції полягає у
тому , що вона дає кількісну функціональну
міру зміни самої функції за проміжок
часу
![]() .
Цілком
очевидно, що
.
Цілком
очевидно, що
![]() .
. Можна також довести, що
.
. Можна також довести, що
![]() ,
тобто АКФ завжди є парною функцією.
Нормована АКФ може приймати значення
від
,
тобто АКФ завжди є парною функцією.
Нормована АКФ може приймати значення
від![]() до
до
![]() .
Значення
вона набуває, якщо
.
Значення
вона набуває, якщо
![]() ,
тобто якщо при зсуві на
,
тобто якщо при зсуві на
![]() функція
дорівнює
функція
дорівнює
![]() ,
але з протилежними знаком (так звана
антикореляція).
,
але з протилежними знаком (так звана
антикореляція).
Для періодичних
функцій інтегрування слід проводити в
межах періоду. Через ціле число періодів
АКФ для періодичної функції завжди
дорівнює одиниці:
![]() .
.
Так, наприклад,
для гармонічної функції
![]() норма дорівнює
норма дорівнює
![]() ,
і нормована АКФ буде
,
і нормована АКФ буде
![]()
