8.1. Динамічне представлення сигналів.

П

Рис.8. 2

ри динамічному представлені в основному використовують два типи елементарних сигналів: східчаста функція та прямокутні імпульси (див. рис.8.2).

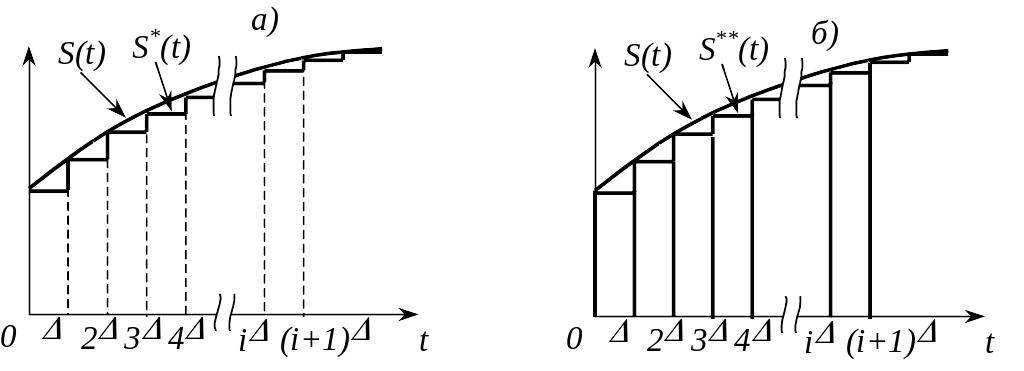
Математичною моделлю таких елементарних сигналів є функція включення або функція Хевісайда та дельта функція Дірака. З функціями такого типу має справу теорія узагальнених функцій, в якій функції визначаються як границі послідовностей і всі операції над ними розглядаються як операції над послідовностями.

Як вводиться функція Хевісайда ? Розглянемо функцію

Г

Рис.8. 3

рафік цієї функції показаний на рис.8.3,а.

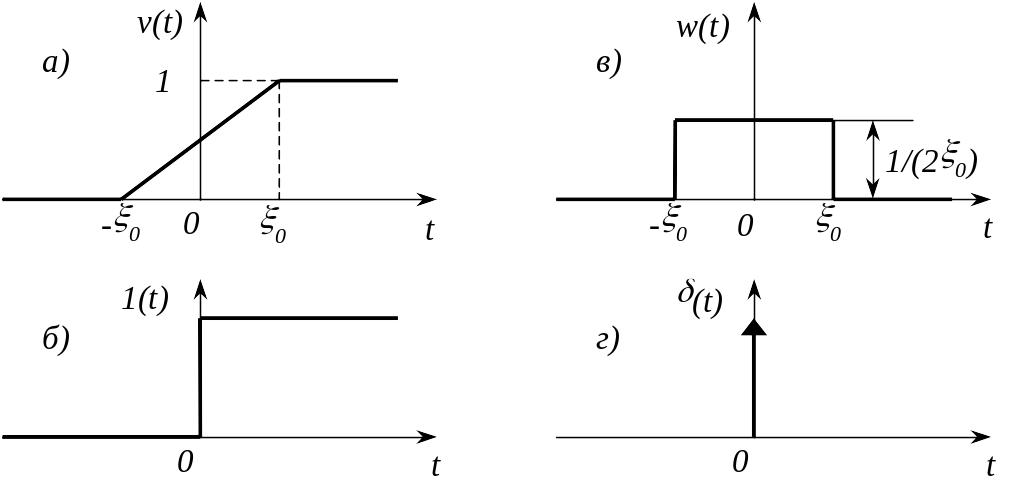
Тоді . Графічно функція Хевісайда показана на рис.8.3,б.

функція Дірака являється граничною функцією від (рис.8.3,в), де

Причому площа під графіком - дорівнює одиниці при будь якому .Тоді , а .

Якщо так, то , а . Графічно функція Дірака позначається так як показано на рис.8.3,г.

Повернемося до подання сигналу у вигляді суперпозиції елементарних сходинок. Розглянемо функцію яка наближено відтворює сигнал функціями Хевісайда

.

Очевидно, що . Якщо ввести нову змінну то , а . Тоді

(8.1)

Вираз (8.1) є однією із форм подання сигналу у вигляді суперпозицій функцій Хевісайда.

Якщо інтеграл у (8.1) взяти по частинам і скористатись тим, що , то

. (8.2)

Останній вираз і означає, що сигнал є суперпозицією елементарних імпульсів.

8.1.1.Імпульсні та перехідні характеристики лінійних систем.

П

Рис.8. 4

ерехідною характеристикою кола називається реакція кола на вхідний сигнал у вигляді функції Хевісайда (див. рис.8.4). Нехай коло стаціонарне , тобто якщо вхідний сигнал зсунутий у часі на величину то і вихідний сигнал з’явиться з точно таким же запізненням. Зокрема, якщо на вході існує сигнал то він породжує на виході сигнал

Чудова властивість лінійних систем - принцип суперпозиції - відкриває прямий шлях до систематичного розв’язку задач проходження різноманітних сигналів через такі системи. Оскільки вхідний сигнал можна подати у вигляді суперпозиції елементарних сходинок (8.1), то вихідний сигнал для стаціонарного кола буде такою ж лінійною комбінацією тільки вже перехідних характеристик. Тобто , якщо вхідний сигнал

,

то вихідним буде сигнал

. (8.3)

Ф

Рис.8. 5

ормула (8.3) має фундаментальне значення в теорії лінійних систем і називається інтегралом Дюамеля.

Реакцію кола на вхідний сигнал у вигляді функції Дірака називають імпульсною перехідною характеристикою і позначають як (рис.8.5). Якщо врахувати, що коло стаціонарне і , то отримаємо

. (8.4)

Інтеграл (8.4) називається інтегралом згортки і використовується при знаходженні реакції кола на вплив довільної форми .

Таким чином, якщо відома імпульсна перехідна або перехідна характеристики кола то з допомогою інтегралу Дюамеля або інтегралу згортки можна знайти вихідний сигнал.

Перехідну та імпульсну перехідну характеристики конкретного кола можна без ускладнень знайти з допомогою операторного метода. Нехай , тоді , а зображення вихідної величини тоді буде дорівнювати . Тому - це оригінал останньої функції. Аналогічно при - , а , і обернене перетворення Лапласа дає . Таким чином імпульсна перехідна характеристика кола є оригіналом операторної передаточної функції .

П

Рис.8. 6

риклад 8.1. Знайти напругу на виході послідовного RC-ланцюка при подачі на його вхід лінійно зростаючої напруги. За вихідну напругу вважайте напругу на конденсаторі. Графік вхідної напруги наведений на рис.8.6.

Рішення. Скористаємося інтегралом Дюамеля. Оскільки при і при , то у будь­-якій точці при . Для знаходження перехідної характеристики кола скористаємося операторним методом. Операторний коефіцієнт передачі для заданого кола - (тут - постійна часу кола). Таким чином зображення перехідної характеристики буде рівним - . Для знаходження перехідної характеристики скористаємося другою фомулою Хевісайда: . Отже .

Підставимо отримані значення у інтеграл Дюамеля (8.3):

.

Обчислюємо інтеграл: .

Звідки - .

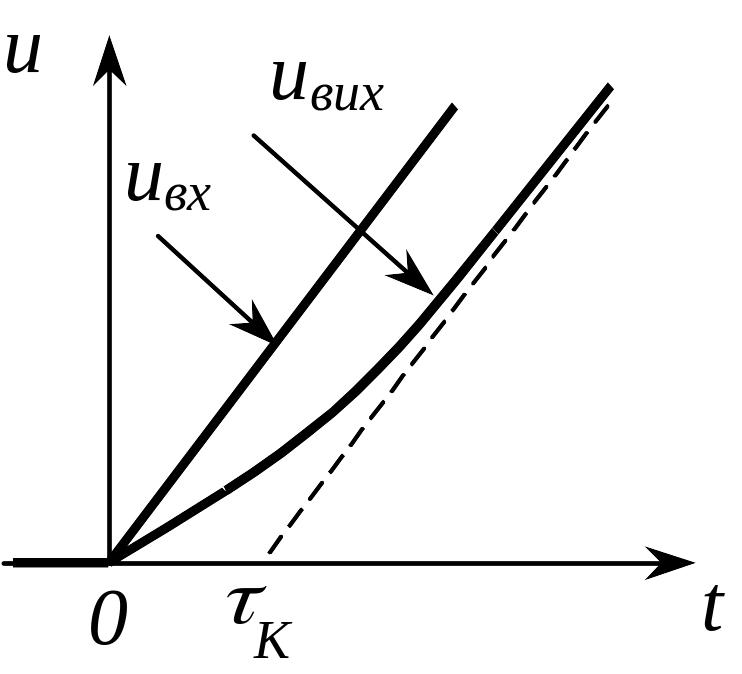
Графік залежності наведений на рис.8.6 Отже, з часом, напруга на конденсаторі наближається до лінійного закону, зсунутого у часі на величину відносно вхідної напруги.