
- •2. Поток векторного поля через поверхность. Его механический смысл
- •§ 3. Теорема Остроградского (векторная форма). Дивергенция векторного поля и её механический смысл
- •§ 4. Соленоидальное векторное поле и его свойства.
- •§ 5. Циркуляция векторного поля по замкнутому контуру. Вихрь векторного поля. Векторная форма теоремы Стокса.
- •§ 6. Потенциальное векторное поле
Разделяя переменные, получим
![]() .
Откуда следует общий интеграл уравнения
.
Откуда следует общий интеграл уравнения
![]() .
Учитывая, что интегральная кривая
проходит через точку
.
Учитывая, что интегральная кривая
проходит через точку
![]() ,
имеем
,
имеем
![]() .
Итак, векторная линия, проходящая через
точку
.
Итак, векторная линия, проходящая через
точку
![]() ,
представляет собой окружность
,
представляет собой окружность
![]() .
.
2. Поток векторного поля через поверхность. Его механический смысл
П
рис. 5


![]()
![]()
![]()

![]()







![]()
![]()
![]()

![]()
![]() находится двухсторонняя поверхность
.
Выберем на ней элементарную площадку,
площадь которой равна
.
Выберем на ней определённую сторону и
пусть нормаль, соответствующая выбранной
стороне поверхности, есть
.
Будем считать, что в пределах выбранной
площадки вектор
постоянен, обозначим через
находится двухсторонняя поверхность
.
Выберем на ней элементарную площадку,
площадь которой равна
.
Выберем на ней определённую сторону и
пусть нормаль, соответствующая выбранной
стороне поверхности, есть
.
Будем считать, что в пределах выбранной
площадки вектор
постоянен, обозначим через
![]() проекцию вектора
на направление нормали
(рис. 5).
проекцию вектора
на направление нормали
(рис. 5).
Определение.
Элементарным потоком векторного
поля
через площадку
в выбранную сторону называется
![]() .
.
Разбивая поверхность
на ячейки и суммируя элементарные потоки
вектора
по всем частичным ячейкам при условии,
что ранг дробления стремится к нулю,
получим
![]() ;
;
![]() называется потоком векторного поля
через поверхность
в выбранную сторону.
называется потоком векторного поля
через поверхность
в выбранную сторону.
Выясним теперь механический смысл потока векторного поля (рис. 5).
Допустим, что указанная выше поверхность
лежит в векторном поле
![]() скоростей текущей жидкости. Тогда за
время
скоростей текущей жидкости. Тогда за
время
![]() ,
исходя из данного момента времени
,
исходя из данного момента времени
![]() ,
частицы жидкости продвинутся через
элементарную площадку и заполнят
наклонный цилиндр, основанием которого
является элементарная площадка, а высота
,
частицы жидкости продвинутся через
элементарную площадку и заполнят
наклонный цилиндр, основанием которого
является элементарная площадка, а высота
![]() ,
если векторы
,
если векторы
![]() и
лежат в одном полупространстве. Масса
частиц жидкости, заполнявших этот
цилиндр,
и
лежат в одном полупространстве. Масса
частиц жидкости, заполнявших этот
цилиндр,
![]() ,
где
,
где
![]() - плотность текущей жидкости. Выполняя
суммирование всех этих масс по всей
поверхности
,
получим
- плотность текущей жидкости. Выполняя
суммирование всех этих масс по всей
поверхности
,
получим
 .
.
Правая часть этого соотношения даёт
нам количество жидкости, протекающей
через поверхность
за время
,
тогда очевидно, что выражение
![]() даёт нам количество жидкости, протекающей
через поверхность
в выбранную сторону за единицу времени.
В этом и заключается механический смысл
потока векторного поля.
даёт нам количество жидкости, протекающей
через поверхность
в выбранную сторону за единицу времени.
В этом и заключается механический смысл
потока векторного поля.
§ 3. Теорема Остроградского (векторная форма). Дивергенция векторного поля и её механический смысл
Рассмотрим поле вектора
![]() .
.
Определение. Дивергенцией векторного поля называется выражение
![]() .
.
Очевидно,
что с помощью оператора Гамильтона
дивергенцию можно записать так:
![]() .
.
Теорема Остроградского (векторная форма).
Поток
векторного поля
через замкнутую поверхность
наружу равен тройному интегралу от
дивергенции векторного поля
по телу
![]() ,
ограниченному поверхностью
,
т.е. короче:
,
ограниченному поверхностью
,
т.е. короче:
![]() .
.
Доказательство. Мы будем предполагать, что выполняются условия, при которых существуют интегралы, о которых речь пойдёт ниже.
Рассмотрим поток векторного поля через поверхность наружу: , где - есть внешняя нормаль к поверхности , ограничивающей тело , - проекция вектора на эту нормаль.
Пусть
нормаль
образует углы
![]() ,
,
![]() ,
,
![]() с координатными осями
с координатными осями
![]() ,
,
![]() и
и
![]() соответственно, тогда
соответственно, тогда
![]() ,
где
,
где
![]() - есть орт, соответствующий вектору
и при этом
- есть орт, соответствующий вектору
и при этом
![]() .
Тогда поток
можно выразить так:
.
Тогда поток
можно выразить так:
![]() .
.
Воспользуемся теперь формулой, устанавливающей связь между поверхностными интегралами первого и второго рода, тогда выражение для потока можно записать так:
![]() .
.
Вспоминая, что под знаком тройного интеграла в правой части стоит дивергенция векторного поля , тогда окончательно можно написать
![]() .
.
Выясним теперь механический смысл дивергенции векторного поля.
Допустим,
что векторное поле есть поле скоростей
текущей жидкости
и пусть плотность этой жидкости
![]() .
Возьмём в поле вектора
замкнутую поверхность
,
ограничивающую малый объём. По теореме
Остроградского
.
Возьмём в поле вектора
замкнутую поверхность
,
ограничивающую малый объём. По теореме
Остроградского
![]() .
.
Применяя
теорему о среднем, получим
![]() ,
где
,
где
![]() -некоторая "средняя точка", лежащая
в теле
.
Отсюда
-некоторая "средняя точка", лежащая
в теле
.
Отсюда
![]() .
.
Сжимая тело в точку, в пределе проучим
 .
.
Вывод:
дивергенция векторного поля
даёт нам расход жидкости из точечного
источника в единицу времени, т.е. удельную
силу источника. Заметим, что если
![]() в данной точке положительна, то это
значит, что в этой точке происходит
втекание жидкости (т.е. в этой точке
сток).
в данной точке положительна, то это
значит, что в этой точке происходит
втекание жидкости (т.е. в этой точке
сток).
Принимая во внимание это рассуждение, можно дать механическое истолкование теоремы Остроградского:
расход жидкости из тела , ограниченного поверхностью , в единицу времени равен сумме попарных произведений сит источников.
Заметим, что попутно мы доказали независимость дивергенции векторного поля от выбора системы координат. Действительно, с одной стороны
 ,
,
а с другой - это удельная сила источника, а независимость последней от системы координат очевидна.
П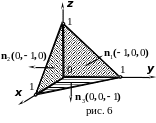 ример.
Найти поток векторного поля
ример.
Найти поток векторного поля
![]() из тела, ограниченного координатными
плоскостями
из тела, ограниченного координатными
плоскостями
![]() ,
,
![]() ,
,
![]() и плоскостью
и плоскостью
![]() наружу по теореме Остроградского и
непосредственно (рис. 6).
наружу по теореме Остроградского и
непосредственно (рис. 6).
Решение.
1-й метод решения. Вычислим поток
векторного поля по теореме Остроградского.
Найдём
![]() .
.
Имеем:
![]() ,
,
![]() ,
,
![]() .
Значит,
.
Значит,
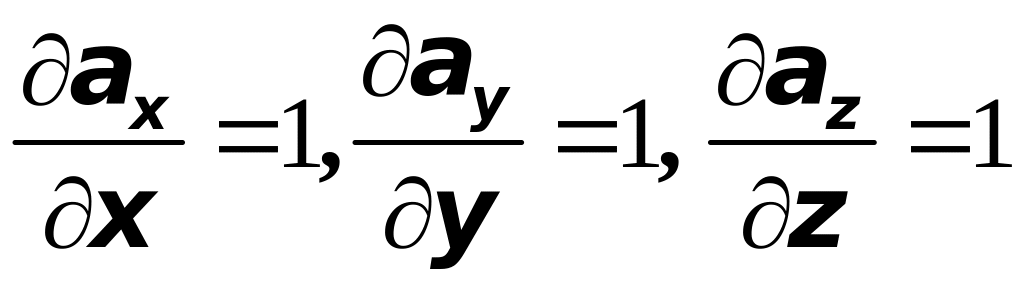 ,
,
Следовательно,
![]() .
.
Поток
векторного поля
 .
.
2-й метод решения. Вычислим поток векторного поля с помощью интеграла первого рода.
Имеем:
![]() ,
где
полная поверхность тела
,
состоящая из четырёх частей:
,
где
полная поверхность тела
,
состоящая из четырёх частей:
![]() ;
здесь
;
здесь
![]() ,
,
![]() и
и
![]() - направляющие косинусы внешней нормали
к поверхности;
- направляющие косинусы внешней нормали
к поверхности;
, , .
Поток можно представить в виде суммы четырёх потоков:
![]() .
Вычислим каждый из потоков:
.
Вычислим каждый из потоков:
1.
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
![]() ,
т.к. на поверхности
,
т.к. на поверхности
![]() .
.
2.
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
.
,
.
Таким образом:
![]() .
Здесь
.
Здесь
![]() ,
причём
на
,
причём
на
![]() ,
следовательно,
,
следовательно,
 .
.
3.
![]() ,
,
![]() ,
т.е.
,
т.е.
,
,
![]() ,
,
![]() ,
т.к. на поверхности
,
т.к. на поверхности
![]() .
.
4.
![]() .
.
Поверхность
![]() имеет уравнение
имеет уравнение
![]() ,
следовательно,
,
следовательно,
 ,
,
тогда
![]() .
Поверхностный интеграл здесь вычисляется
по верхней стороне поверхности
,
значит направляющие косинусы нормали
.
Поверхностный интеграл здесь вычисляется
по верхней стороне поверхности
,
значит направляющие косинусы нормали
![]() будут равны:
будут равны:
 .
.
Тогда получим

![]() .
.
Окончательно:
![]() .
.
3-й
метод решения. Вычислим тот же
самый поток с помощью поверхностного
интеграла второго рода
![]() .
.
В нашем
случае
![]() ,
как и в предыдущем случае, поток
представим в виде суммы четырёх потоков
соответственно, через поверхности
,
,
,
:
,
как и в предыдущем случае, поток
представим в виде суммы четырёх потоков
соответственно, через поверхности
,
,
,
:
1. На
,
![]() ,
а значит
,
а значит
![]() .
.
2. На
,
![]() ,
а сторона поверхности, по которой
вычисляется интеграл, нижняя, значит
,
а сторона поверхности, по которой
вычисляется интеграл, нижняя, значит

3. На
,
![]() ,
сторона поверхности нижняя значит
,
сторона поверхности нижняя значит
![]() .
.
4.
![]()
![]() .
.
На
![]() .
.
Следовательно,

![]() .
.
