
- •§ 2. Тройной интеграл
- •1. Определение тройного интеграла
- •2. Вычисление тройного интеграла
- •3. Геометрический смысл тройного интеграла
- •§ 3. Приложения двойных и тройных интегралов
- •5. Вычисление массы тела
- •6. Моменты плоской фигуры
- •7. Координаты центра масс
- •§ 4. Криволинейные координаты и замена переменных в кратных интегралах
- •1. Криволинейные координаты
- •2. Координатные поверхности
- •3. Координатные линии
- •4. Коэффициенты Ламе
- •5. Сферические координаты
4. Коэффициенты Ламе
Рассмотрим
вектор
- радиус-вектор точки
(рис. 13). Очевидно, что производная
![]() лежит на касательной к годографу вектора
,
построенному в предположении, что
меняется только координата
,
а координаты
и
остаются неизменными в сторону возрастания
координаты
.
Очевидно, что
лежит на касательной к годографу вектора
,
построенному в предположении, что
меняется только координата
,
а координаты
и
остаются неизменными в сторону возрастания
координаты
.
Очевидно, что
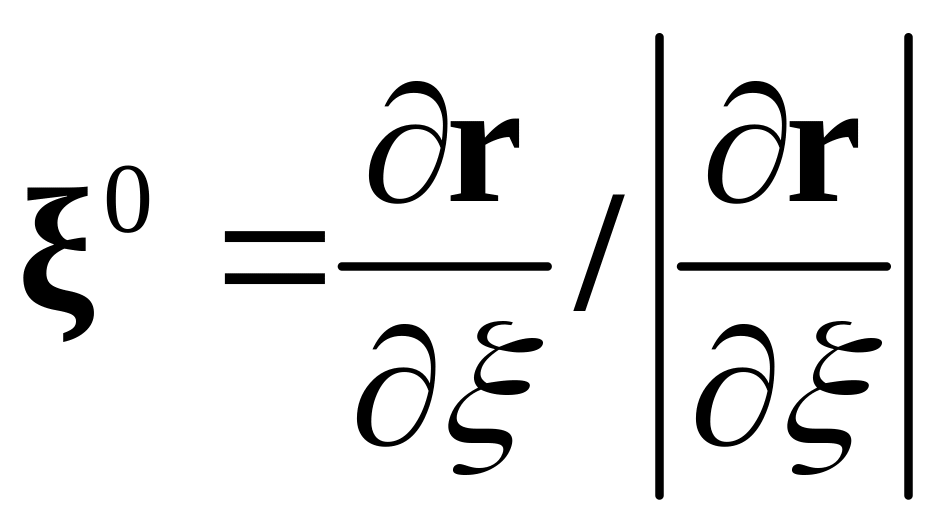 .
.
Аналогично
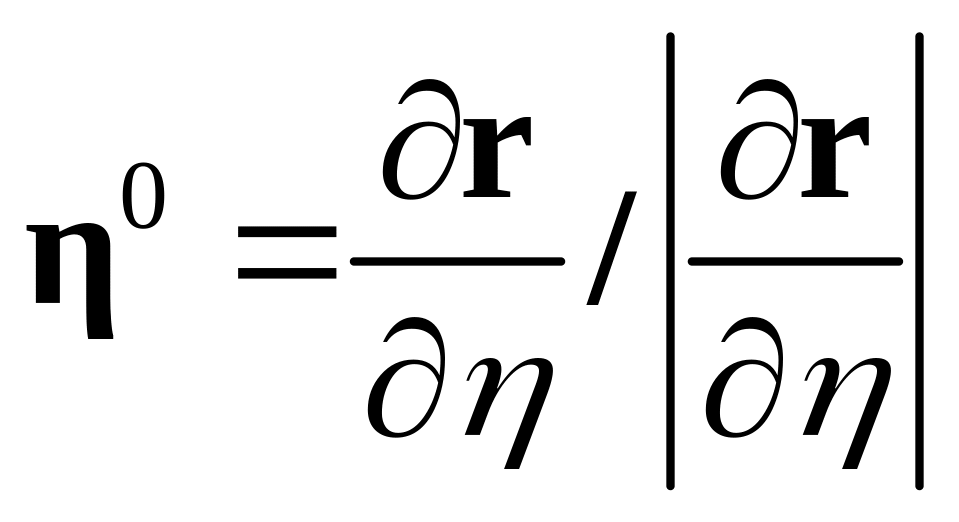 ,
,
 .
.
Выражения
 называются коэффициентами Ламе. Так
как радиус-вектор точки
.
называются коэффициентами Ламе. Так
как радиус-вектор точки
.
![]() ,
то, выполняя дифференцирование, получим
,
то, выполняя дифференцирование, получим
 (4)
(4)
Принимая во внимание эти соотношения, нетрудно получить такие выражения для коэффициентов Ламе:
![]() (5)
(5)
Примем во внимание соотношения (4) и (5), тогда выражение для ортов криволинейных координат запишутся так:

5. Сферические координаты
С
ферическими
координатами точки
называются параметры
,
![]() и
(рис. 14), где
и
(рис. 14), где
![]()
![]()
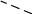
 - расстояние от точки
до начала координат
- расстояние от точки
до начала координат
![]()

 - угол, отсчитываемый от оси
до вектора
- угол, отсчитываемый от оси
до вектора
![]() ;
;
рис. 14

![]()

 - угол между плоскостью
и плоскостью, проходящей через точку
и ось
(
- угол между плоскостью
и плоскостью, проходящей через точку
и ось
(![]() ).
).
Очевидно,
что в сферических координатах координатными
поверхностями являются также
поверхности : -
![]() - сфера радиуса
- сфера радиуса
![]() с центром в начале координат;
с центром в начале координат;
![]() - конус с вершиной в начале координат,
образующие которого составляют угол
с осью
;
- конус с вершиной в начале координат,
образующие которого составляют угол
с осью
;
![]() - плоскость, проходящая через ось
и образующая угол
- плоскость, проходящая через ось
и образующая угол
![]() с координатной плоскостью
.
с координатной плоскостью
.
Сфера
и конус
пересекаются по окружности, которая
представляет собой координатную
линию
.
Сфера
и плоскость
![]() пересекаются по окружности (координатная
линия
).
Конус
и плоскость
пересекаются по прямой (координатная
линия
).
Орты криволинейной сферической системы
координат изображены на рис. 14.
пересекаются по окружности (координатная
линия
).
Конус
и плоскость
пересекаются по прямой (координатная
линия
).
Орты криволинейной сферической системы
координат изображены на рис. 14.
Непосредственно из рис. 14 можно установить связь между декартовыми и сферическими координатами.
 .
.
