7. Координаты центра масс

Пусть - плоская область, в которой распределена масса с плотностью . По определению центром масс плоской области называется точка с координатами

,

где - масса плоской области , а и - статические моменты.

Принимая во внимание выражения для массы и статических моментов через двойные интегралы, получим

Рассмотрим теперь некоторое тело , ограниченное простой поверхностью, и пусть в нём распределена масса, плотность которой , то для координат центра масс этого тела получим совершенно аналогичные выражения:

.

§ 4. Криволинейные координаты и замена переменных в кратных интегралах

1. Криволинейные координаты

О

рис. 12

тносительно пространственной декартовой системы координат положение точки определяется её тремя декартовыми координатами , и . Если , то положение точки можно определить, задав такие три параметра: - расстояние точки от оси ; -расстояние точки от начала координат; - двухгранный угол между плоскостью и плоскостью,

проходящей через ось и точку (рис. 12). Очевидно, что параметры , и можно выразить через декартовы координаты и . Параметры , и мы можем также назвать координатами точки , .

И вообще, за координаты точки мы можем принять любые три функции:

(1)

лишь бы только соотношениями (1) координаты и определялись однозначно:

(2)

Т.е. ни одно из соотношений (1) или (2) не должно противоречить другим или быть следствием других. Заметим, что из соотношений (2) в этом случае параметры и также будут определяться однозначно. Можно доказать, что эти условия выполняются, если определить , называемый определителем Якоби или якобианом преобразования, отличен от нуля, т.е.

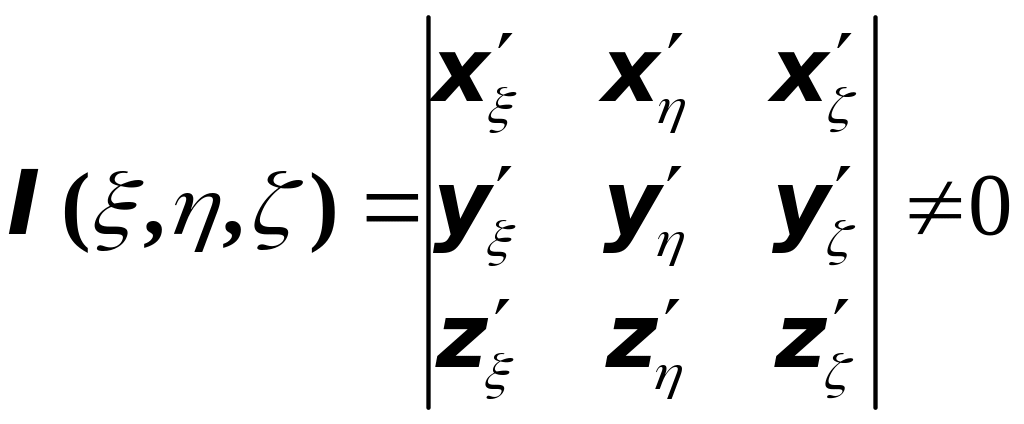(3)

2. Координатные поверхности

Зафиксируем какую-нибудь координату, определённую соотношениями (1), например , положив , тогда получим (рис. 13).

С геометрической точки зрения этому уравнению в пространстве соответствует некоторая поверхность . Аналогично можно определить координатные поверхности и соответственно:

и .

Координатные поверхности , и при соблюдении условия (2) пересекаются в некоторой точке . Таким образом, точка определяется как точка пересечения координатных поверхностей (рис. 13).

3. Координатные линии

Р ассмотрим пересечения двух координатных поверхностей

.

О

рис. 13

чевидно, что кривая, по которой пересекаются эти поверхности, обладает таким свойством, что вдоль этой кривой координаты и постоянны, а меняется одна только координата , поэтому эта кривая называется координатной линией . Аналогично пересечение поверхностей

и

даёт нам соответственно координатные линии и .

Очевидно, что в общем случае координатные линии представляют собой некоторые кривые, поэтому координаты и называются криволинейными координатами. Проведем к координатным линиям, пересекающимся в точке , касательные, направления которых соответствуют направлениям возрастания координат. Орты этих осей называются ортами криволинейных координатных осей и обозначаются соответственно и . Систему криволинейных координат называют ортогональной, если ортогональны орты и , т.е. если выполняются условия

.

Заметим, что в декартовой системе координат координатными поверхностями будут являться плоскости, параллельные координатным плоскостям , а координатными линиями - прямые, параллельные осям и .