между нормалями и ним, т.е. , где - острый угол между нормалью к поверхности и осью . Тогда получим

Тогда, суммируя все такие элементарные площади и устремляя ранг дробления к нулю, получим окончательно

.

§ 2. Тройной интеграл

1. Определение тройного интеграла

Рассмотрим некоторую поверхность .

Определение 1. Поверхность называется простой поверхностью, если она распадается на конечное число частей, имеющих уравнение , или , или , причём функции и непрерывны в некоторой простой области .

В дальнейшем мы будем рассматривать пространственные области, ограниченные простыми поверхностями, мы будем выделять простые пространственные области, определения которых аналогично определению простой плоской области, рассмотренной выше.

Остановимся теперь на понятии объёма тела , ограниченного простой поверхностью . Для этого поместим тело целиком внутрь параллелепипеда, грани которого параллельны координатным плоскостям , и . Разобьём далее параллелепипед плоскостями, параллельными координатным плоскостям, на ячейки. Обозначим через сумму объёмов ячеек, целиком лежащих внутри тела и не имеющих ни одной общей точки с поверхностью , ограничивающей тело . Обозначим через сумму объёмов ячеек, имеющих с телом или его поверхностью хотя бы одну общую точку. Очевидно, что . Наибольший из диаметров ячеек назовём рангом дробления . Если существует общее значение

при условии, что число ячеек бесконечно увеличивается, а ранг дробления стремится к нулю, то число называется объёмом тела , а само тело называется кубируемым.

Дадим теперь определение тройного интеграла.

Рассмотрим некоторое тело , ограниченное простой поверхностью. Можно доказать, что такие тела кубируемы, т.е. имеют объём. И пусть в каждой точке этого тела задана функцию .

Определение 2. Разобьём тело (рис 10) простыми поверхностями на части с диаметрами и объёмами . Наибольший из диаметров называется рангом дробления .

В каждой частичной ячейке возьмём произвольную точку и вычислим в ней значение функции , которое умножим на объём соответствующей ячейки , т.е. составим произведения: .

Просуммируем все такие произведения, т.е. составим интегральную сумму (сумму Римана):

.

И змельчая дробление, будем искать предел последовательности интегральных сумм

.

Е сли этот предел существует и не зависит от способа дробления и выбора точки , то он называется тройным интегралом от функции по телу и обозначается так:

рис. 10

и .

Итак, лаконично можно сказать так: тройной интеграл есть предел последовательности интегральных сумм, т.е.

.

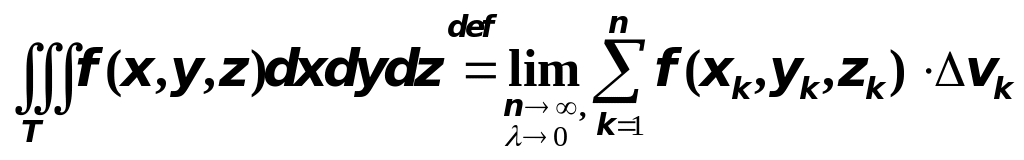Теорема существования тройного интеграла.

Если функция непрерывна в каждой точке тела , ограниченного простой поверхностью, то существует тройной интеграл от функции по телу .

(без доказательства)

Заметим, что свойства тройного интеграла аналогичны свойствам двойного интеграла и поэтому мы не будем отдельно останавливаться.

2. Вычисление тройного интеграла

Пусть тело есть простая область (рис. 10). Допустим, что оно ограничено снизу поверхностью , сверху поверхностью , а с боков - цилиндрической поверхностью, образующие которой параллельны оси , а направляющей служит граница простой области , расположенной в плоскости , причём функции и непрерывны в области . Пусть, кроме того, функция интегрируема в теле . Тогда можно сказать, что

,

причём интеграл, стоящий справа, записывается так:

.

В том случае, если область ограничена снизу непрерывной кривой , сверху - непрерывной кривой , а с боков прямыми и , то последнюю формулу можно записать так:

.

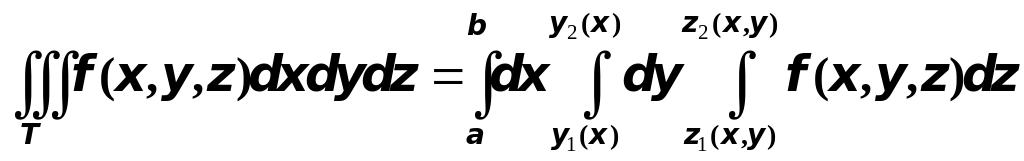Интеграл, стоящий справа, называется трехкратным или повторным. Заметим, что выбирая внешнее интегрирование по переменной или , можно написать ещё пять различных трехкратных интегралов, через которые выражается данный интеграл . Порядок выполнения операций интегрирования зависит от вида области, по которой выполняется интегрирование.