Содержание отчета

В отчете о лабораторной работе должны быть представлены:

• принципиальные схемы исследуемых ЭЦ и расчет заданных параметров ЭЦ;

• результаты моделирования ЭЦ с анализом полученных результатов по каждому пункту проведенных исследований.

4. Лабораторная работа № 8 Электрические фильтры

4.1. Основные сведения

Электрическими фильтрами называют электрические цепи, предназначенные для выделения колебаний, лежащих в определенном диапазоне частот. Диапазон частот, пропускаемых фильтром, называется полосой прозрачности или полосой пропускания. Остальная область частот, подавляемая фильтром, называется полосой задержания или полосой непрозрачности.

Н а рис. 4.1 приведены амплитудно-частотные характеристики (частотно-зависимые коэффициенты передачи по напряжению) идеальных фильтров. В зависимости от диапазона частот, пропускаемых фильтром, различают фильтры: нижних частот (ФНЧ) – полоса пропускания от 0 до некоторой частоты f_c (рис. 4.1, а), называемой частотой среза; верхних частот (ФВЧ) – полоса пропускания от f_c до ∞ (рис. 4.1, б); полосовые (ПФ) – полоса пропускания от f_c1 до f_c2 (рис. 4.1, в) и заграждающие или режекторные (РФ) – полоса задержания от f_c1 до f_с2 (рис. 4.1, г). Таким образом, коэффициент передачи идеального фильтра равен единице в полосе прозрачности и нулю – в полосе заграждения.

В зависимости от типов входящих в них элементов электрические фильтры подразделяются на реактивные (или LC-фильтры), RC-фильтры, активные фильтры и др. Рассмотрим основные свойства реактивных фильтров, т.е. фильтров, состоящих только из катушек индуктивности и конденсаторов с высокой добротностью (реактивных элементов без потерь).

Реактивные фильтры можно выполнить путем согласованного каскадного соединения отдельных звеньев, представленных в виде четырехполюсников (ЧП). На рис. 4.2 показан ЧП, нагруженный на сопротивление Z_н2 и подключенный к источнику напряжения с внутренним сопротивлением Z_Г. Простейшим типом звена является Г-образное звено, представляющее собой Г-образный ЧП с П- или Т-в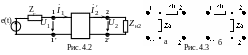 ходом (рис. 4.3). При согласованном каскадном соединении таких звеньев получаются симметричные П- или Т-образные звенья (рис. 4.4), причем Z₁ = 2Z_b , а Z₂ = Z_a/2.

П ри анализе характеристик четырехполюсников в случае их каскадного соединения удобно пользоваться основными уравнениями ЧП в А-форме:

или , (4.1)

где и – напряжения на входе и выходе ЧП, – ток, втекающий в узел 1, – ток, вытекающий из узла 2, а A= - матрица первичных А-параметров четырехполюсника, которые определяются в режиме холостого хода и короткого замыкания на выходе ЧП и имеют определенный физический смысл:

- величина, обратная коэффициенту передачи по напряжению при ХХ на выходе – 1/K_u(jω);

- передаточное сопротивление при КЗ на выходе;

- передаточная проводимость при ХХ на выходе;

- величина, обратная коэффициенту передачи по току при КЗ на выходе - 1/K_i(jω).

Матрицы A первичных параметров Г-образных звеньев с П- и Т-входом (рис. 4.2) соответственно имеют вид:

; . (4.2)

При каскадном соединении четырехполюсников матрица А-параметров составного ЧП равна произведению матриц А-параметров входящих в него элементарных ЧП. Поэтому матрицы А_П и А_Т приведенных на рис. 4.4 П- и Т-образных четырехполюсников равны:

А_П = А_Г1 · А_Г2; А_Т = А_Г2 · А_Г1. (4.3)

Подставив (4.3) в (4.2) с учетом принятых соотношений Z₁ = 2Z_b и Z₂ = Z_a/2, получим:

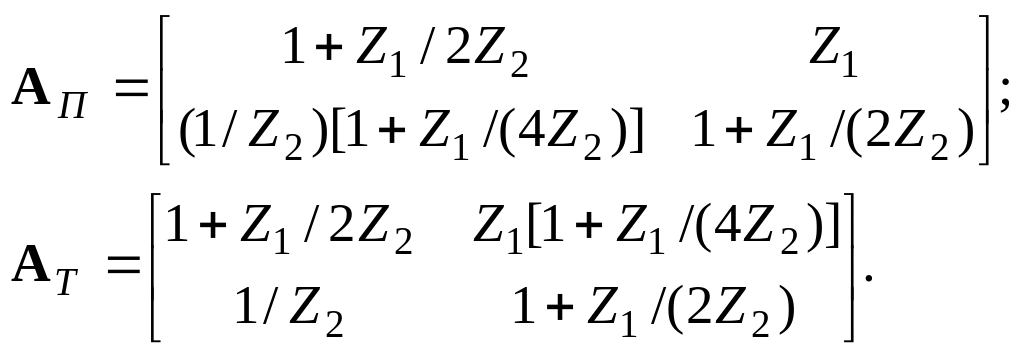(4.4)

Следует отметить, что в силу симметрии рассматриваемых П- и Т-четырехполюсников A₁₁ = A₂₂ = 1+Z₁/2Z₂. Для согласования ЧП с источником сигнала и нагрузкой определим характеристические параметры четырехполюсника.

Характеристическими сопротивлениями четырехполюсника называют пару сопротивлений Z_с1 и Z_с2, которые выбраны таким образом, что при подключении к зажимам 2-2’ сопротивления Z_н2 = Z_с2 входное сопротивление четырехполюсника со стороны зажимов 1-1’ равно Z_вх = Z_с2. И наоборот, при подключении к зажимам 1-1’ сопротивления Z_н1 = Z_с1 выходное сопротивление ЧП со стороны зажимов 2-2’ равно Z_вых = Z_с1. Входное и выходное характеристические сопротивления можно выразить через А-параметры [1]:

. (4.5)

Очевидно, что для симметричных четырехполюсников (A₁₁ = A₂₂) характеристические входное и выходное сопротивления одинаковы:

. (4.6)

При согласованной нагрузке симметричные ЧП имеют одинаковые значения коэффициентов передачи по напряжению и току :

. (4.7)

Другой важной характеристикой четырехполюсника является характеристическая постоянная передачи при прямом и обратном включениях ЧП Г₁ и Г₂ , которые в случае П- и Т-звена (рис. 4.4) равны между собой (Г₁ = Г₂ = Г) и описываются выражениями [1]:

(4.8)

Для симметричных ЧП коэффициенты передачи по току и напряжению связаны с характеристической постоянной передачи соотношениями [1]:

. (4.9)

В связи с тем, что , из (4.9) следует

. (4.10)

Величина A(ω) = Re(Г = ln(U₁/U₂) называется постоянной ослабления и определяет амплитудно-частотную характеристику (АЧХ)

, (4.11)

а величина B(ω) = Im(Г) называется постоянной фазы и определяет фазочастотную (ФЧХ) характеристику четырехполюсника

. (4.12)

Единицей измерения постоянной ослабления служит безразмерная величина – непер (Нп). При А = 1 Нп коэффициент передачи четырехполюсника (4.11) K_u(ω) = 1/e = 1/2,72, т.е. напряжение на выходе ЧП в e ≈ 2,72 раза меньше, чем на входе. Постоянную ослабления часто вычисляют не через натуральный логарифм, а через десятичный в децибелах (дБ): А = 20 lg(U₁/U₂).

При согласованном каскадном соединении произвольного числа N одинаковых симметричных четырехполюсников с характеристическими параметрами Z_с0 и Г₀ характеристическое сопротивление составного ЧП Z_с = Z_с0, а характеристическая постоянная передачи – Г = N·Г₀. Тогда коэффициент передачи по напряжению составного ЧП равен

, (4.13)

где - АЧХ и ФЧХ отдельного звена составного ЧП.

В фильтрах, содержащих П- и Т-образные звенья, которые называются фильтрами типа k, сопротивления Z₁ и Z₂ (которые имеют чисто реактивный характер: Z₁ = jx₁, Z₂ = jx₂) выбираются из условия

, (4.14)

вследствие чего - вещественная величина.

Учитывая, что , получаем:

(4.15)

В пределах полосы пропускания постоянная ослабления А=0, следовательно, shA = 0 и chA = 1. Тогда из (4.15) следует, что постоянная фазы B в полосе прозрачности изменяется по закону:

. (4.16)

За пределами полосы пропускания А ≠0 (shA ≠ 0), тогда из (4.15) следует, что sinB = 0 (значит, cosB = ±1), а chA = ±[1 +x₁/(2x₂)].

Поскольку cosB по абсолютному значению не может превышать единицу, соотношение между Z₁ и Z₂ в пределах полосы пропускания должно удовлетворять условию

. (4.17)

Неравенство (4.17) называется условием прозрачности фильтра. Очевидно, что для выполнения условия прозрачности (А = 0) реактивные сопротивления Z₁ и Z₂ должны иметь различные знаки, т.е. сопротивления поперечной и продольной ветвей фильтра имеют разный характер. Предельные (граничные) значения частоты, на которых выполняются условия прозрачности фильтра, являются границами полосы пропускания, а сопротивления Z₁ и Z₂ на этих частотах связаны соотношениями

(4.18)

Подставив в выражение для характеристического сопротивления симметричного ЧП (4.6) значения параметров А и А П- и Т-образных четырехполюсников (4.4), с учетом (4.14) получим:

. (4.19)

Из (4.19) следует, что характеристические сопротивления фильтров типа k имеют чисто резистивный характер и являются частотно-зависимыми. Поэтому невозможно согласовать фильтр в пределах всей полосы пропускания, вследствие чего характеристики реальных фильтров значительно отличаются от идеальных.

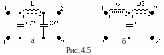На рис. 4.5 приведены П- и Т- образные фильтры нижних частот, в которых Z₁ =jωL и Z₂ = 1/jωC. Тогда условие (4.16) преобразуется к виду , и с учетом (4.18) получаем граничные частоты полосы пропускания ФНЧ (А = 0):

ω₁ = 0; . (4.20)

В полосе задержания (учитывая, что функция ch(x)≥1) постоянная ослабления А определяется соотношением

. (4.21)

График постоянной ослабления А (в децибелах) показан на рис. 4.6. Подставив в (4.19) значения Z₁ и Z₂, получим:

, (4.22)

где ; .

Из (4.22) следует, что при ω < ω_г, т.е. в полосе пропускания, Z_П и Z_Т являются активными сопротивлениями, которые изменяются с ростом частоты от значения k до ∞ у П-образного и до 0 у Т-образного фильтра. За пределами полосы пропускания (ω > ω_г) Z_П и Z_Т также частотно- зависимы и являются реактивными сопротивлениями. Таким образом, добиться работы фильтра на согласованную нагрузку (хотя бы в полосе прозрачности) невозможно. Изменение сигнала на выходе фильтра при несогласованной нагрузке оценивают коэффициентом затухания, выраженном в децибелах (дБ): а = 20 lg(U_вх/U_вых). График коэффициента затухания низкочастотного П-образного фильтра при сопротивлении нагрузки R_н = k показан на рис. 4.6. Сравнение кривых А и а на рис. 4.6 показывает, что в реальных условиях работы фильтра при постоянном сопротивлении нагрузки наблюдается подавление сигнала и в полосе пропускания, а в полосе задержания а < A.

П ри расчете фильтров типа k задают граничную частоту ω_г и сопротивление нагрузки R_н, которое должно быть равно k. Используя выражения (4.14) и (4.20), составим систему уравнений:

(4.23)

Решая систему уравнений (4.23) относительно параметров элементов фильтра, получаем:

. (4.24)

В ысокочастотные фильтры (ФВЧ) получаются из низкочастотных, если поменять местами конденсаторы и катушки индуктивности. Высокочастотные П- и Т-образные фильтры показаны на рис. 4.7.

П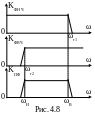 олосовые фильтры (ПФ) могут быть получены при каскадном соединении двух фильтров: ФНЧ и ФВЧ, имеющих соответственно граничные частоты ω_г1 и ω_г2. Причем должно выполняться условие ω_г1 > ω_г2. Поскольку коэффициент передачи составного ЧП при согласованном включении K(ω) = K_ФНЧ(ω)·K_ФВЧ(ω), то в соответствии с рис. 4.8 нижняя граничная частота ПФ ω_Н = ω_г2, а верхняя – ω_В = ω_г1.

При каскадном соединении нескольких однотипных (П- или Т-образных) фильтров необходимо учитывать правило вычисления сопротивления (проводимости) последовательно (параллельно) соединенных проводников. На рис. 4.9 показано соединение двух низкочастотных Т-образных звеньев. Следует о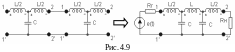 братить внимание, что внутреннее сопротивление генератора и нагрузки, подключаемых к составному четырехполюснику, равны

.

П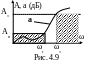 омимо реактивных фильтров типа k, существуют и другие фильтры (типа m, Баттерворта, Чебышева и др.). При синтезе фильтров стремятся, чтобы его характеристики минимально отличались от идеальных (рис. 4.1). Для этого задают максимально допустимое значение постоянной ослабления в полосе прозрачности А_п, неравномерность ΔА в полосе пропускания и минимально допустимое значение постоянной ослабления в полосе задержания А_з с указанием граничных частот ω_г полосы пропускания и частот среза ω_с полосы заграждения. В качестве примера на рис. 4.9 показаны трафарет задания частотной характеристики низкочастотного фильтра (выделен штриховкой) и возможная реализация коэффициента затухания реального фильтра (кривая а).

Для аналитического решения задачи реализации фильтра, отвечающего поставленным требованиям, необходимо выбрать функцию, которая с достаточной точностью удовлетворяет заданным условиям. В частности, в качестве аппроксимирующих функций используются полиномы Баттерворта (постоянная ослабления монотонно возрастает в полосе прозрачности) или Чебышева (в полосе пропускания характеристика А(ω) имеет колебательный характер) [2]. В настоящее время реактивные фильтры имеют весьма ограниченную область применения, однако теория таких фильтров не утратила прикладного значения, поскольку при построении многих типов современных фильтров (активных, цифровых) реактивные фильтры используются в качестве прототипов.