42

1. Лабораторная работа № 5 Переходные процессы в электрических цепях первого порядка

1.1. Основные сведения

Рассмотренные в первой части лабораторного практикума электрические цепи постоянного и переменного тока находились в установившемся режиме, т.е. параметры токов и напряжений во всех ветвях ЭЦ сохраняли неизменные значения с течением времени. Всякое изменение топологии цепи (подключение или отключение отдельных ветвей ЭЦ) или параметров входящих в нее элементов (пассивных элементов или источников энергии) приводит к тому, что режим работы цепи становится неустановившимся. Любое скачкообразное изменение в цепи (топологии цепи или параметров ее элементов), нарушающее установившийся режим, называется коммутацией. В результате коммутации наступает переходный процесс – процесс перехода электрической цепи из одного установившегося режима в другой.

Длительностью процесса коммутации, как правило, пренебрегают, т.е. считают, что коммутация осуществляется практически мгновенно. Начало отсчета времени переходного процесса обычно совмещают с моментом коммутации, причем момент времени, непосредственно предшествующий коммутации, обозначают через , а начальный момент времени непосредственно после коммутации – через .

Переходные процессы, связанные с изменением топологии цепи, присущи в основном устройствам производства, передачи и преобразования электрической энергии. Для радиотехнических устройств более характерен режим, когда топология цепи и параметры пассивных элементов неизменны, а внешнее воздействие на цепь изменяется по произвольному (в частности, по скачкообразному) закону. В идеальных резистивных ЭЦ процесс перехода от одного установившегося состояния к другому происходит мгновенно в момент коммутации. Однако реальные электрические цепи содержат реактивные элементы L и C (пусть даже паразитные L и C малой величины), которые способны запасать электрическую энергию в магнитном или электрическом полях:

. (1.1)

Поскольку каждому установившемуся состоянию соответствует определенное значение энергии, запасенной в электрическом и магнитном полях, то переходный процесс не может быть скачкообразным, т.к. скачкообразное изменение электрической энергии ЭЦ потребовало бы ее бесконечно большой мощности (P = dW/dt). Любой реальный источник энергии может отдавать только конечную мощность, поэтому суммарная энергия, запасенная в цепи, может изменяться только плавно, т.е. представляет собой непрерывную функцию времени.

С учетом вышесказанного и выражений (1.1) справедливы два закона коммутации [2].

Первый закон коммутации. В начальный момент времени после коммутации ток индуктивности сохраняет такое же значение, как и непосредственно перед коммутацией: , а затем плавно изменяется, начиная с этого значения.

Второй закон коммутации. В начальный момент времени после коммутации напряжение на емкости сохраняет такое же значение, как и непосредственно перед коммутацией: , а затем плавно изменяется, начиная с этого значения.

Законы коммутации не накладывают ограничений на характер изменения токов емкостей, напряжений индуктивностей, а также токов или напряжений сопротивлений, которые могут изменяться произвольным образом, в том числе и скачкообразно.

Задача анализа переходных процессов в общем случае заключается в определении мгновенных значений токов и напряжений всех или части ветвей ЭЦ в произвольный момент времени после коммутации и может быть решена классическим или операторным методом. Рассмотрим классический метод анализа переходных процессов

Как известно, система уравнений электрического равновесия цепи, полученная любым способом и содержащая искомые токи и напряжения ветвей ЭЦ, может быть путем дифференцирования и последовательного исключения неизвестных сведена к одному дифференциальному уравнению для любого из неизвестных токов или напряжений. Полученное уравнение называется дифференциальным уравнением цепи [2]. При составлении дифференциального уравнения пользуются известными соотношениями между током и напряжением на пассивных элементах цепи:

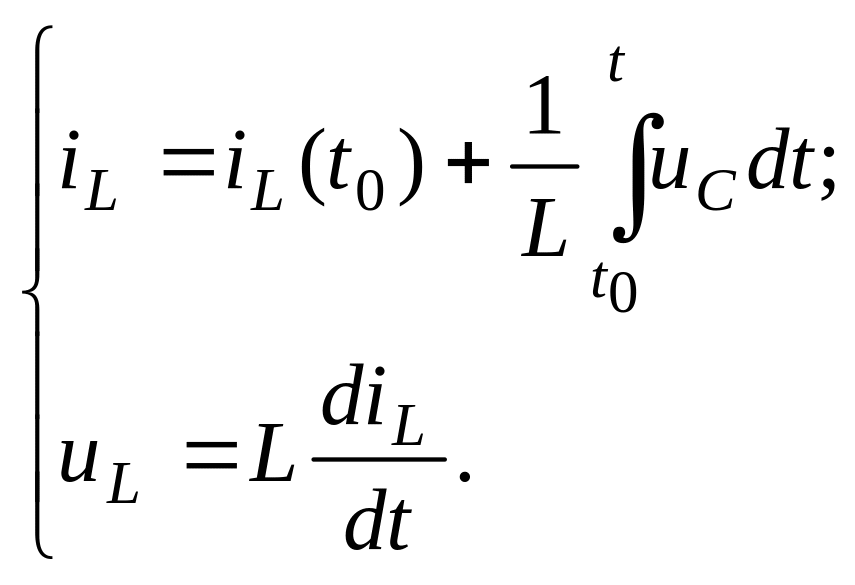1.2)

Классический метод анализа переходных процессов основан на классическом методе решения обыкновенных дифференциальных уравнений. Как известно, общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами a_k вида

(1.3)

относительно независимой переменной v(t) равно сумме двух решений: какого-либо частного решения этого уравнения и общего решения однородного дифференциального уравнения, получаемого из (1.3) при f(t) = 0. Общее решение характеризует так называемые свободные процессы в цепи (обозначим как v_св), т.е. процессы в цепи после коммутации в отсутствие внешних источников энергии. Частное решение дифференциального уравнения определяет принужденный (вынужденный) режим работы цепи (обозначим как v_пр) в новом установившемся режиме после окончания переходного процесса.

Таким образом, искомая реакция цепи v(t) (ток или напряжение какой-либо ветви после коммутации) представляется в виде:

. (1.4)

Для определения принужденной составляющей можно воспользоваться одним из известных методов анализа линейных цепей в установившемся режиме. Очевидно, что если после коммутации токи и напряжения независимых источников энергии не изменяются, то принужденная составляющая реакции цепи является постоянной величиной (постоянный ток или напряжение): v_пр(t) = v_пр = const.

Для определения свободной составляющей реакции цепи необходимо найти корни p_i характеристического уравнения

, (1.5)

где a_n …a₀ – коэффициенты дифференциального уравнения (1.3). Тогда свободная составляющая v_св(t) равна

, (1.6)

где A_i – постоянная интегрирования, определяемая из начальных условий.

Рассмотрим основные этапы анализа переходных процессов в ЭЦ на примере схемы, показанной на рис. 1.1. Для удобства анализа разделим процесс на четыре стадии, сопровождая каждую из них соответствующими эквивалентными схемами (рис. 1.2):

1. установившийся процесс перед коммутацией;

2. быстрое изменение процесса в момент коммутации;

3. медленное изменение процесса после коммутации;

4. установившийся процесс после коммутации (принужденная составляющая переходного процесса).

Этапы анализа переходных процессов

1 . Анализ цепи до коммутации. В результате этого этапа определяют токи индуктивностей и напряжения емкостей в момент времени, непосредственно предшествующий коммутации (t =0_–). Для этого необходимо преобразовать исследуемую схему к виду, соответствующему моменту времени t = 0_– (первая стадия переходного процесса). В цепях постоянного тока из схемы исключаются емкости (разрыв цепи), а индуктивности заменяются идеальным проводником, т.к. в цепях постоянного тока напряжения на конденсаторах постоянны, и токи через них не протекают, а через индуктивности протекают постоянные токи, и падение напряжения на них отсутствует. На схеме (рис. 1.1) коммутатор (S) в исходном состоянии находится в положении «1», и эквивалентная схема приобретает достаточно простой для расчета вид (рис. 1.2, а). Интересующее нас напряжение на емкости С можно найти по правилу делителя напряжений: u_C(0_–) = U_R3 = ER₃/(R₁ + R₃ + R₄).

2 . Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения емкостей в момент времени t = 0₊, которые находят с помощью законов коммутации. Для второй стадии рассматриваемого процесса (момент коммутации) топология ЭЦ соответствует виду «после коммутации». При этом в эквивалентной схеме емкости заменяются идеальными источниками напряжения (E_Ci), а индуктивности – идеальными источниками тока (I_Li) (рис. 1.2, б). Поскольку напряжения емкостей и токи индуктивностей в момент коммутации не изменяются, то E_Ci = u_Ci(0₊) = u_Ci(0_–) и I_Li = i_Li(0₊)= i_Li(0_–). В рассматриваемой схеме начальное (исходное) значение напряжения на конденсаторе С (обозначим как E₁) равно Е₁ = u_C(0₊) = u_C(0_–) = U_R3 = = ER₃/(R₁ + R₃ + R₄) (рис. 1.2, а), а Е_С = Е₁ (рис. 1.2, б).

3. Составление дифференциального уравнения цепи после коммутации. Как отмечалось выше, дифференциальное уравнение цепи получают из системы уравнений энергетического равновесия цепи, составленной любым методом (например, используя законы Кирхгофа), с последующим исключением всех неизвестных величин, кроме одной независимой переменной, представляющей собой ток или напряжение какой-либо ветви. Топология цепи должна соответствовать виду «после коммутации». В ЭЦ первого порядка в качестве независимой переменной, как правило, принимают ток через индуктивность или напряжение на емкости.

Установив в схеме (рис. 1.1) коммутатор (S) в положение «2» и составив для полученной ЭЦ систему уравнений электрического равновесия, с учетом (1.2) получим:

или , (1.7)

где . (1.7, а)

Величина τ = R_эC называется постоянной времени цепи. Для ЭЦ первого порядка, содержащей индуктивность, постоянная времени определяется выражением τ = L/R_э.

Следует отметить, что эквивалентное сопротивление R_э можно найти, используя эквивалентную схему (рис. 1.2, в), которая получается из исходной схемы (после коммутации), если из нее исключить источники постоянного тока, а источники постоянного напряжения заменить идеальным проводником.

Напряжение на емкости при t ≥ 0 представим в виде суммы свободной и принужденной составляющих u_C(t) = u_{C св}(t) + u_{С пр}.

4. Анализ установившегося процесса в цепи после коммутации. Для определения принужденной составляющей реакции ЭЦ необходимо провести анализ установившегося процесса в цепи после коммутации. Для рассматриваемого примера эквивалентная схема в установившемся режиме показана на рис. 1.2, г. Так как напряжение на конденсаторе u_{С пр} = I_R3R₃ и, учитывая, что по правилу делителя тока I_R3 = I∙R₁/(R₁ + + R₂ + R₃), получаем

. (1.8)

Принужденную составляющую можно найти и из выражения (1.7), учитывая, что в установившемся режиме du_C/dt = 0:

. (1.9)

Нетрудно заметить, что выражения (1.8) и (1.9) полностью совпадают.

5. Определение свободной составляющей реакции цепи. Для определения свободной составляющей реакции цепи (1.6) необходимо составить характеристическое уравнение (1.5). Применительно к ЭЦ первого порядка характеристическое уравнение имеет вид τp₁ + 1 = 0, откуда получаем: p₁ = -1/τ. Таким образом, свободная составляющая реакции цепи содержит один экспоненциальный член (в нашем примере свободная составляющая напряжения на емкости):

. (1.10)

6. Нахождение общего вида реакции цепи. Общий вид реакции цепи находится в соответствии с выражением (1.4) и для нашего примера имеет вид

. (1.11)

7. Определение постоянных интегрирования. Для определения постоянной интегрирования A₁ воспользуемся найденным ранее начальным условием u_C(0₊) = Е₁. Полагая в (1.11) t = 0 и u_C = u_C(0₊) = Е₁, получаем E₁ = E₂ + A₁, откуда A₁ = E₁ - E₂.

8. Определение реакции цепи, соответствующей заданным начальным условиям. Искомое напряжение на емкости в ЭЦ (рис. 1.1) после коммутации (t ≥ 0) описывается выражением

, (1.12)

а ток, протекающий через конденсатор, определяется из (1.12):

. (1.13)

Выражения (1.12) и (1.13) для ЭЦ первого порядка, содержащих только постоянные источники энергии, носят универсальный характер. То есть, если цепь содержит индуктивность и в качестве независимой переменной принят ток i_L, то ток и напряжение на индуктивности после коммутации соответственно равны:

, (1.14)

, (1.15)

где I₁ и I₂ – начальное и установившееся значения тока в индуктивности, которые можно найти по эквивалентным схемам установившихся режимов ЭЦ до и после коммутации (рис. 1.2, а и рис. 1.2, г), τ = L/R_э, а R_э – эквивалентное резистивное сопротивление ЭЦ после коммутации.

Г рафики переходного процесса в схеме (рис. 1.1) приведены на рис. 1.3. Для графического определения постоянной времени τ необходимо провести касательную к кривой переходного процесса в любой ее точке. Тогда τ = t₂ – t₁ , где t₁ и t₂ – соответственно абсциссы точки касания и точки пересечения касательной линии установившегося режима.

Определив ток и напряжение на реактивном элементе, можно (используя законы Ома и Кирхгофа) найти токи и напряжения и в других ветвях схемы. Так, в схеме (рис. 1.1) ток, протекающий через сопротивление R₃, равен i₃ = u_C/R₃, а ток, протекающий через R₂, по первому закону Кирхгофа: i₂ = i₃ + i_C и т.д.