
- •I. Выборочный метод. Вариационные ряды. Построение эмпирической функции распределения, гистограммы частот
- •II. Статистические характеристики вариационных рядов. M(X), d(X), σ(X), Mo, Me, показатели вариации. Асимметрия и эксцесс.
- •III. Вычисление групповых и общих средних, групповой, внутригрупповой, межгрупповой дисперсии и общей дисперсии
- •IV. Доверительный интервал и доверительная вероятность (интервальное оценивание)
- •V.Сравнение двух дисперсий нормальных генеральных совокупностей
- •VI. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
VI. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
Пусть
даны две генеральные совокупности (
и
,
из которых извлечены выборки с объемами
и
.
По данным выборкам найдены соответствующие
выборочные средние
,
и исправленные выборочные дисперсии
![]() ,
,
![]() .
Генеральные дисперсии неизвестны, но
предполагаются одинаковыми.
.
Генеральные дисперсии неизвестны, но
предполагаются одинаковыми.
Правило
1. Для
того чтобы при заданном уровне значимости
проверить нулевую гипотезу
![]() о равенстве генеральных средних двух
нормальных совокупностей с неизвестными,
но одинаковыми дисперсиями (в случае
малых независимых выборок) при
конкурирующей гипотезе
о равенстве генеральных средних двух
нормальных совокупностей с неизвестными,
но одинаковыми дисперсиями (в случае
малых независимых выборок) при
конкурирующей гипотезе
![]() ,
надо вычислить наблюдаемое значение
критерия
,
надо вычислить наблюдаемое значение
критерия
 (32)
(32)
и по
таблице критических точек распределения
Стьюдента, по заданному уровню значимости
,
помещенному в верхней строке приложения
2, и числу степеней свободы
![]() найти критическую точку
найти критическую точку
![]() .
Если
.
Если
![]() - нет оснований отвергнуть нулевую
гипотезу. Если
- нет оснований отвергнуть нулевую
гипотезу. Если
![]() - нулевую гипотезу отвергают.
- нулевую гипотезу отвергают.
Правило
2. При
конкурирующей гипотезе
![]() ,
находят критическую точку
,
находят критическую точку
![]() по таблице
приложения2
по заданному
уровню значимости
,
помещенному в нижней строке таблицы, и
числу степеней свободы
найти критическую точку
.
Если
по таблице
приложения2
по заданному
уровню значимости
,
помещенному в нижней строке таблицы, и
числу степеней свободы
найти критическую точку
.
Если
![]() - нет оснований отвергнуть нулевую
гипотезу. Если
- нет оснований отвергнуть нулевую
гипотезу. Если
![]() - нулевую гипотезу отвергают.
- нулевую гипотезу отвергают.
Правило
3. При
конкурирующей гипотезе
![]() ,
находят сначала критическую точку
,
находят сначала критическую точку
![]() по правилу 2 и полагают
по правилу 2 и полагают
![]()
![]() .
Если
.
Если
![]() - нет оснований отвергнуть нулевую
гипотезу. Если
- нулевую гипотезу отвергают.
- нет оснований отвергнуть нулевую
гипотезу. Если
- нулевую гипотезу отвергают.
Таким образом, критическая область строится в зависимости от вида альтернативной (конкурирующей) гипотезы.
Правило построения критических областей и принятия решений можно записать в виде таблицы:
Таблица №16
Нулевая гипотеза |
|
Конкурирующая гипотеза |
а) ; б) ; в) . |
Уровень значимости для критерия |
(часто или ) |
Критерий |
(предполагается, что генеральные дисперсии неизвестны, но равны) |
Критические точки |
Зависят от . а) ; б) ; в) находятся по таблице критических точек распределения Стьюдента. |
Правило принятия решения |
Нулевая гипотеза отклоняется, если: а) ; б) ; в) |
Пример 6. Расход сырья на единицу продукции по старой технологии составил (таблица №17):
Таблица №17
Расходы сырья |
304 |
305 |
306 |
308 |
Число изделий
|
1 |
3 |
2 |
1 |
По новой технологии (таблица №18):
Таблица №18
Расходы сырья
|
303 |
304 |
306 |
308 |
Число изделий
|
2 |
6 |
5 |
2 |
Предположив, что соответствующие генеральные совокупности и имеют нормальное распределение с одинаковыми дисперсиями, проверить при уровне значимости гипотезу при альтернативной гипотезе .
Решение.
Объемы выборок равны
 ,
,
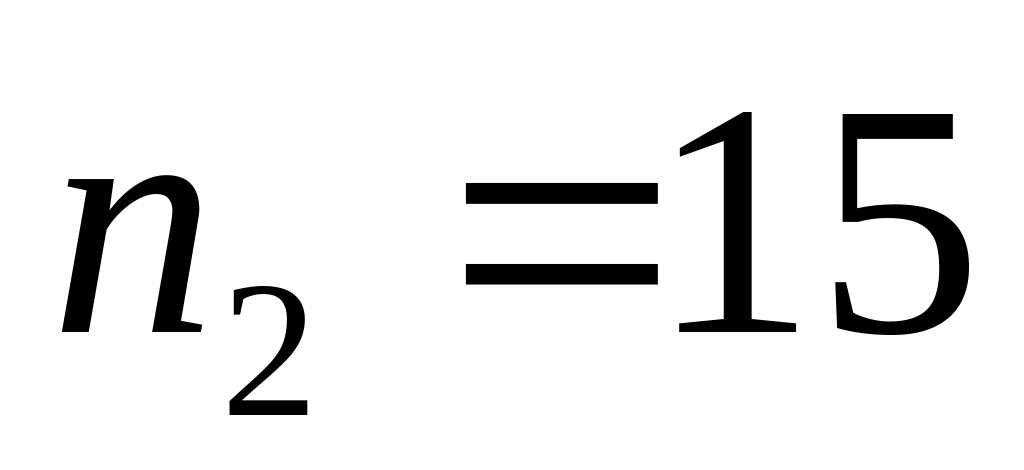 .
.Найдем , :


Найдем выборочные и исправленные дисперсии
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, рассматриваемые дисперсии различны, поэтому надо сравнить дисперсии, используя критерий Фишера – Снедекора. Сделаем это приняв в качестве конкурирующей гипотезы .
Найдем наблюдаемое значение критерия:
 .
С помощью функции
FРАСПОБР(
;
;
)
находим
.
С помощью функции
FРАСПОБР(
;
;
)
находим
 .
Так как
- дисперсии
различаются незначимо и, следовательно
можно считать, что допущение о равенстве
генеральных дисперсий выполняется.
.
Так как
- дисперсии
различаются незначимо и, следовательно
можно считать, что допущение о равенстве
генеральных дисперсий выполняется.Сравним средние, для чего вычислим наблюдаемое значение критерия Стьюдента:
![]()
По условию,
конкурирующая гипотеза имеет вид
,
поэтому критическая область –
двусторонняя. По уровню значимости
и числу степеней свободы
![]() с помощью функции Excel
СТЬЮДРАСПОБР
с помощью функции Excel
СТЬЮДРАСПОБР![]() СТЬЮДРАСПОБР
СТЬЮДРАСПОБР![]() ,т.е.
,т.е.
![]()
![]() .
.
Так как
![]() - нет оснований отвергнуть гипотезу о
равенстве средних. Таким образом при
переходе на новую технологию не происходит
существенного изменения расхода сырья
на одно изделие.
- нет оснований отвергнуть гипотезу о
равенстве средних. Таким образом при
переходе на новую технологию не происходит
существенного изменения расхода сырья
на одно изделие.
Все расчеты можно оформить в виде расчетной таблицы Excel (таблица №19):
Таблица №19
|
|
|
|
|
|
|
|
304 |
1 |
303 |
2 |
43,4286 |
40,4000 |
0,3528 |
0,5695 |
305 |
3 |
304 |
6 |
130,7143 |
121,6000 |
0,1399 |
0,4551 |
306 |
2 |
306 |
5 |
87,4286 |
102,0000 |
0,0525 |
0,2904 |
308 |
1 |
308 |
2 |
44,0000 |
41,0667 |
0,8426 |
1,1473 |
|
7 |
|
15 |
305,5714 |
305,0667 |
1,3878 |
2,4622 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9830 |
2,6381 |
|
|
|
|
FРАСПОБР(0,05;14;7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СТЬЮДРАСПОБР |
|
|
|
Задача 6.
Из двух партий изделий, изготовленных
на двух одинаково настроенных станках,
извлечены малые выборки (![]() ;
;![]() ).
Требуется при уровне значимости
проверить гипотезу
).
Требуется при уровне значимости
проверить гипотезу
![]() о равенстве
средних размеров изделий при конкурирующей
гипотезе
о равенстве
средних размеров изделий при конкурирующей
гипотезе
![]() .
Предполагается,
что случайные величины
и
распределены нормально.
.
Предполагается,
что случайные величины
и
распределены нормально.
Все расчеты оформить в виде расчетной таблицы Excel
ПРИЛОЖЕНИЯ
Приложение 1
Значения
![]()
|
0,95 |
0,99 |
0,999 |
5 |
2,78 |
4,60 |
8,61 |
6 |
2,57 |
4,03 |
6,86 |
7 |
2,45 |
3,71 |
5,96 |
8 |
2,37 |
3,50 |
5,41 |
9 |
2,31 |
3,36 |
5,04 |
10 |
2,26 |
3,25 |
4,78 |
11 |
2,23 |
3,17 |
4,59 |
12 |
2,20 |
3,11 |
4,44 |
13 |
2,18 |
3,06 |
3,32 |
14 |
2,16 |
3,01 |
4,22 |
15 |
2,15 |
2,98 |
4,14 |
16 |
2,13 |
2,95 |
4,07 |
17 |
2,12 |
2,92 |
4,02 |
18 |
2,11 |
2,90 |
3,97 |
19 |
2,10 |
2,88 |
3,92 |
20 |
2,093 |
2,86 |
3,883 |
25 |
2,064 |
2,797 |
3,745 |
30 |
2,045 |
2,756 |
3,659 |
35 |
2,032 |
2,720 |
3,600 |
40 |
2,023 |
2,709 |
3,558 |
45 |
2,016 |
2,092 |
3,527 |
50 |
2,009 |
2,679 |
3,502 |
60 |
2,001 |
2,662 |
3,464 |
70 |
1,996 |
2,649 |
3,439 |
80 |
1,991 |
2,640 |
3,418 |
90 |
1,987 |
2,623 |
3,403 |
100 |
1,984 |
2,627 |
3,392 |
120 |
1,980 |
2,617 |
3,374 |
|
1,960 |
2,576 |
3,291 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов: М.: Высш. шк., 2001. - 479с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учеб. пособие для вузов: М.: Высш. шк., 2001. - 400с.
Калинина В.Н., Панкин В.Ф.Математическая статистика: Учебник для студентов сред. спец. учеб. заведений: М.: Высш. шк., 2001. - 336с.
Ниворожкина Л.И., Морозова З.А. Математическая статистика с элементами теории вероятностей в задачах с решениями: Учебное пособие. – Москва: ИКЦ «МарТ»; Ростов-н/Д: Издательский центр «МарТ», 2005.- 608с.
Законы распределения и предельные теоремы. Элементы математической статистики: Методические указания и тренировочные тесты к курсу «Теория вероятностей и математическая статистика для студентов вечернего отделения»/Сост. В.И. Киршбаум, А.Ю. Смыслов. Самара: СПтИ, 1991. 43с.


