
- •I. Выборочный метод. Вариационные ряды. Построение эмпирической функции распределения, гистограммы частот
- •II. Статистические характеристики вариационных рядов. M(X), d(X), σ(X), Mo, Me, показатели вариации. Асимметрия и эксцесс.
- •III. Вычисление групповых и общих средних, групповой, внутригрупповой, межгрупповой дисперсии и общей дисперсии
- •IV. Доверительный интервал и доверительная вероятность (интервальное оценивание)
- •V.Сравнение двух дисперсий нормальных генеральных совокупностей
- •VI. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
V.Сравнение двух дисперсий нормальных генеральных совокупностей
Рассмотрим
две генеральные совокупности (![]() и
и
![]() ,
распределенные нормально. Из них
извлекаются две независимые случайные
выборки с объемами
,
распределенные нормально. Из них
извлекаются две независимые случайные
выборки с объемами
![]() и
.
Для каждой выборки найдены исправленные
выборочные дисперсии:
и
.
Для каждой выборки найдены исправленные
выборочные дисперсии:
![]() (28)
(28)
![]() (29)
(29)
Требуется
сравнить эти дисперсии, т.е. проверить
нулевую гипотезу
![]() .
В качестве проверки этой гипотезы
применяется статистика (наблюдаемое
значение критерия):
.
В качестве проверки этой гипотезы
применяется статистика (наблюдаемое
значение критерия):
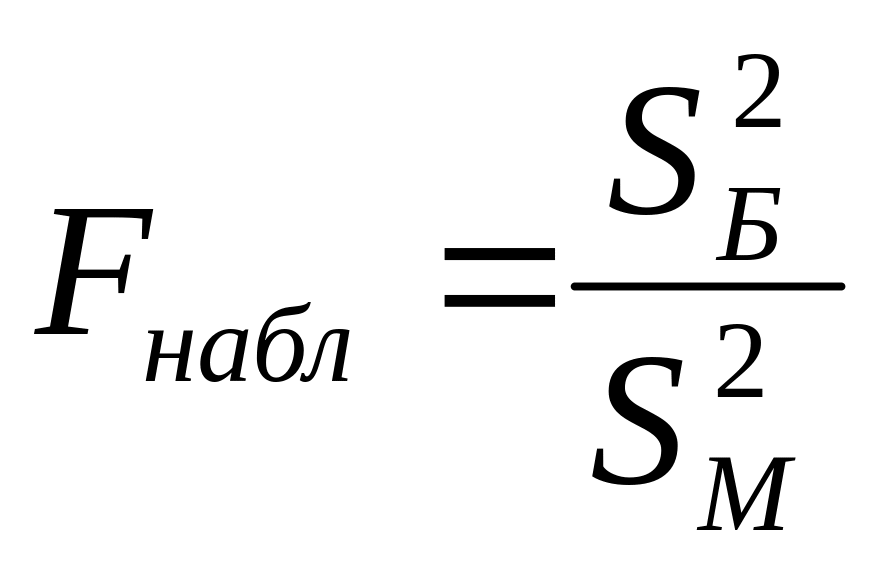 (
(![]() ), (30)
), (30)
которая
при условии справедливости нулевой
гипотезы имеет распределение
Фишера-Снедекора со степенями свободы
![]() и
и
![]() .
.
Правило
1. Для
того чтобы при заданном уровне значимости
![]() проверить нулевую гипотезу
проверить нулевую гипотезу
![]() о равенстве генеральных дисперсий
нормальных совокупностей при конкурирующей
гипотезе
о равенстве генеральных дисперсий
нормальных совокупностей при конкурирующей
гипотезе
![]() ,
надо вычислить наблюдаемое значение
критерия по формуле (24) (отношение большей
исправленной дисперсии к меньшей) и по
таблице критических точек распределения
Фишера-Снедекора, по заданному уровню
значимости
и числам степеней свободы
,
(
,
надо вычислить наблюдаемое значение
критерия по формуле (24) (отношение большей
исправленной дисперсии к меньшей) и по
таблице критических точек распределения
Фишера-Снедекора, по заданному уровню
значимости
и числам степеней свободы
,
(![]() - число степеней свободы большей
исправленной дисперсии) найти критическую
точку
- число степеней свободы большей
исправленной дисперсии) найти критическую
точку
![]() .
Если
.
Если
![]() - нет
оснований отвергнуть нулевую гипотезу.
Если
- нет
оснований отвергнуть нулевую гипотезу.
Если
![]() - нулевую
гипотезу отвергают.
- нулевую
гипотезу отвергают.
Правило
2. При
конкурирующей гипотезе
![]() критическую точку
критическую точку
![]() ищут по уровню значимости
ищут по уровню значимости
![]() (вдвое меньшему заданного) и числам
степеней свободы
и
(вдвое меньшему заданного) и числам
степеней свободы
и
![]() (
- число степеней свободы большей
исправленной дисперсии). Если
- нет
оснований отвергнуть нулевую гипотезу.
Если
- нулевую
гипотезу отвергают.
(
- число степеней свободы большей
исправленной дисперсии). Если
- нет
оснований отвергнуть нулевую гипотезу.
Если
- нулевую
гипотезу отвергают.
Алгоритм построения критических областей можно записать в виде таблицы №12:
Таблица №12
Нулевая гипотеза |
|
Конкурирующая гипотеза |
а) ; б) |
Уровень значимости для критерия |
(часто
|
Критерий |
( ) |
Критические точки |
Зависят от . а) ; б) ; находятся по таблице критических точек Фишера-Снедекора. |
Правило принятия решения |
Нулевая гипотеза
а)
б)
|
Пример
5. Для сравнения
точности двух станков-автоматов взяты
две пробы (выборки), объемы которых
![]() и
и
![]() .
В результате измерения контролируемого
размера отобранных изделий получены
следующие результаты:
.
В результате измерения контролируемого
размера отобранных изделий получены
следующие результаты:
Таблица №13
|
1,08 |
1,10 |
1,12 |
1,14 |
1,15 |
1,25 |
1,36 |
1,38 |
1,40 |
1,42 |
|
1,11 |
1,12 |
1,18 |
1,22 |
1,33 |
1,35 |
1,36 |
1,38 |
|
|
Можно
ли считать, что станки обладают одинаковой
точностью (
),
если принять уровень значимости
![]() и в качестве конкурирующей гипотезы
.
и в качестве конкурирующей гипотезы
.
Решение.
Найдем выборочные средние
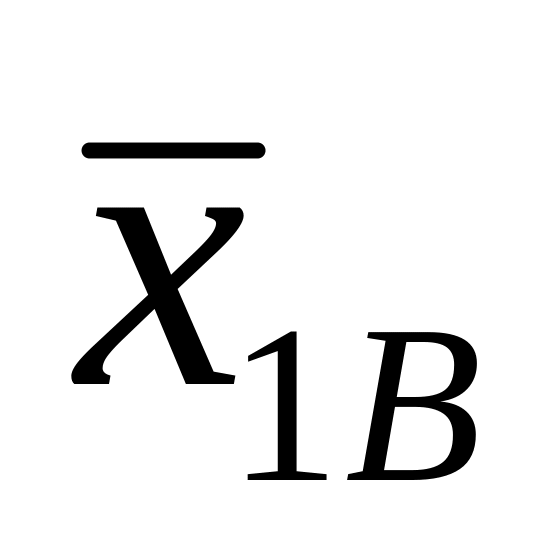 и
и
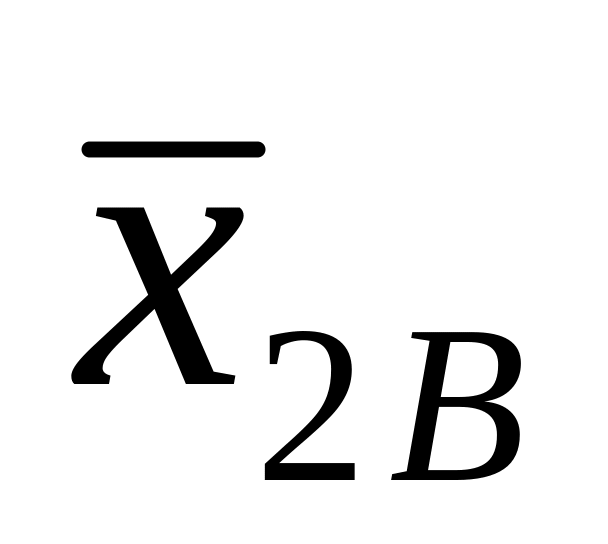 по формуле:
по формуле:
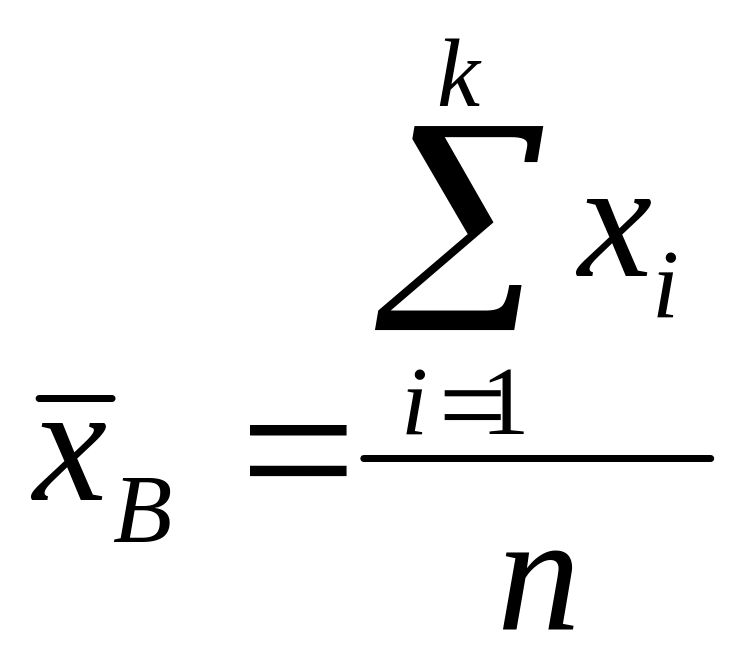 (31)
(31)
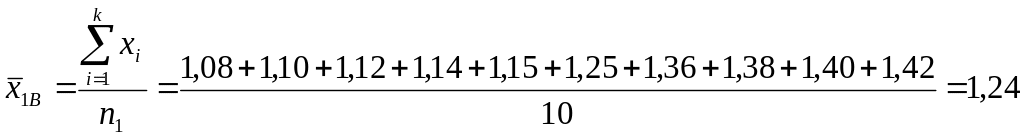
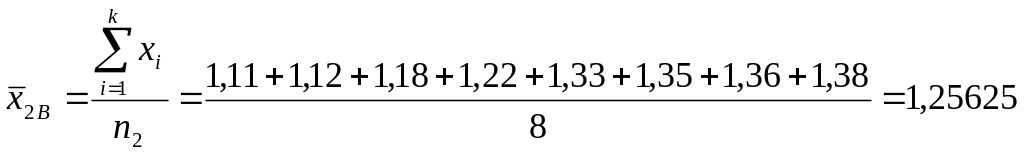 .
.
Вычислим исправленные дисперсии по формулам (28), (29):
![]()
![]() ;
;
![]() ;
;
![]()
![]()
![]() .
.
Найдем , т.е. отношение большей исправленной дисперсии к меньшей:
![]() ;
;
![]() ;
;
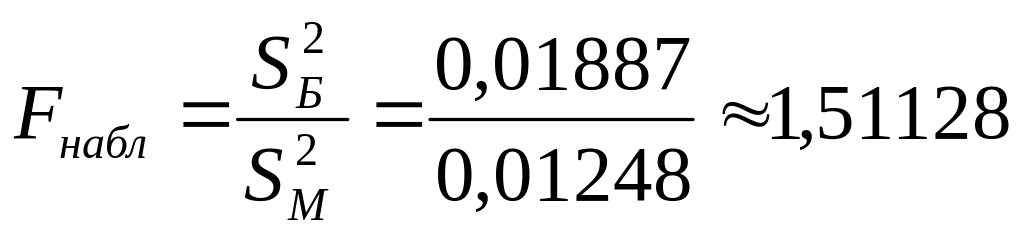 .
.
По таблице или с помощью встроенной функции Excel (статистические) FРАСПОБР( ; ; ), по уровню значимости
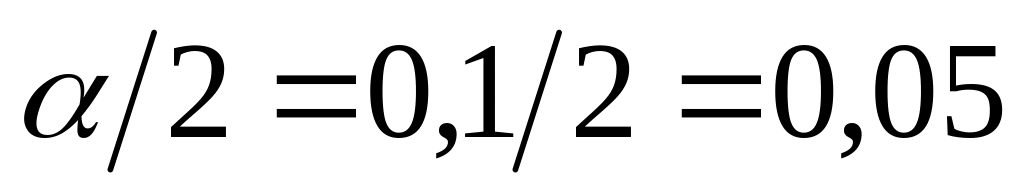 и числам степеней свободы
и числам степеней свободы
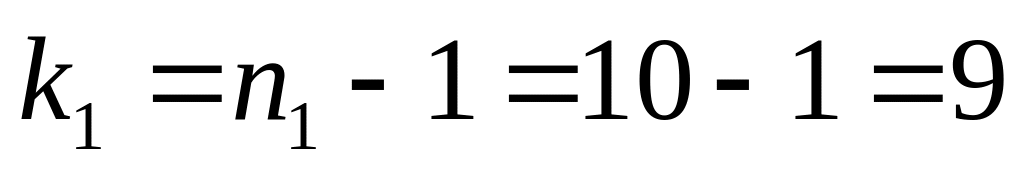 и
и
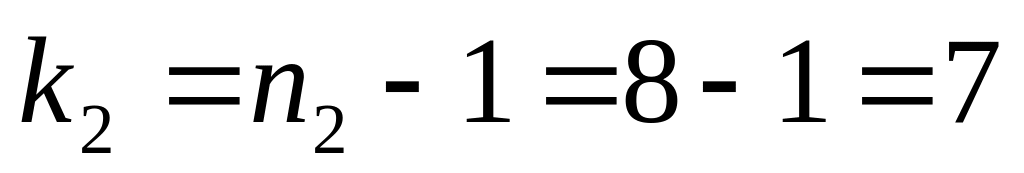 находим критическую точку
находим критическую точку
![]() .
.
Так как - нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий.
Расчетная таблица:
Таблица №14
|
|
|
|
1,08 |
1,11 |
0,00256 |
0,00267 |
1,10 |
1,12 |
0,00196 |
0,00232 |
1,12 |
1,18 |
0,00144 |
0,00073 |
1,14 |
1,22 |
0,00100 |
0,00016 |
1,15 |
1,33 |
0,00081 |
0,00068 |
1,25 |
1,35 |
0,00001 |
0,00110 |
1,36 |
1,36 |
0,00144 |
0,00135 |
1,38 |
1,38 |
0,00196 |
0,00191 |
1,40 |
|
0,00256 |
|
1,42 |
|
0,00324 |
|
12,40 |
10,05 |
0,01698 |
0,01092 |
|
|
|
|
1,24 |
1,25625 |
0,01887 |
0,01248 |
|
|
|
|
|
10 |
|
1,51128 |
|
8 |
|
3,67667 |
Задача
5. Двумя
методами проведены измерения одной и
той же физической величины. Получены
следующие данные
и
![]() .
Можно ли считать, что оба метода
обеспечивают одинаковую точность
измерений, если принять уровень значимости
.
Можно ли считать, что оба метода
обеспечивают одинаковую точность
измерений, если принять уровень значимости
![]() ?
?
Таблица №15
|
|
10,2 |
9,8 |
15,2 |
15,1 |
20,2 |
19,9 |
25,2 |
24,9 |
30,2 |
29,7 |
35,2 |
35,7 |
40,2 |
39,9 |
|
23,9 |
