IV. Доверительный интервал и доверительная вероятность (интервальное оценивание)
Пусть
- оценка некоторой числовой характеристики
генеральной совокупности. Интервал
,
в который с заданной вероятностью
попадает величина
,
называется доверительным
интервалом
(рис.1).
Рис.1
Число
является характеристикой точности
оценки и определяется из равенства
(26)
Число называется доверительной вероятностью, обычно оно задается равным 0,95; 0,99; 0,999. Требуется найти точность и доверительный интервал.
В частности, если
известно среднее квадратическое
отклонение (
)
генеральной совокупности, то доверительный
интервал для оценки математического
ожидания
случайной величины
,
распределенной по нормальному закону,
определяется неравенствами:
, (27)
Здесь
- выборочное среднее,
- это значение аргумента, при котором
функция Лапласа (
)
имеет значение
.
Если
неизвестно, то доверительный интервал
определяется также из условий (27), но
значения
находят по таблице приложения 1, а
полагают равным выборочному среднему
квадратическому отклонению (
).
При
значения
найденные по таблице приложения 1 и по
формуле
совпадают. Если
достаточно велико, то условие нормальности
распределения не требуется.
Пример 4. С целью определения средней суммы вкладов в коммерческом банке, произведено выборочное обследование 500 вкладчиков, которое дало следующие результаты:
Таблица №10
Сумма вклада, тыс.руб. |
10-30 |
30-50 |
50-70 |
70-90 |
90-110 |
110-130 |
Число вкладов |
30 |
40 |
100 |
200 |
60 |
70 |
Пользуясь этими данными, найти доверительные границы для генеральной средней, которые можно было бы гарантировать с вероятностью 0,95.
Решение.
Найдем значения - представителей интервалов по формуле , где - начало интервала, - конец интервала.
;
;
;
;
;
.
Найдем по формуле (2):
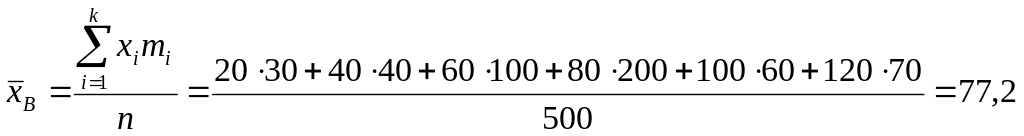
Вычислим выборочную дисперсию (формула (3)) и выборочное среднее квадратическое отклонение (формула (4)), т.к. при больших
:
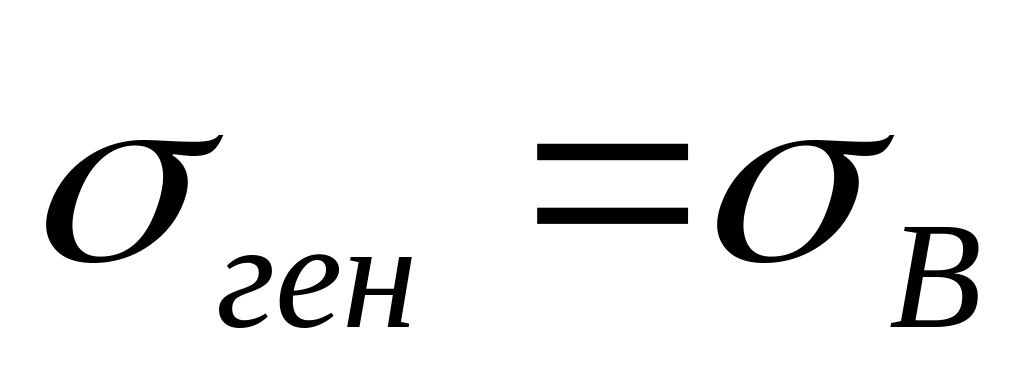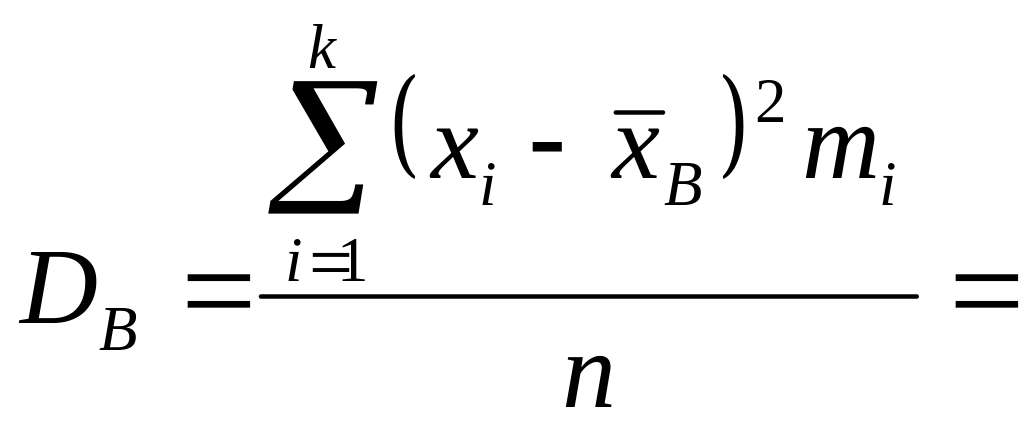
Вычислим значение по таблице значений функции Лапласа.
Т.к.
по условию доверительная вероятность
,
то
,
.
Найдем доверительный интервал для оценки генеральной средней (математического ожидания) по формуле (21):
;
.
Все расчеты легко выполнить в табличном процессоре Excel и оформить в виде расчетной таблицы:
Сумма вклада, (тыс. руб.) |
Число вкладов .( ) |
|
|
|
10 |
|
|
|
|
30 |
30 |
20 |
1,2 |
196,3104 |
50 |
40 |
40 |
3,2 |
110,7072 |
70 |
100 |
60 |
12,0 |
59,1680 |
90 |
200 |
80 |
32,0 |
3,1360 |
110 |
60 |
100 |
12,0 |
62,3808 |
130 |
70 |
120 |
16,8 |
256,4576 |
|
500 |
|
77,2 |
688,1600 |
|
|
|
|
|
|
26,2328 |
Доверительный интервал |
||
|
0,475 |
|||
|
1,96 |
|
74,90059336 |
79,49940664 |
Задача 4. С целью определения средней суммы вкладов в сберегательной кассе, произведено выборочное обследование (бесповторный отбор) 111 вкладчиков, которое дало следующие результаты:
Таблица № 11
Сумма вклада, тыс.руб. |
10-30 |
30-50 |
50-70 |
70-90 |
90-110 |
110-130 |
Число вкладов |
1 |
3 |
10 |
30 |
60 |
7 |
Пользуясь этими данными найти доверительные границы для генеральной средней, которые можно было бы гарантировать с вероятностью 0,99.