5 Асимптоты графика функции

У графика функции различают вертикальные и наклонные асимптоты

Определение Если в точке функция препертивает бесконечный разрыв, т.е. точка разрыва второго рода, то прямая назывется вертикальной асимптотой графика функции

Замечание Вертикальные асимптоты графика функции указываются по результатам исследования в п.4.

Различают правосторонние вертикальные асимптоты, если , а и левосторонние вертикальные асимптоты, если , а .

Определение Прямая называется асимптотой графика функции , если расстояние от точки графика функции до этой прямой стремится к нулю при бесконечном удалении точки М по кривой от начала координат

Замечание График функции может пересекать свою асимптоту, важно что при расстояние точки М(x,y) графика функции от асимптоты стремится к нулю (рис.1)

Рис.1

Определение Прямая называется наклонной асимптотой графика функции , если существуют пределы:

При этом указанные пределы могут быть различными при (для правой наклонной асимптоты) и при (для левой наклонной асимптоты).

Замечание 5 Если k = 0 и существуют пределы:

или ,

То прямая называется горизонтальной асимптотой графика функции

Найти асимптоты графиков функций

5.1

Так как в точках функция претерпевает бесконечный разрыв, то график функции имеет вертикальные асимптоты : (рис.2)

Для отыскания наклонной асимптоты найдем следующие пределы:

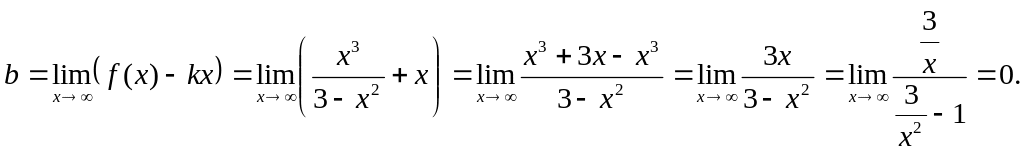
Таким образом, существует наклонная асимптота (рис.2)

у

0 х

Рис.2

5.2

 Так как функция не имеет бесконечных разрывов, то вертикальных асимптот нет. Функция определена в интервале , поэтому для отыскания наклонных асимптот, рассматривается предел только при .

Находим: .

Так как , то делаем вывод, что наклонных асимптот нет

5.3

 Так как в точках функция претерпевает бесконечный разрыв, то график функции имеет вертикальные асимптоты : .

Значения функции в точке рассматриваются только слева, то прямая называется левая вертикальная асимптота, в точке только справа , то прямая – правая вертикальная асимптота.

Для отыскания наклонной асимптоты найдем следующие пределы:

/

.

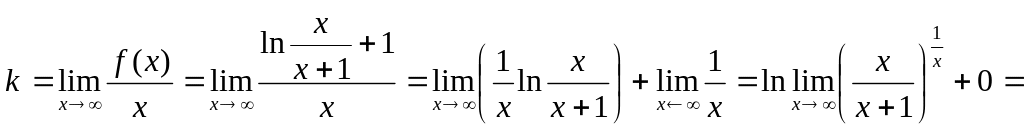
Таким образом, имеется асимптота – горизонтальная асимптота

5.4 Составить уравнения асимптот графика функции .Схематично построить чертеж

 1 Найдем :

. По аналитическому заданию функции можно определить, что , т.е. график функции проходит только над осью ОХ.

Так как , то прямая – правая вертикальная асимптота.

Определим, существуют ли наклонные асимптоты?

Находим:

.

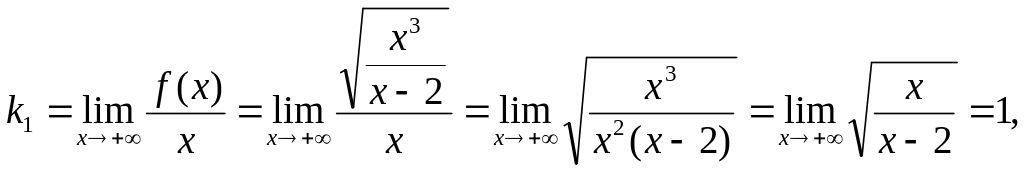
Таким образом существует правая наклонная асимптота ;

(выполните вычисления предела самостоятельно).

Итак, существует левая наклонная асимптота (рис. 3)

Рис. 3

Выполните самостоятельно

Найдите асимптоты графиков функций

5.5 . Ответ: .

5.6 . Ответ: .

5.7 . Ответ: .

5.8 . Ответ: