Исследование температурной зависимости электросопротивления 47

Лабораторная работа № 5 Исследование температурной зависимости электрического сопротивления металлов и полупроводников

Цель работы: ознакомление с классическим методом измерения сопротивления при помощи резистивного моста; вычисление удельного сопротивления, температурного коэффициента сопротивления металла; определение энергии активации примесей в полупроводнике.

Оборудование: мост постоянного тока, нагреватель, измеритель температуры, медный провод, полупроводник.

Краткие теоретические сведения

1. Закон Ома

В 1826 г. немецкий физик Георг Симон Ом экспериментально установил закон, согласно которому сила тока I, протекающего по однородному проводнику, пропорциональна напряжению U на его концах:

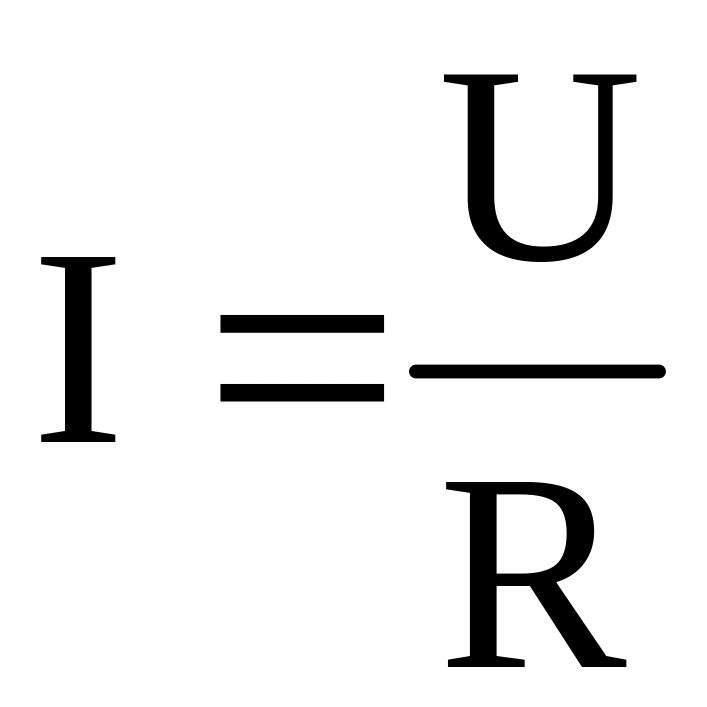, (5.1)

где R  электрическое сопротивление проводника.

Это соотношение не является универсальным законом, так как электрическое сопротивление R не является константой материала. Оно зависит от формы и размеров электрического проводника. Однако можно выделить в сопротивлении R константу материала  удельное сопротивление .

Наиболее просто это сделать для проводников правильной формы. Так, для однородного проводника цилиндрической формы сопротивление R выражается через удельное сопротивление  следующим образом:

, (5.2)

где  длина проводника; S  площадь его поперечного сечения.

Чтобы понять, какие физические величины определяют удельное сопротивление, его необходимо выразить через другие константы материала,

как это делается в классической электронной теории (КЭТ).

2. Вывод закона Ома на основе кэт

КЭТ металлов основана на следующих представлениях. Атом можно представлять как совокупность двух систем электронов. Одна из систем сильно связана с ядром и образует так называемый остов. Другая система, система валентных электронов, у некоторых атомов, например, у атомов щелочных элементов, слабо связана с ядром. При объединении таких атомов в твердое тело, каждый остов занимает вполне определенное место - узел, а совокупность узлов образует кристаллическую решетку. Валентные электроны уже не принадлежат тому или иному остову, а образуют "электронный газ", газ свободных электронов, принадлежащий всему твердому телу в целом. Электронному газу приписываются свойства идеального одноатомного газа. Свободные электроны непрерывно хаотически движутся, причем средняя кинетическая энергия их движения

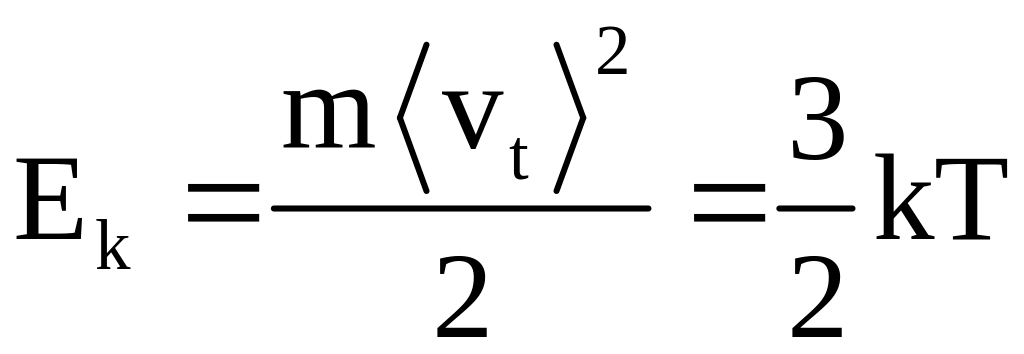, (5.3)

где m  масса электрона;  средняя скорость теплового движения; k- постоянная Больцмана; T  термодинамическая температура.

Под действием внешнего электрического поля свободные электроны приобретают дополнительную скорость, направленную противоположно направлению поля. Это медленное (по сравнению с тепловым движением) направленное движение электронов называется дрейфом, а дополнительная скорость – скоростью дрейфа , или дрейфовой скоростью. Максимальная величина дрейфовой скорости определяется частотой соударений электронов с тем или иным остовом. Каждый остов совершает колебательные движения, амплитуда колебаний определяется температурой твердого тела. При повышении температуры возрастает амплитуда колебаний ионов и, следовательно, увеличивается вероятность столкновения электронов с ионами. В результате скорость дрейфа электронов уменьшается, соответственно уменьшается и ток I. При неизменной разности потенциалов на концах проводника уменьшение тока означает по закону Ома (5.1) рост сопротивления проводника R. С уменьшением же температуры остовы колеблются все менее интенсивно, все реже соударения электронов с ионами. Поэтому сопротивление проводника убывает с уменьшением температуры.

На основе этих представлений КЭТ найдем связь удельного сопротивления с другими константами материала.

В промежутке между двумя следующими друг за другом соударениями электроны под действием кулоновской силы F = eE двигаются с ускорением

, (5.4)

где e  заряд; m масса электрона; E  напряженность электрического поля.

Скорость дрейфа и время между двумя последующими соударениями являются случайными величинами. Можно предполагать, что эти величины распределены в интервале от нуля до некоторых максимальных значений. Если  среднее время между двумя последующими соударениями, или среднее время свободного пробега электронов, то максимальная дрейфовая скорость, которую электрон приобретает перед соударением, равна

. (5.5)

Средняя скорость дрейфа электронов равна, очевидно, половине максимальной, так как сразу же после соударения скорость дрейфа равна нулю, а затем растет со временем линейно. Используя это соображение и заменяя в (5.5) ускорение его значением из (5.4), получим:

. (5.6)

Здесь величина

(5.7)

называется подвижностью электронов, имеет размерность м²/В с и численно равна средней дрейфовой скорости в единичном поле.

Для однородного проводника цилиндрической формы с площадью поперечного сечения S силу тока I можно выразить через скорость дрейфа . За время t электроны проходят вдоль проводника расстояние . Пусть в единице объема имеется n электронов проводимости. Число электронов, пересекающих сечение S проводника за время t, составляет nSL. Заряд Q, проходящий через это сечение, равен . Так как сила тока I равна Q/t, тогда

, (5.8)

где n  концентрация электронов.

Подставляя в (5.8) значение дрейфовой скорости из (5.6) и учитывая, что , где  длина проводника, получим

. (5.9)

Из сравнения полученного выражения с законом Ома (5.1) получим, что

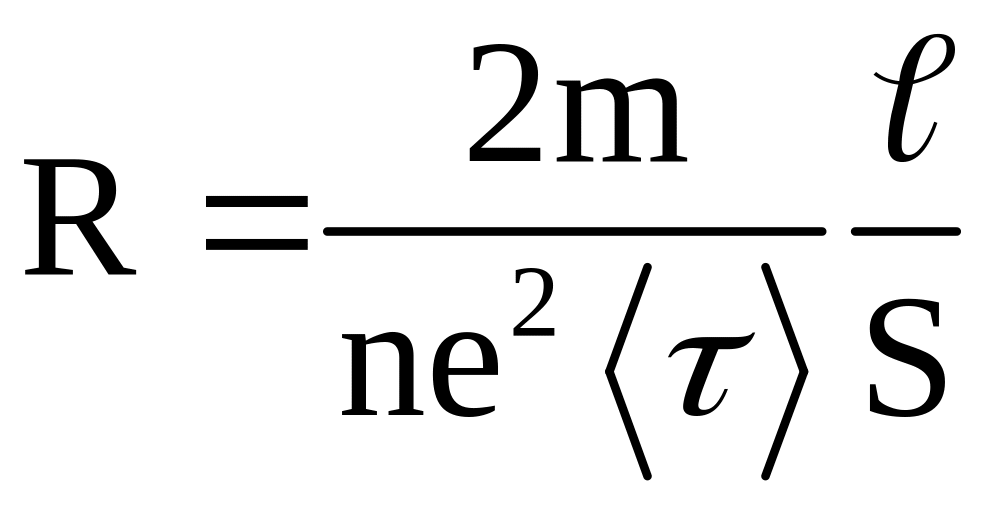. (5.10)

Сопоставляя выражения (5.10) и (5.2), можно легко получить искомую связь материальной константы  с фундаментальными константами (заряд и масса электрона) и другими материальными константами (концентрация и среднее время свободного пробега электронов):

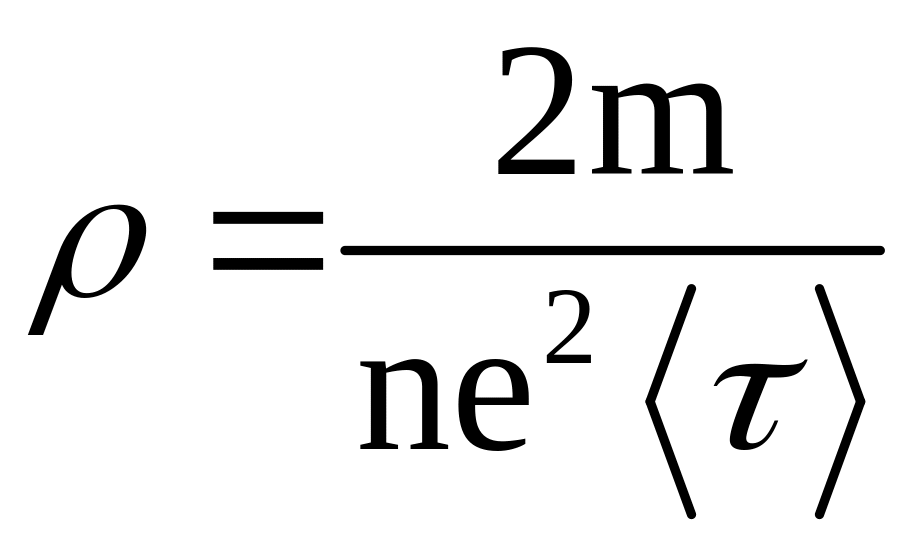. (5.11)