
- •Список литературы
- •Список литературы
- •Колебательной системы
- •Активной массы от соотношения частот при различных величинах затухания в горизонтальном направлении системы
- •Активной массы от соотношения частот при различных величинах затухания в вертикальном направлении системы
- •Список литературы
- •Параметры маятниковой схемы стенда
- •Список литературы
- •Список литературы
- •Дискового зубчатого бункерного загрузочного устройства с кольцевым ориентатором
- •С неярко выраженной асимметрией торцов и смещения центра масс вдоль продольной оси симметрии на дне бункера бзу
- •Захватывающих органов дискового зубчатого бункерного загрузочного устройства
Колебательной системы
На рис. 2 обозначены:
1.
![]() – соответственно жесткости амортизаторов
12, 13 (см. рис. 1) и упругой системы
горизонтального привода. Коэффициенты
неупругого сопротивления амортизаторов
и упругой системы между активной и
реактивной части системы горизонтального
привод -
– соответственно жесткости амортизаторов
12, 13 (см. рис. 1) и упругой системы
горизонтального привода. Коэффициенты
неупругого сопротивления амортизаторов
и упругой системы между активной и
реактивной части системы горизонтального
привод -
![]() .
.
2.
![]() – соответственно, жесткости амортизаторов
12, 13 (см. рис. 1) и упругой системы между
активной и реактивной частями
вертикального привода. Коэффициенты
неупругого сопротивления амортизаторов
и упругой системы между активной и
реактивной частями системы вертикального
привода -
– соответственно, жесткости амортизаторов
12, 13 (см. рис. 1) и упругой системы между
активной и реактивной частями
вертикального привода. Коэффициенты
неупругого сопротивления амортизаторов
и упругой системы между активной и
реактивной частями системы вертикального
привода -
![]() .
.
3.
![]() – амплитуды возмущающего момента
горизонтальных колебаний и силы
вертикальных колебаний, соответственно.
– амплитуды возмущающего момента
горизонтальных колебаний и силы
вертикальных колебаний, соответственно.
Принимая для
системы горизонтальных колебаний в
качестве обобщенных координат
![]() и
угловые перемещения инерционных
элементов
и
угловые перемещения инерционных
элементов
![]() и
и
![]() ,
записывая выражения кинетической и
потенциальной энергии, а также функции
диссипации, дифференцируя их, и подставляя
в уравнение Лагранжа 2-го рода, получим
следующие дифференциальные уравнения
движения систем
,
записывая выражения кинетической и
потенциальной энергии, а также функции
диссипации, дифференцируя их, и подставляя
в уравнение Лагранжа 2-го рода, получим
следующие дифференциальные уравнения
движения систем
![]() (1)
(1)
где
![]() – угловая
частота возбуждения колебаний.
– угловая
частота возбуждения колебаний.
При наличии в линейных дифференциальных уравнениях членов с четными и нечетными производными решения следует искать через синусоидальные и косинусоидальные компоненты, иными словами, с двумя неизвестными компонентами (или через амплитудную величину и фазу перемещения)
![]() (2)
(2)
Получим систему алгебраических уравнений, из которой согласно [1] определитель системы раскрывается как сумма квадратов действительной и мнимой частей
![]() (3)
(3)
![]() (4)
(4)
Величины амплитуд колебаний масс и фазовых сдвигов по отношению к возмущающему моменту в соответствии с работой [1] определяются по следующим формулам:
![]() (5)
(5)
![]()
 (6)
(6)
![]()
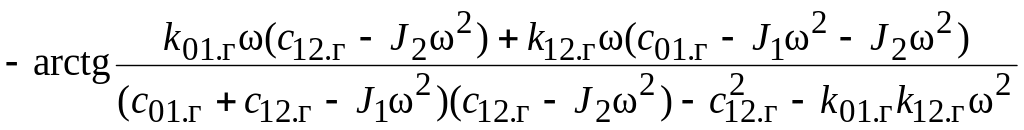 .
(7)
.
(7)
Из (4) мы разделим
![]() ,
,![]() на
на
![]() и обозначив
и обозначив
![]()
![]()
![]() ;
;
![]() (8)
(8)
Имеем
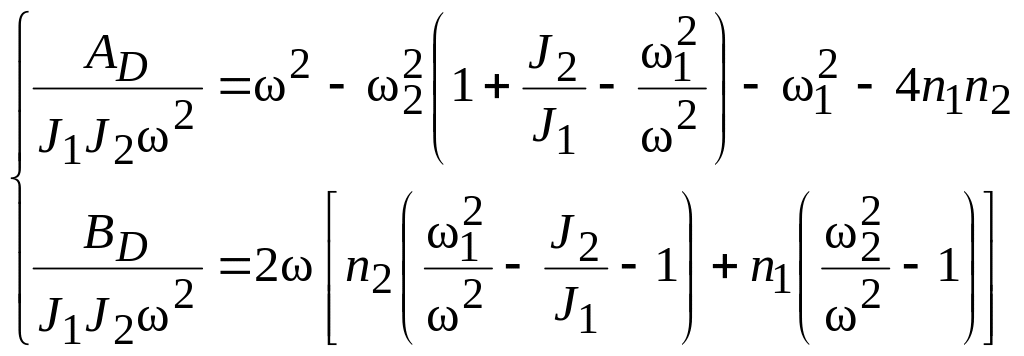
Пренебрегая
вследствие малости произведением
![]() и обозначая
и обозначая
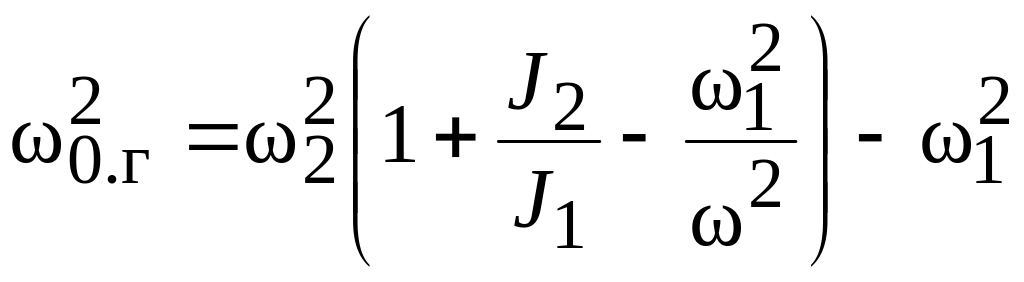 ;
;
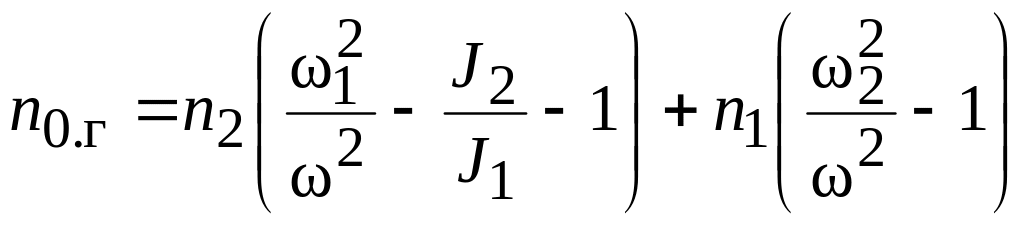 (9)
(9)
имеем
![]() (10)
(10)
Из (10), (5), (6), (7) перепишем
 (11)
(11)
 (12)
(12)
Используя (11), (12) и задавая примерные параметры системы строим графики зависимостей амплитуды и угла сдвига фаз активной массы от соотношения частот на рис. 3.
Аналогично, для вертикальных колебаний, применяя тот же метод [1] получаем выражения амплитуд
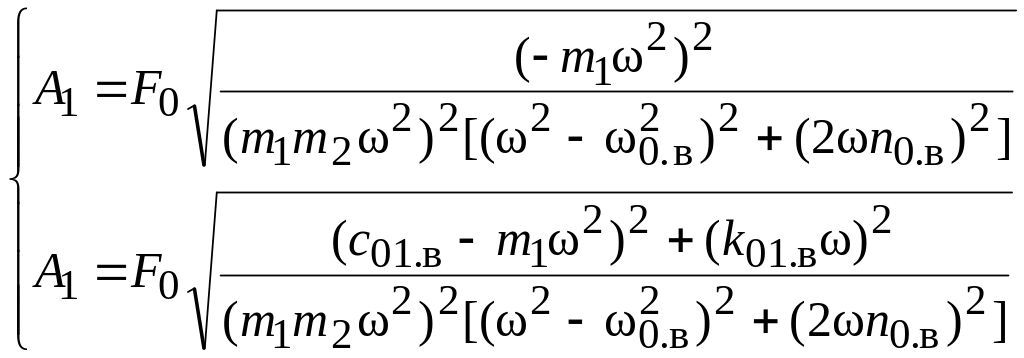
![]() (13)
(13)
и угла сдвига фаз
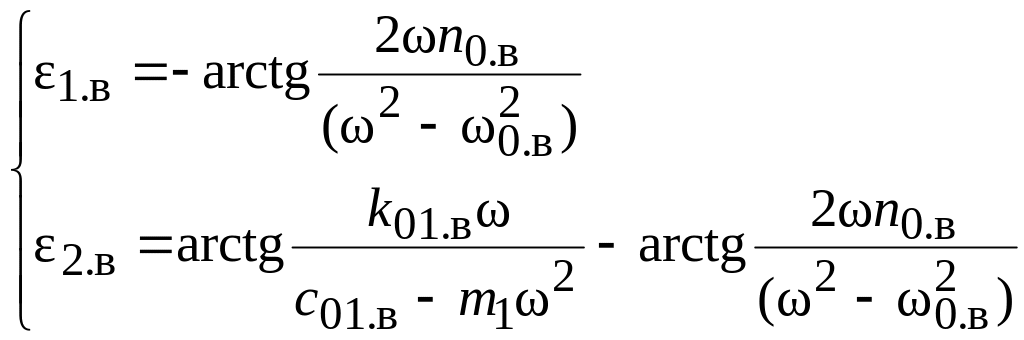 (14)
(14)
Мы считаем жесткость механической конструкции (рычаги 10, 14; вал 11, см. рис. 1) бесконечной, поэтому вертикальная суммарная жест-
кость
![]()
где с9 - жесткость центральной пружины 9.
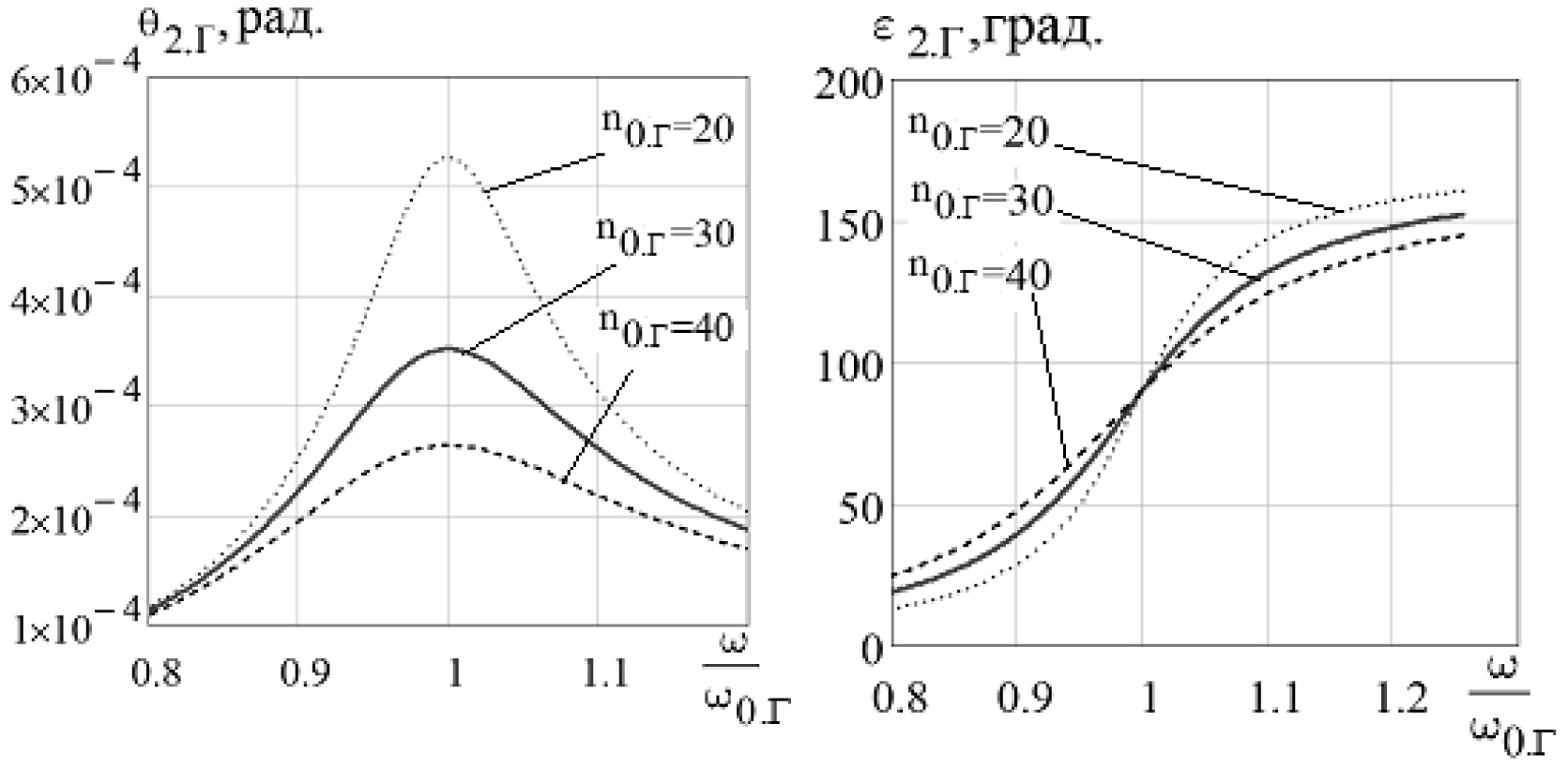
а б
Рис. 3. Графики зависимости амплитуды (а) и угла сдвига фаз (б)
Активной массы от соотношения частот при различных величинах затухания в горизонтальном направлении системы
![]()
![]()
![]() ;
;
![]()

Используя (13) и (14) и также задавая примерные параметры системы строим графики, выражающие зависимость амплитуды и угла сдвига фаз активной массы от соотношения частот (рис. 4).
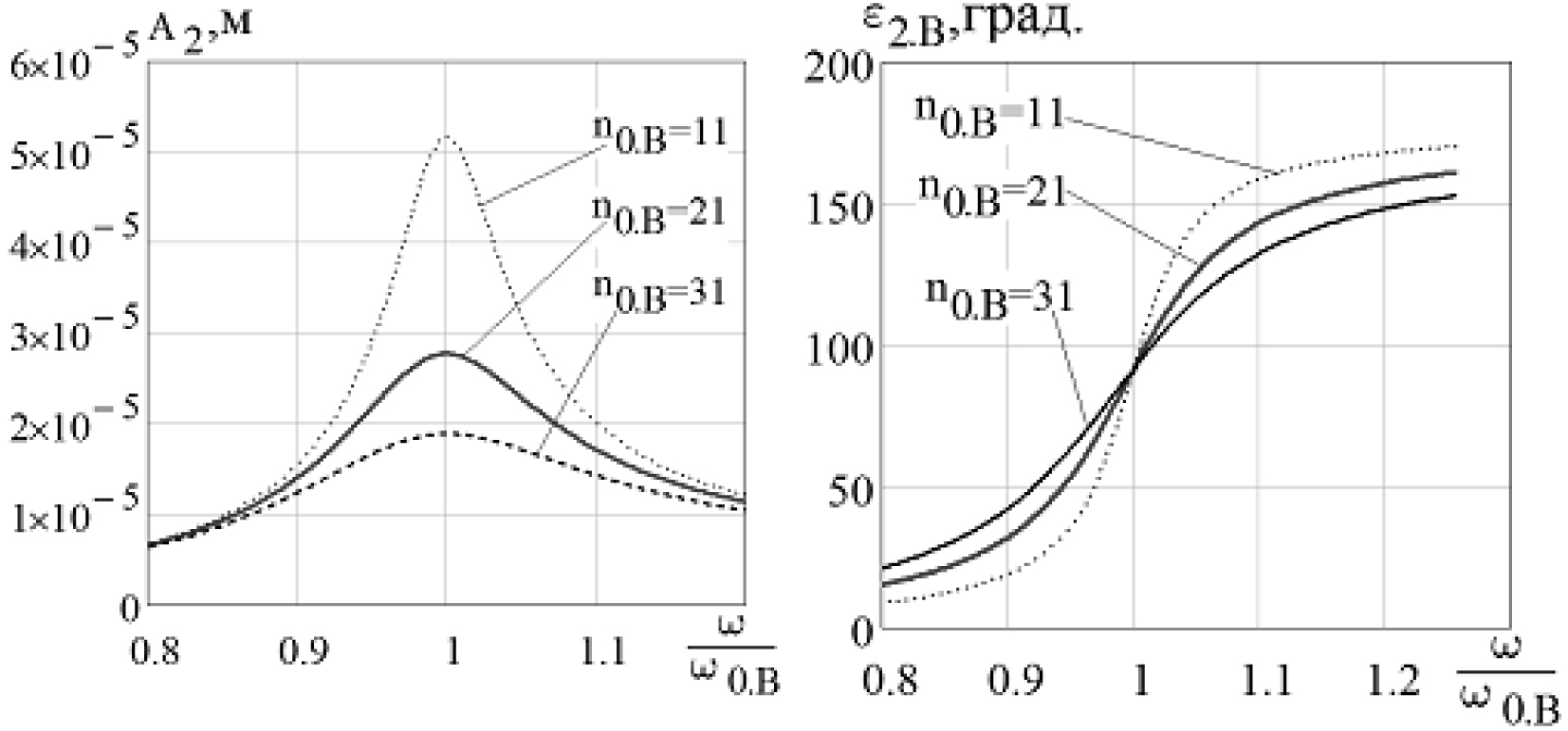
а б
Рис. 4. Графики зависимости амплитуды (а) и угла сдвига фаз (б)
