Программистская модель компьютерной графики

Представление приложения компьютерной графики, его основные компоненты и схема их взаимодействия с внешним миром с точки зрения программиста показано на рис. 3.

Рис. 3 Схема взаимодействия прикладной программы и графической системы.

Необходимые для визуализации исходные данные, содержащие описание изображения, хранятся на компьютере в виде прикладной структуры данных. Внедрением и извлечением информации из прикладной структуры данных управляет прикладная графическая программа. Прикладная программа передает данные и сформированные графические команды в графическую систему (рис. 3) .

Графическая система снабжена пакетом подпрограмм вывода, управляющих конкретным устройством вывода (монитором, принтером и пр.) и обеспечивающих визуализацию изображения этим устройством.

Большинство современных графических программ обеспечивают интерактивность компьютерной графики, т.е. дают пользователю возможность динамически управлять содержанием создаваемого на мониторе изображения с помощью устройств ввода (клавиатуры, мыши, джойстика, и др.). Ввод информации пользователем осуществляется с помощью подпрограмм ввода графической системы, которая передает вводимые данные в прикладную графическую программу.

Координатные системы компьютерной графики

При визуализации объектов на экране монитора или печатающем устройстве необходимо знать его координаты. В компьютерной графике основными являются две системы координат – мировые координаты, описывающие истинное положение объектов в пространстве с заданной точностью, и координаты устройства вывода (например, экрана), на котором осуществляется визуализация.

Цепочку преобразований от мировых к экранным координатам можно представить так, как показано на рис.4.

Видовые координаты применяются в случае необходимости и определяются видом последующего проецирования. При переходе от мировых координат к видовым могут выполняться: смена системы координат (например, правосторонней декартовой на левостороннюю), разворот системы координат в пространстве в соответствии с выбранным направлением проецирования, отсечение координат объекта по выбранному видимому объему.

Координаты проекции получаются после применения операции проецирования к видовым координатам объекта. В случае визуализации двумерных объектов мировые координаты и координаты проекции совпадают (проецирования не требуется).

Для каждого конкретного случая визуализации цепочка преобразований систем координат может сильно отличаться от приведенной. Самый крайний случай – когда мировые координаты объекта сразу заданы в экранных пикселях и никаких преобразований не требуется.

Рис. 4. Переход от мировых координат объекта к экранным.

Геометрические преобразования Двумерные преобразования

Рассмотрим преобразования координат точек на плоскости. На рисунке 5 точка A перенесена в точку B.

Рис. 5. Операция переноса точки A в точку B.

Математически этот перенос можно описать с помощью вектора переноса . Пусть радиус вектор, соответствующий вектору переноса . Тогда переход из точки A в точку B будет соответствовать векторной записи . Отсюда получаем, что для переноса точки в новое положение необходимо добавить к ее координатам некоторые числа, которые представляют собой координаты вектора переноса:

(1)

Масштабированием объектов называется растяжение объектов вдоль соответствующих осей координат относительно начала координат. Эта операция применяется к каждой точке объекта, поэтому можно также говорить о масштабировании точки. При этом, конечно, речь не идет об изменении размеров самой точки. Масштабирование достигается умножением координат точек на некоторые константы. В том случае, когда эти константы равны между собой, масштабирование называется однородным.

Рис. 6. Операция масштабирования .

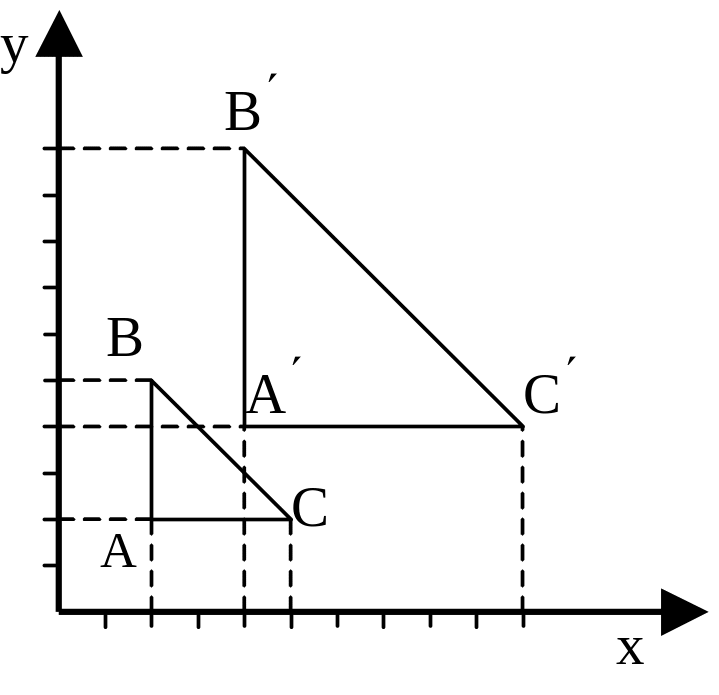
На рис.6 приведен пример однородного масштабирования треугольника ABC. После применения операции однородного масштабирования с коэффициентом 2 он переходит в треугольник A^'B^'C^'. Обозначим матрицу масштабирования

. (2)

Для точек A и A^' операция масштабирования в матричном виде будет выглядеть следующим образом:

. (3)

Или в матричном виде

A^' = A S (4)

Рассмотрим далее операцию вращения точки на некоторый угол относительно начала координат. На рисунке 7 точка A = (x, y) переходит в точку B = (x^', y^') поворотом на угол .

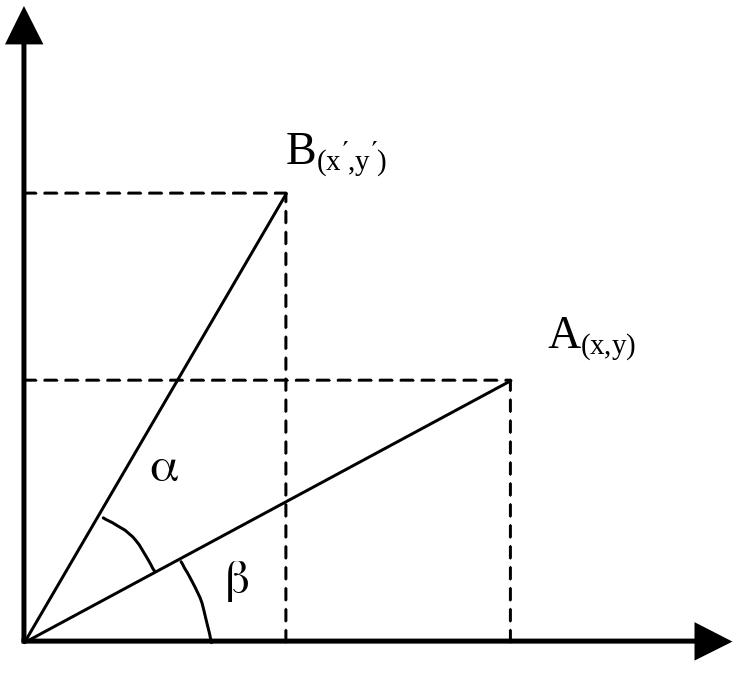
Рис. 7. Операция поворота точки A на угол .

Найдем преобразование координат точки А в точку В. Обозначим  угол, который составляет радиус-вектор с осью Оx. Пусть r – длина радиус-вектора , тогда