
Функции нескольких переменных
Найти область определения функции
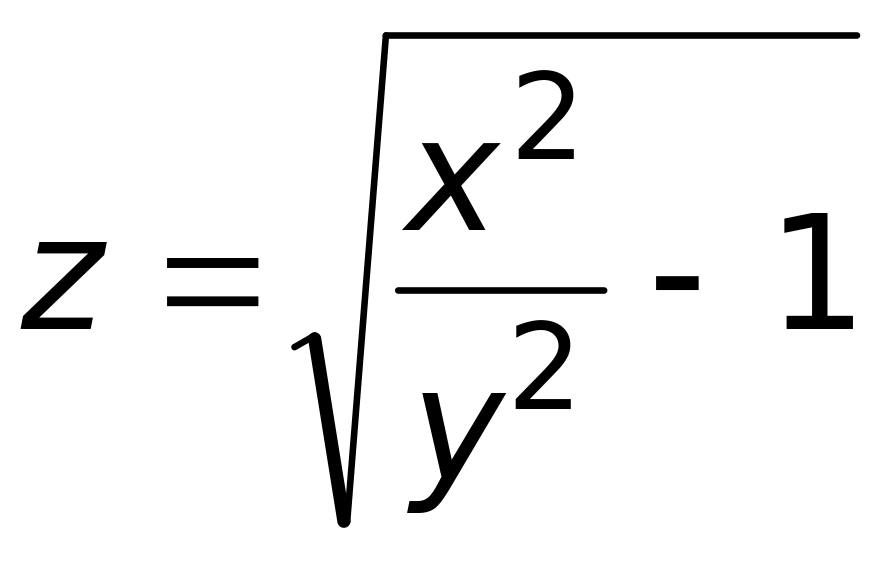
О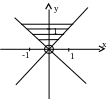
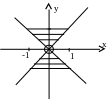 твет:
а) б)
твет:
а) б)
в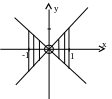
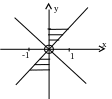 ) (верный
ответ) г)
) (верный
ответ) г)
Н
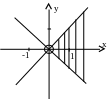
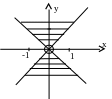 айти
область определения функции
айти
область определения функции
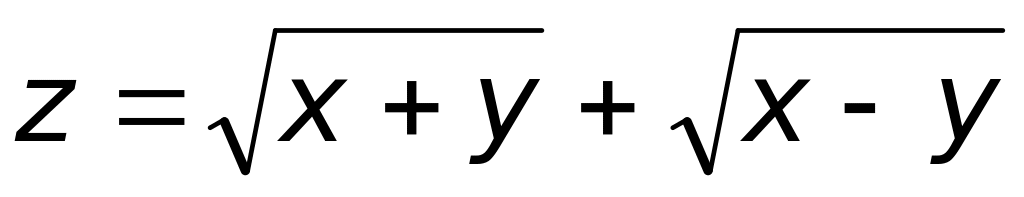 Ответ:
а) (верный ответ) б)
Ответ:
а) (верный ответ) б)
в
 ) г)
) г)
Для функции двух переменных
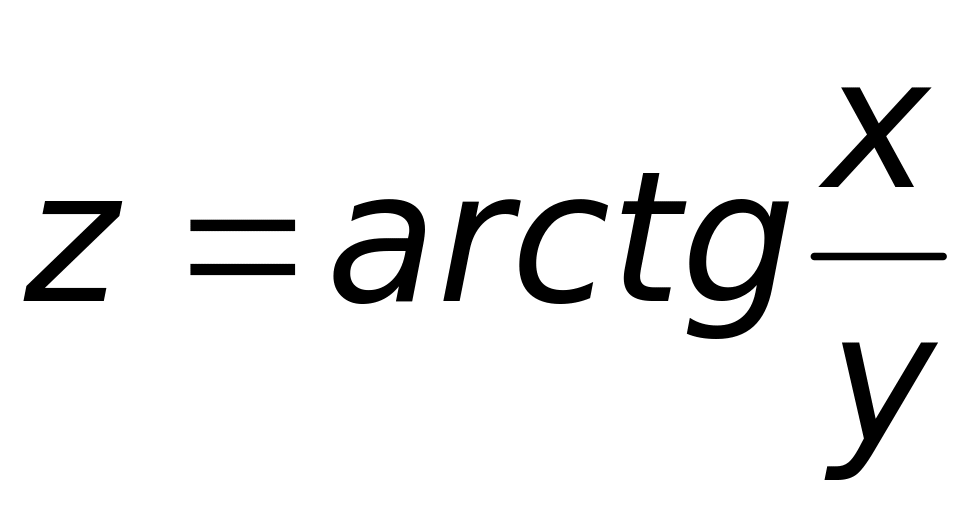 смешанная производная второго порядка
равна:
Ответ: 1)
смешанная производная второго порядка
равна:
Ответ: 1)
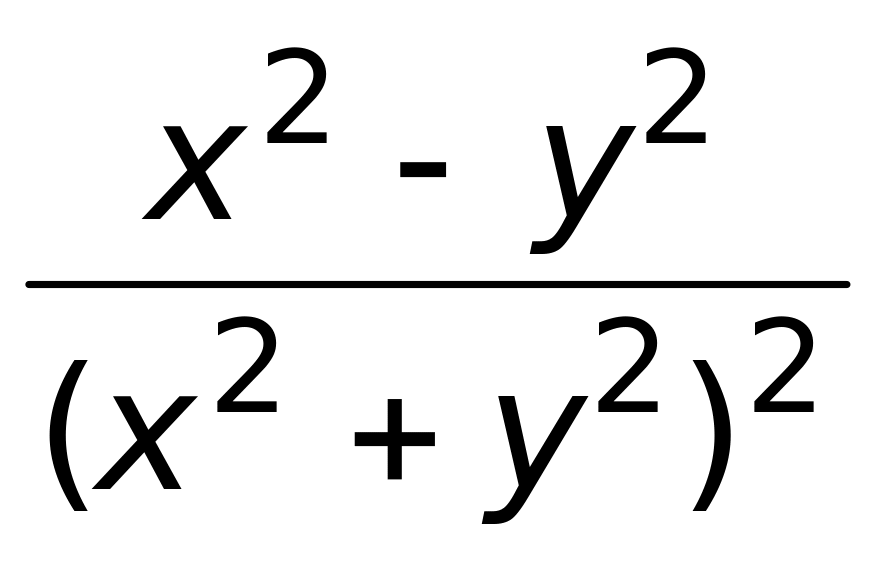 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.Найти
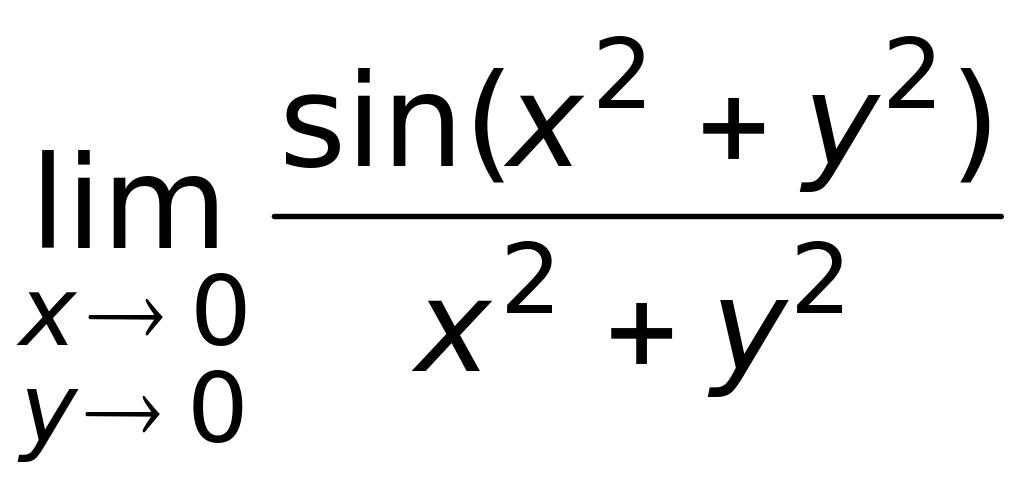 Ответ: а) не существует;
б) 0;
в)
3;
г) 1(верный ответ).
Ответ: а) не существует;
б) 0;
в)
3;
г) 1(верный ответ).Если
 ,
то дифференциал второго порядка
,
то дифференциал второго порядка
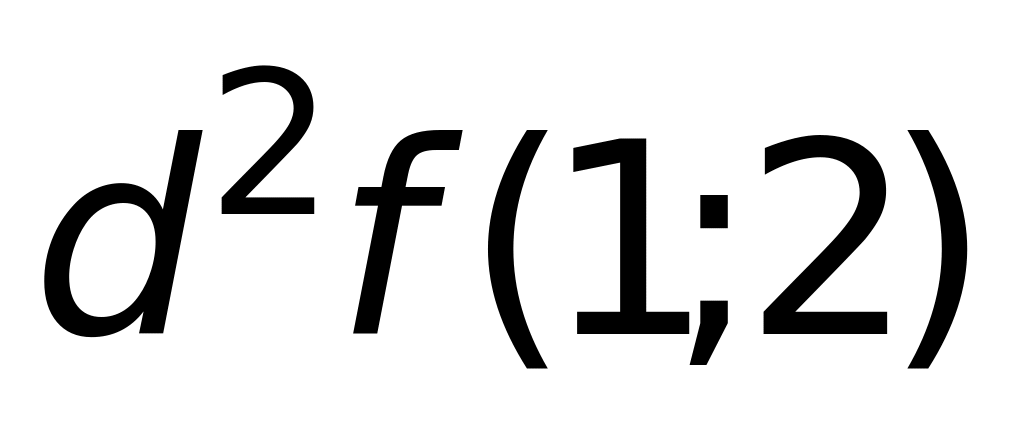 равен:
Ответ: 1) 0;
2)
равен:
Ответ: 1) 0;
2)
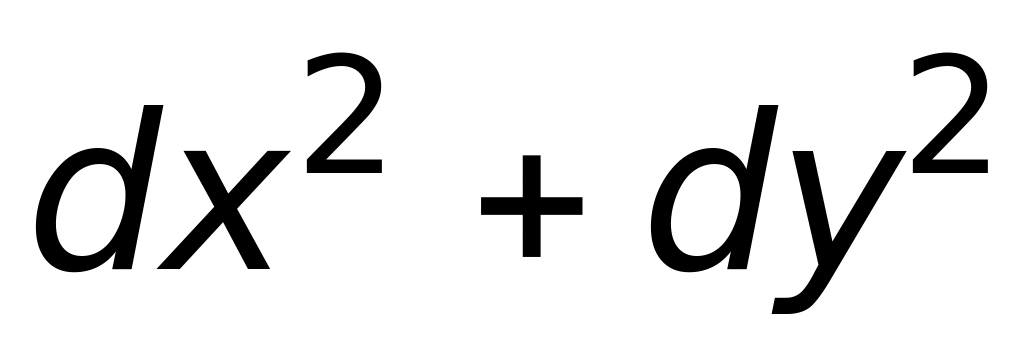 ;
3)
;
3)
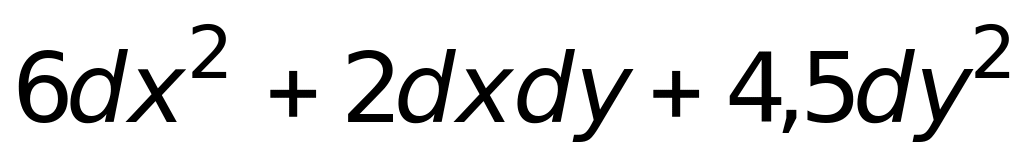 (верный ответ);
4) другой ответ.
(верный ответ);
4) другой ответ.Если функция
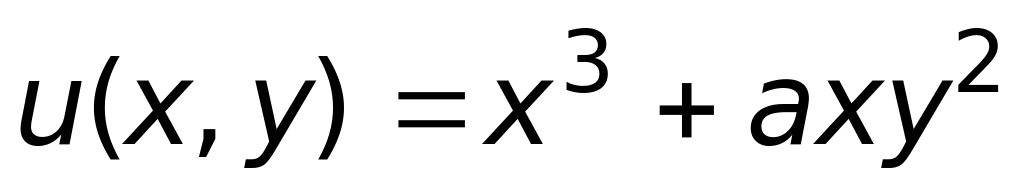 удовлетворяет уравнению
удовлетворяет уравнению
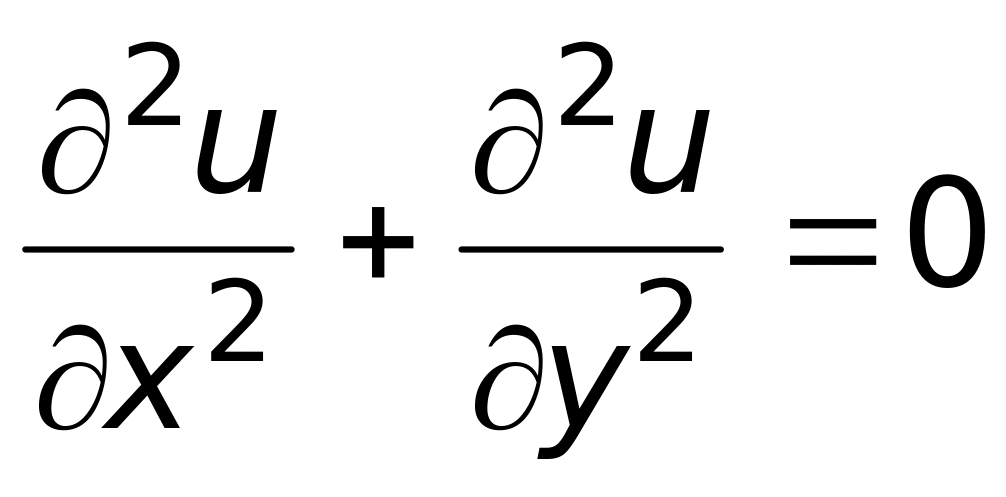 ,
то значение постоянной а
равно:
Ответ:
1) 3;
2) –3 (верный ответ);
3) 1;
4)
2.
,
то значение постоянной а
равно:
Ответ:
1) 3;
2) –3 (верный ответ);
3) 1;
4)
2.Частные производные
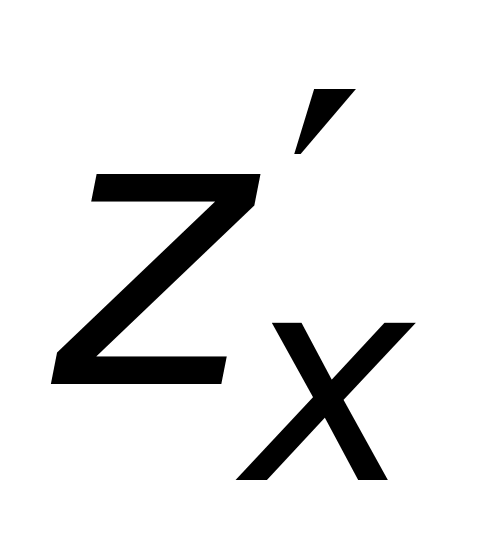 и
и
 неявной функции
неявной функции
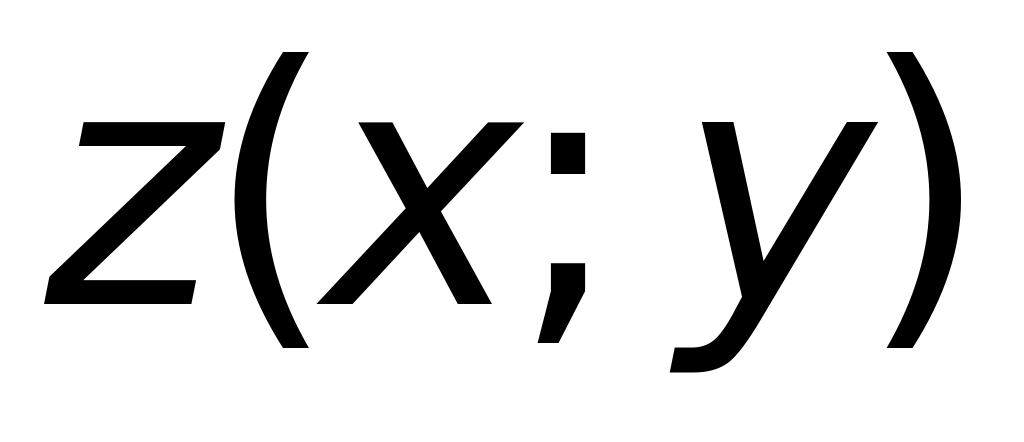 ,
заданной уравнением
,
заданной уравнением
 в точке
в точке
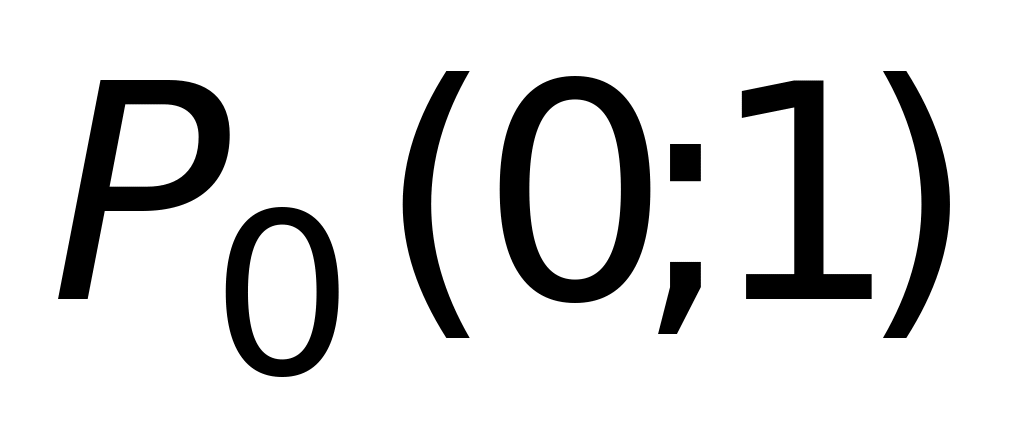 равны:
Ответ: 1) (-3;-1) (верный ответ);
2)
равны:
Ответ: 1) (-3;-1) (верный ответ);
2)
 ;
3) (0;1);
4) (1;3).
;
3) (0;1);
4) (1;3).Если
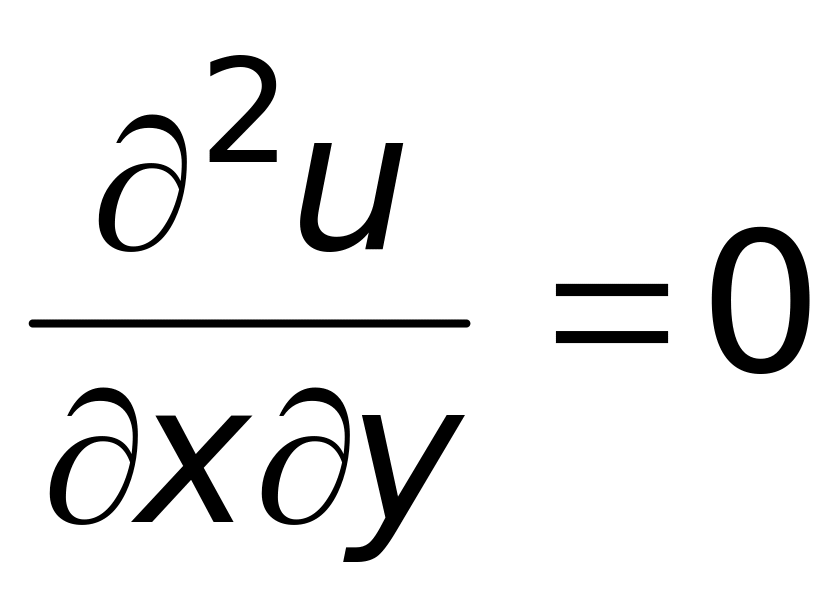 ,
то общий вид функции
,
то общий вид функции
 :
Ответ:
1)
:
Ответ:
1)
 ;
2)
;
2)
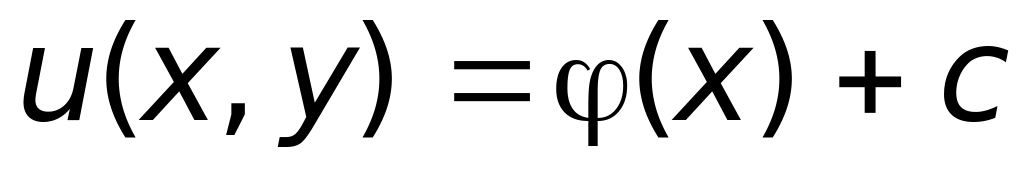 ;
3)
;
3)
 (верный ответ);
4)
(верный ответ);
4)
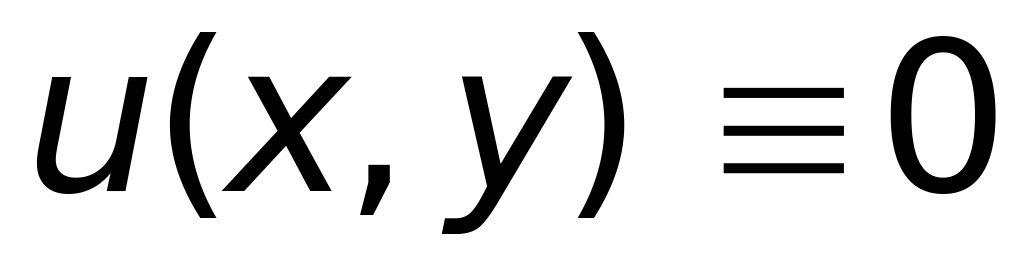 .
.Если функция
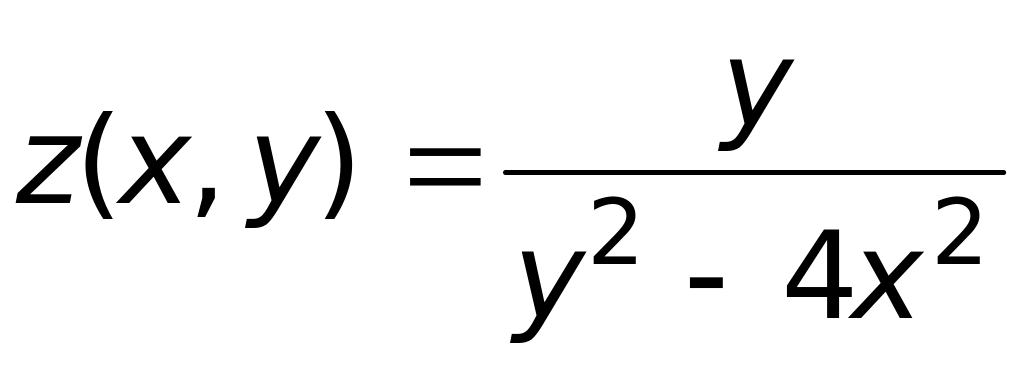 ,
то выражение
,
то выражение
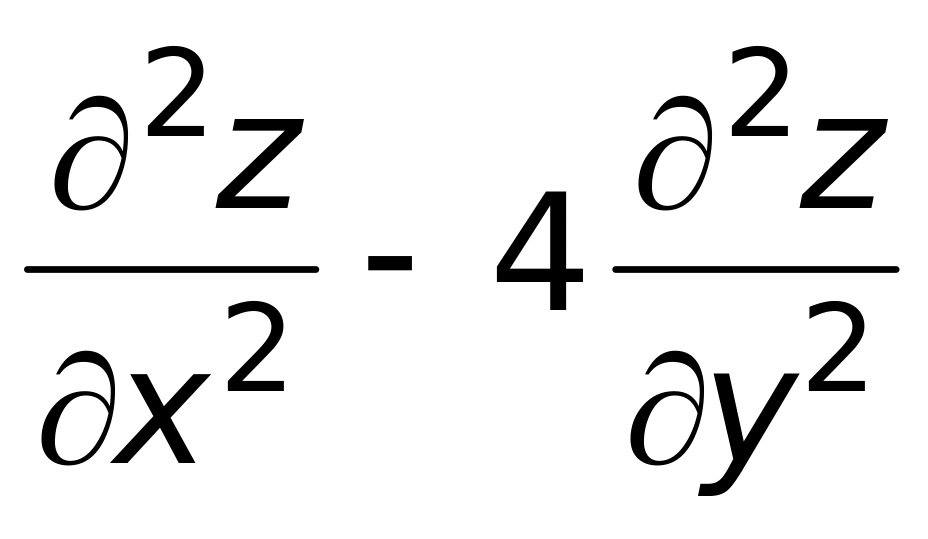 равно:
Ответ: 1) 0 (верный ответ);
2)
равно:
Ответ: 1) 0 (верный ответ);
2)
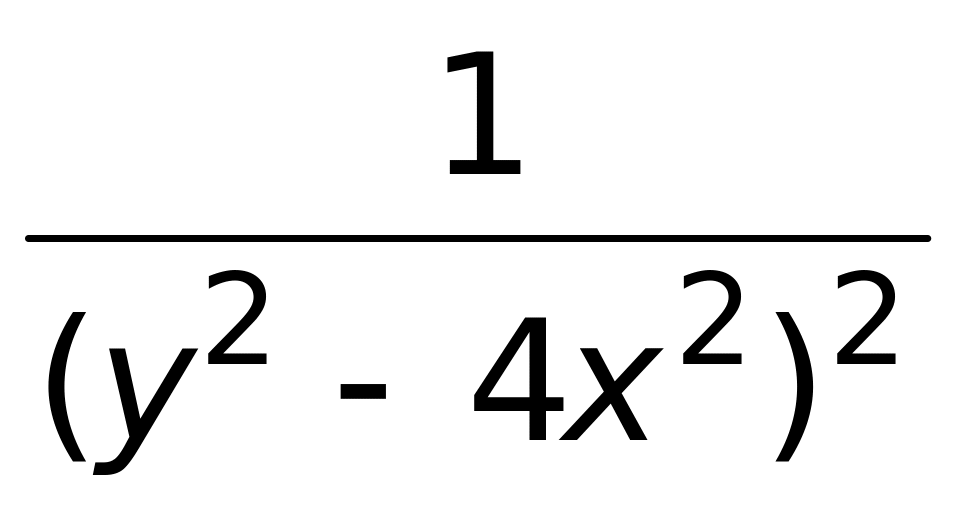 ;
3)
;
3)
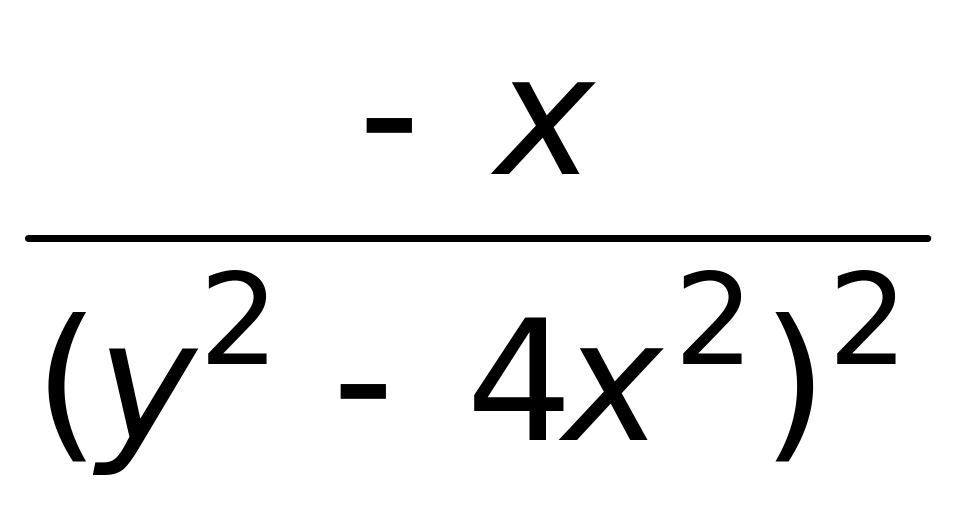 ;
4)
;
4)
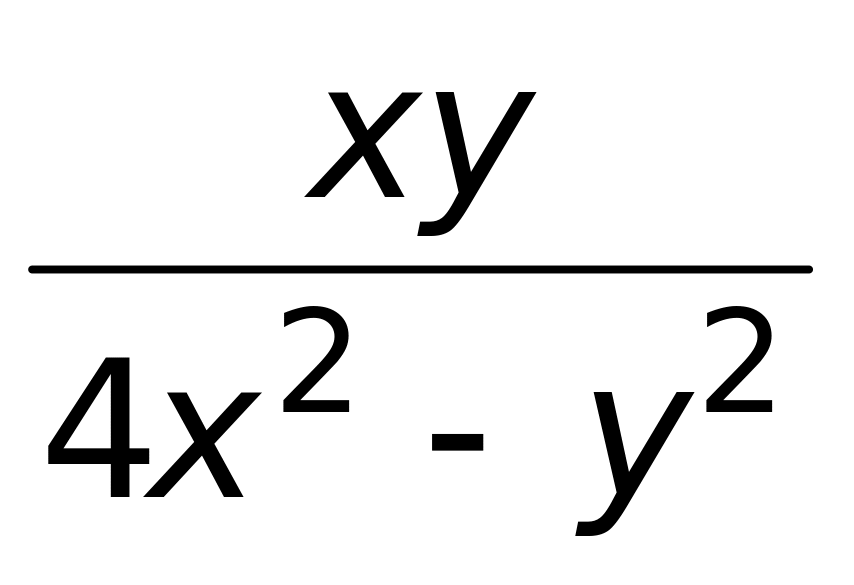 .
.Вычислить интеграл
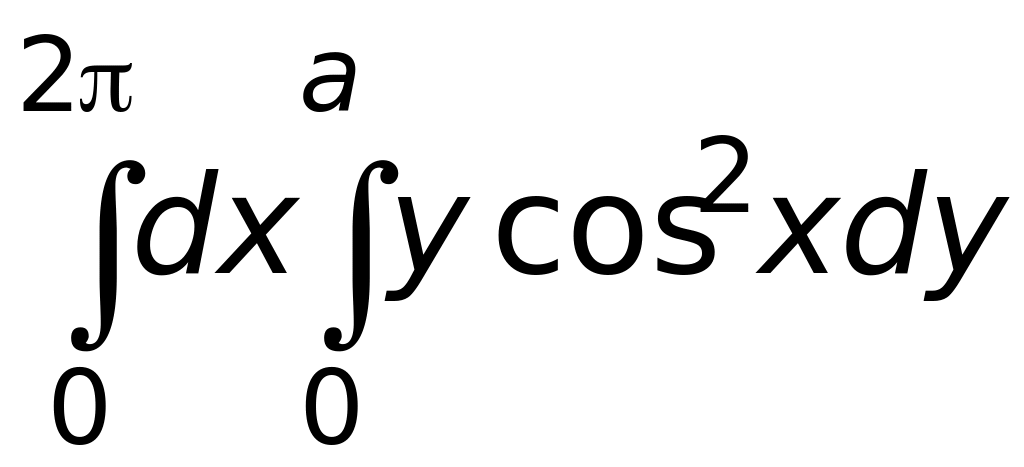 Ответ:
1)
Ответ:
1)
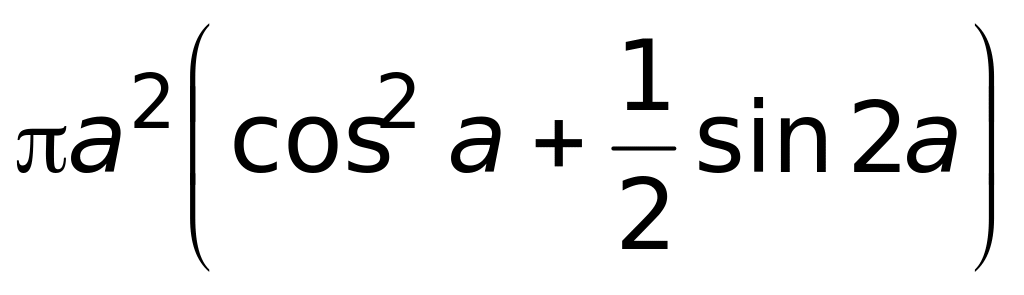 ;
2)
;
2)
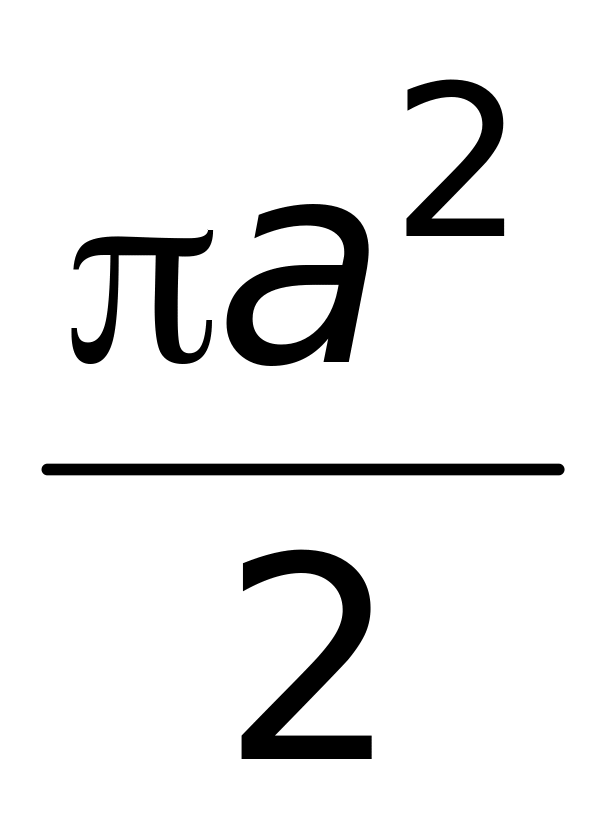 (верный ответ);
3)
(верный ответ);
3)
 ;
4)
;
4)
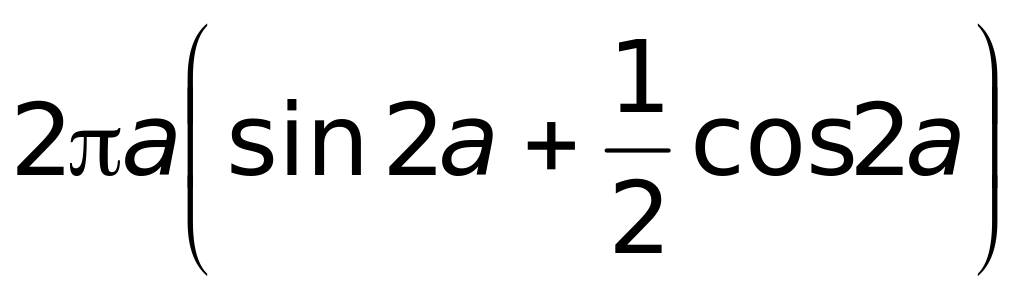 .
.Вычислить интеграл
 Ответ:
1)
Ответ:
1)
 ;
2)
;
2)
 ;
3)
;
3)
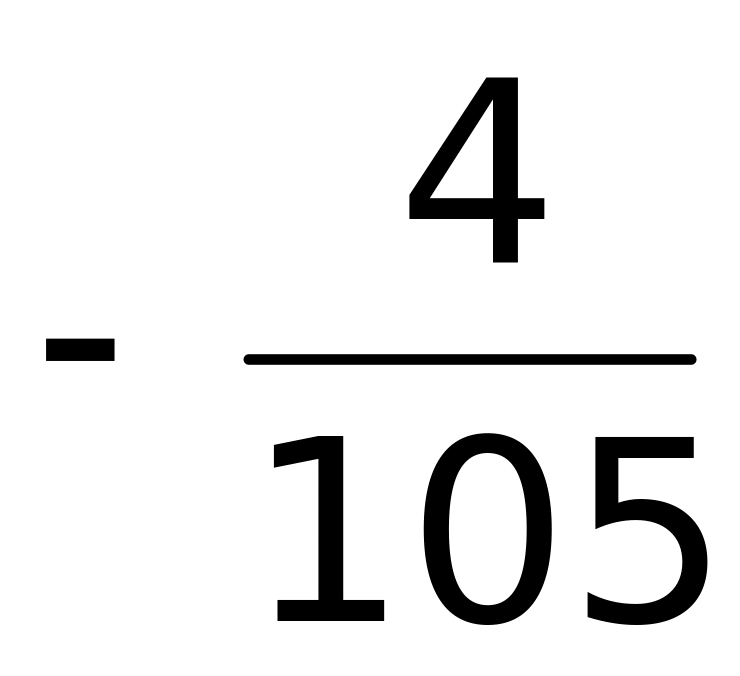 ;
4)
;
4)
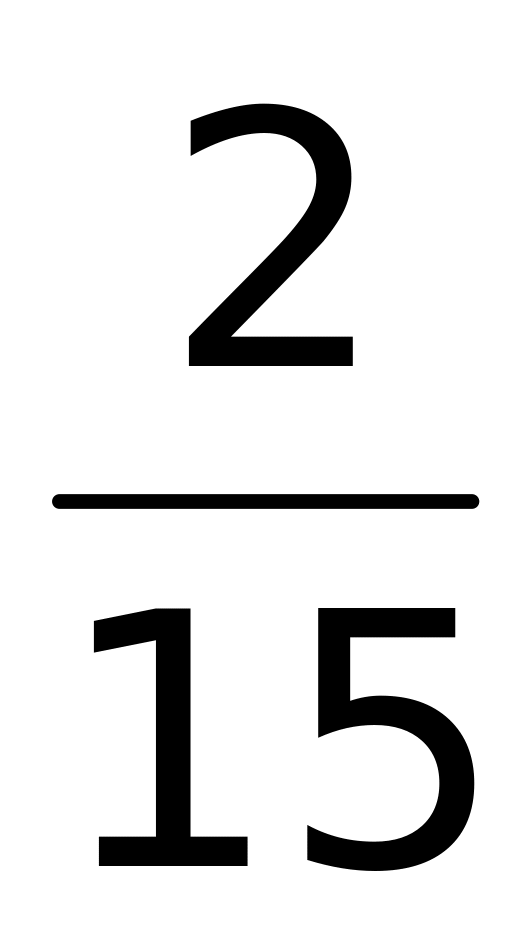 (верный ответ).
(верный ответ).Вычислить интеграл
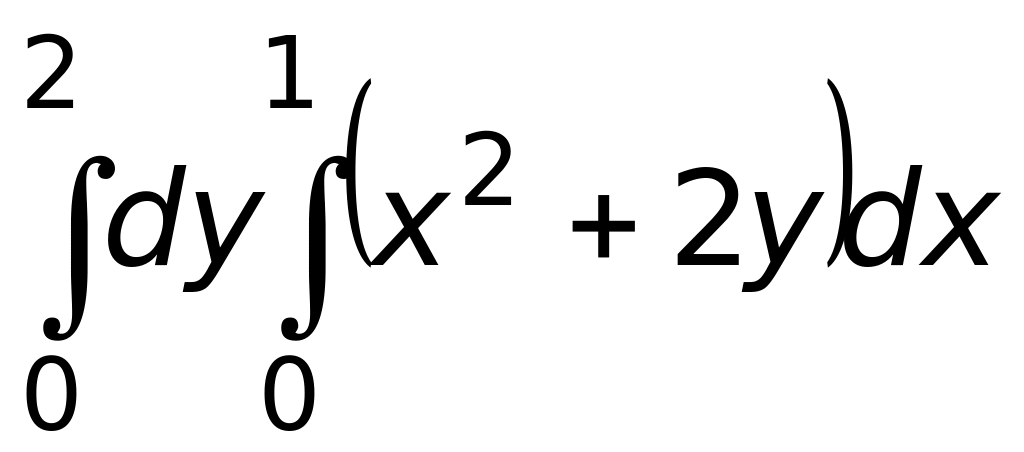 Ответ:
1)
Ответ:
1)
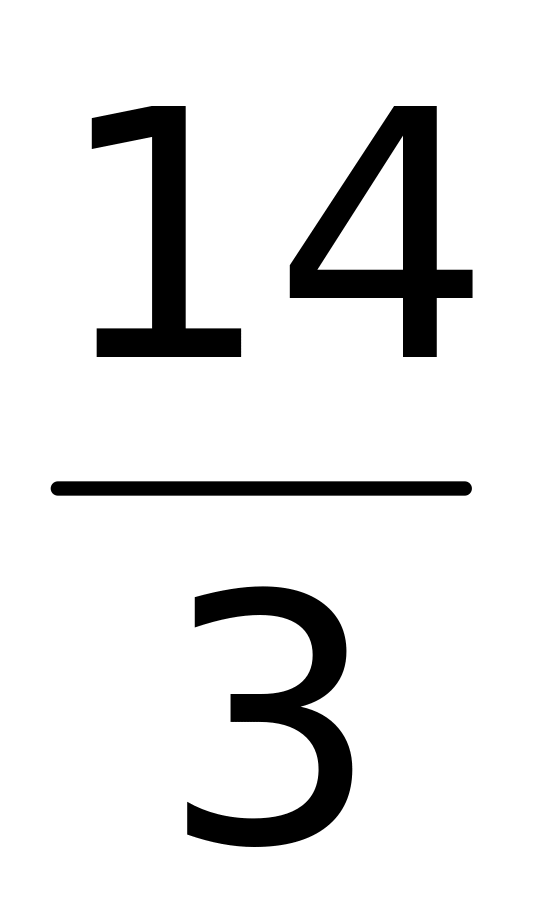 (верный ответ);
2) 1;
3)
(верный ответ);
2) 1;
3)
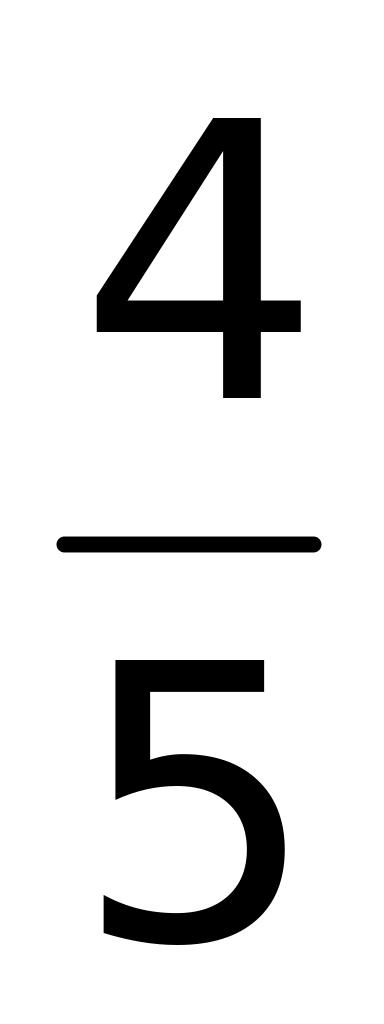 ;
4)
;
4)
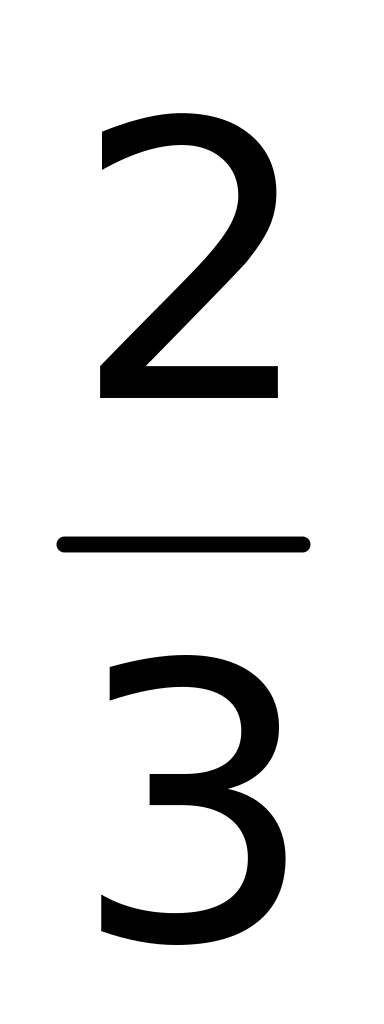 .
.Вычислить интеграл
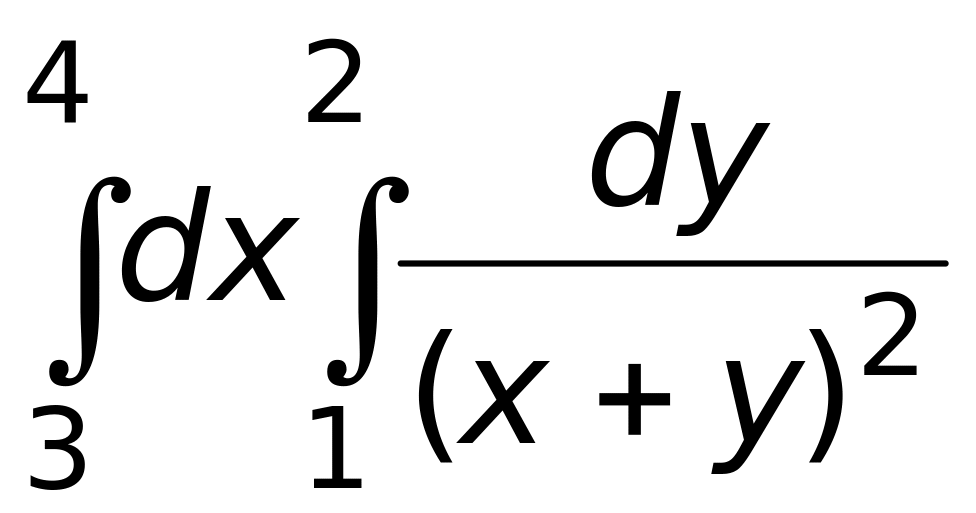 Ответ:
1)
Ответ:
1)
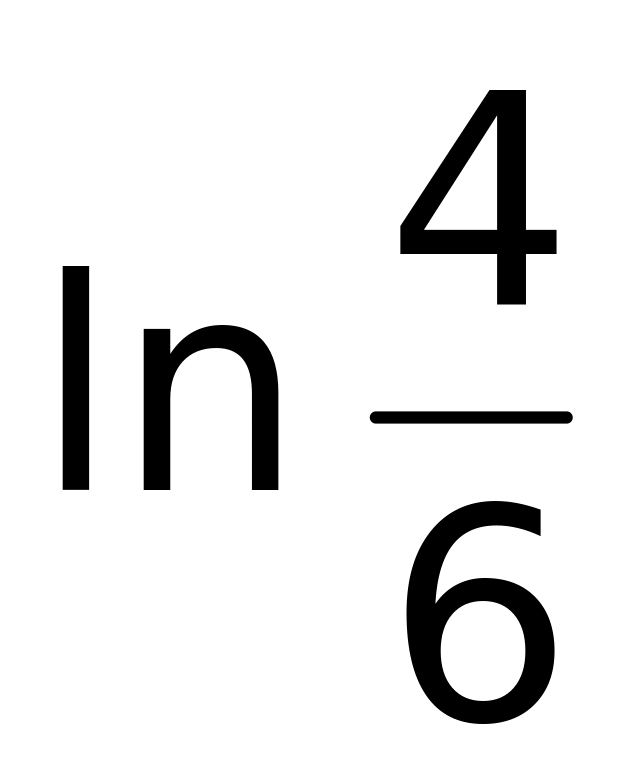 ;
2)
;
2)
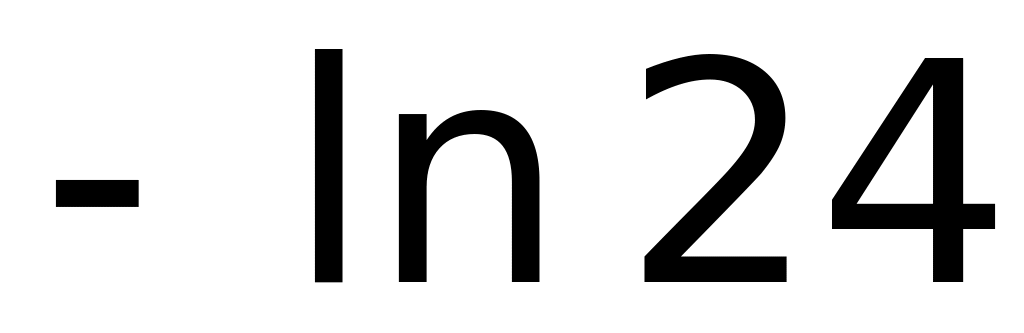 ;
3)
;
3)
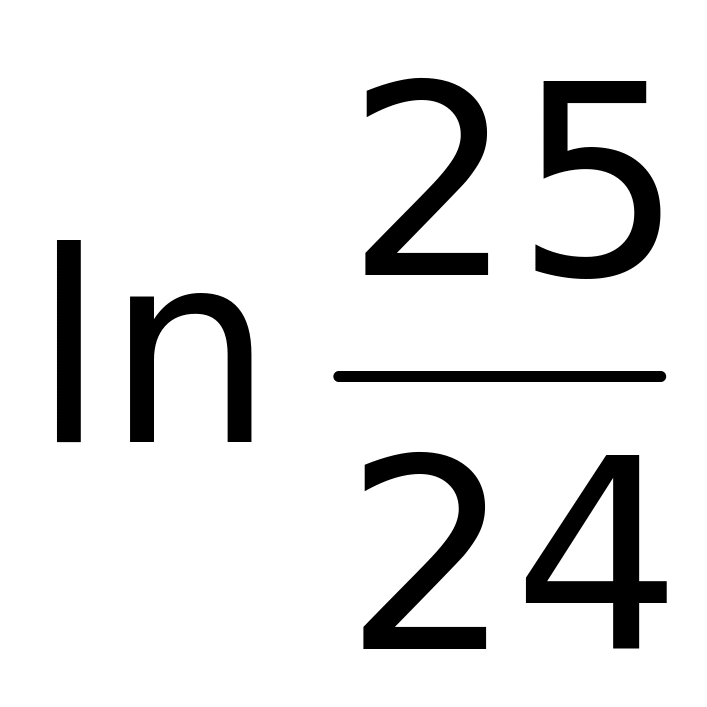 (верный ответ);
4)
(верный ответ);
4)
 .
.Вычислить интеграл
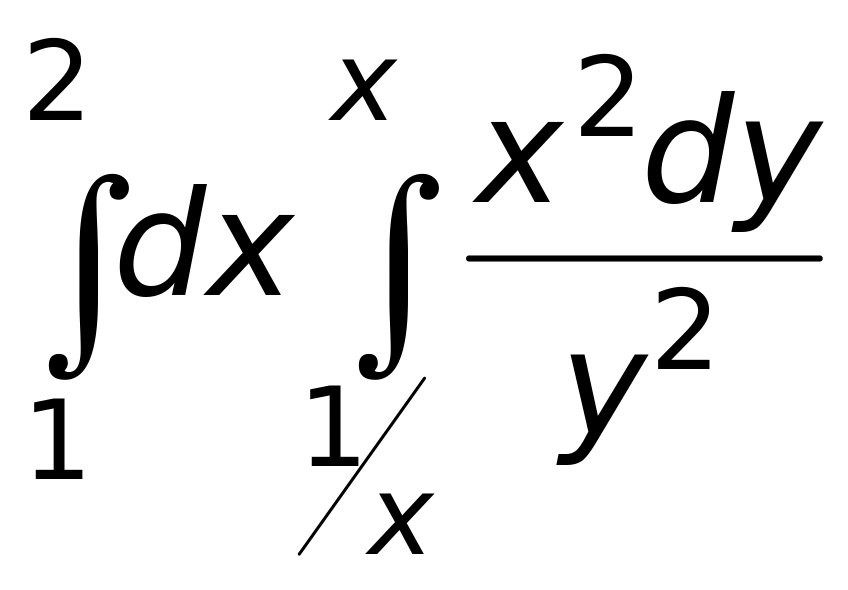 Ответ:
1)
Ответ:
1)
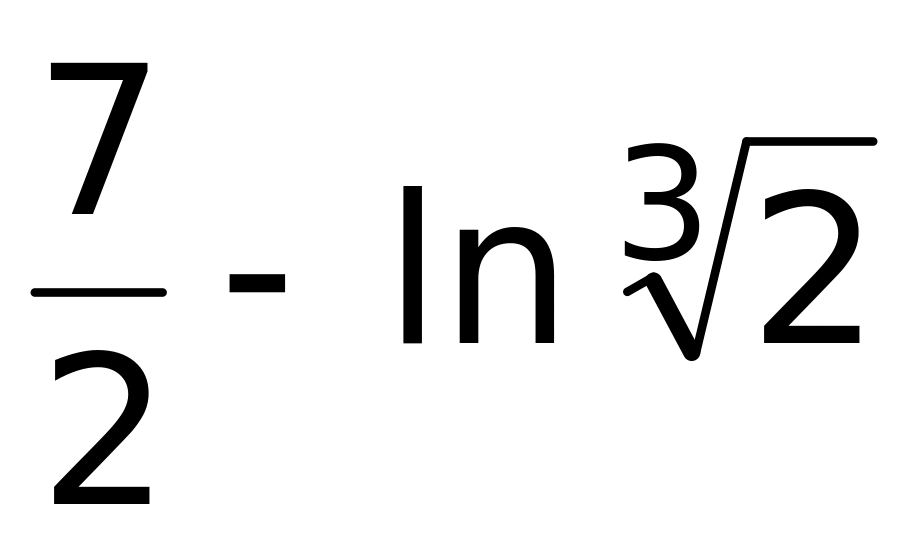 ;
2)
;
2)
 (верный ответ);
3) –3;
4)
(верный ответ);
3) –3;
4)
 .
.Вычислить интеграл
 Ответ:
1)
Ответ:
1)
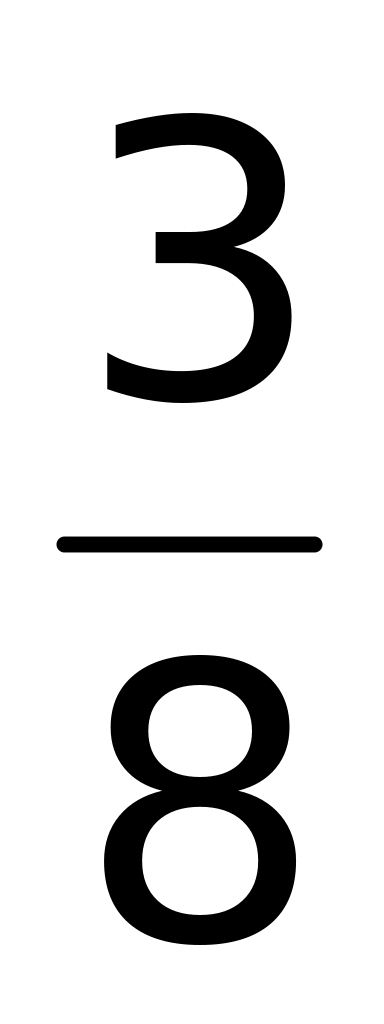 ;
2)
;
3)
;
2)
;
3)
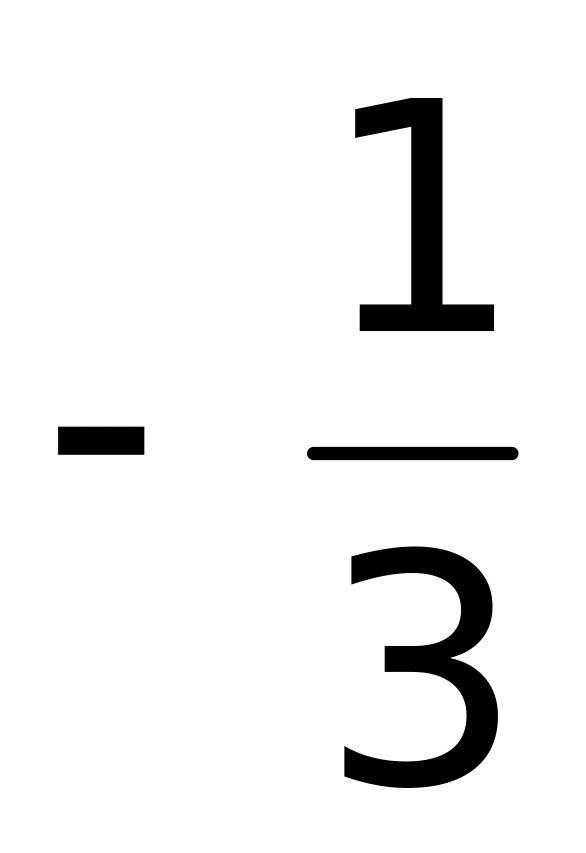 ;
4)
(верный ответ).
;
4)
(верный ответ).Вычислить интеграл
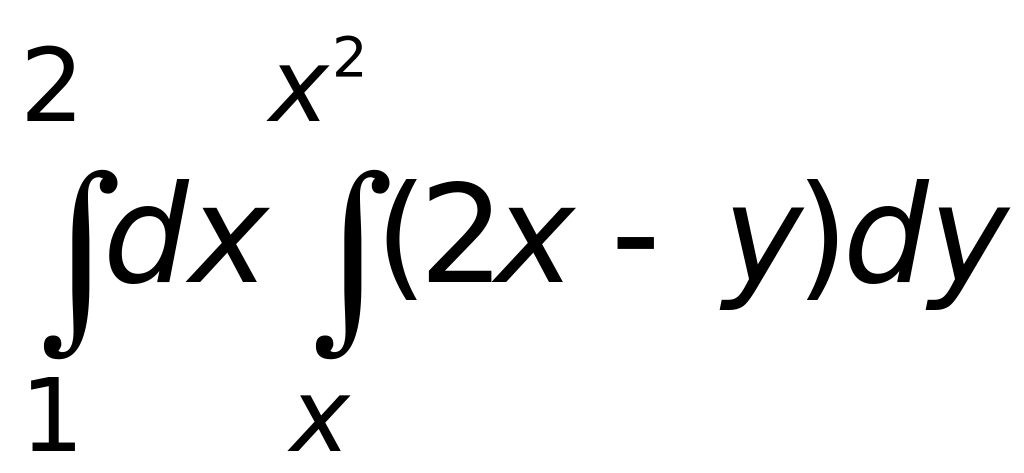 Ответ:
1) – 2,85;
2) 0,9 (верный ответ);
3)
Ответ:
1) – 2,85;
2) 0,9 (верный ответ);
3)
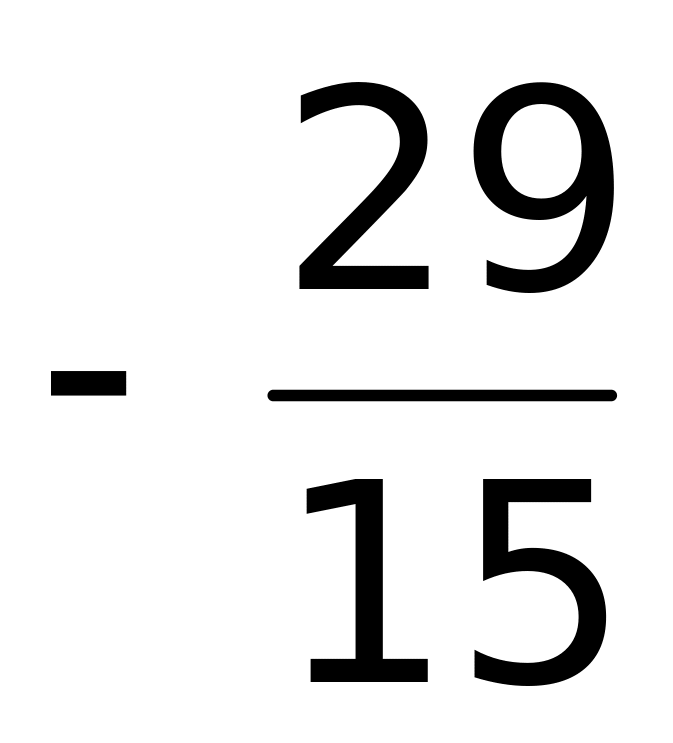 ;
4) – 0,9.
;
4) – 0,9.Вычислить интеграл
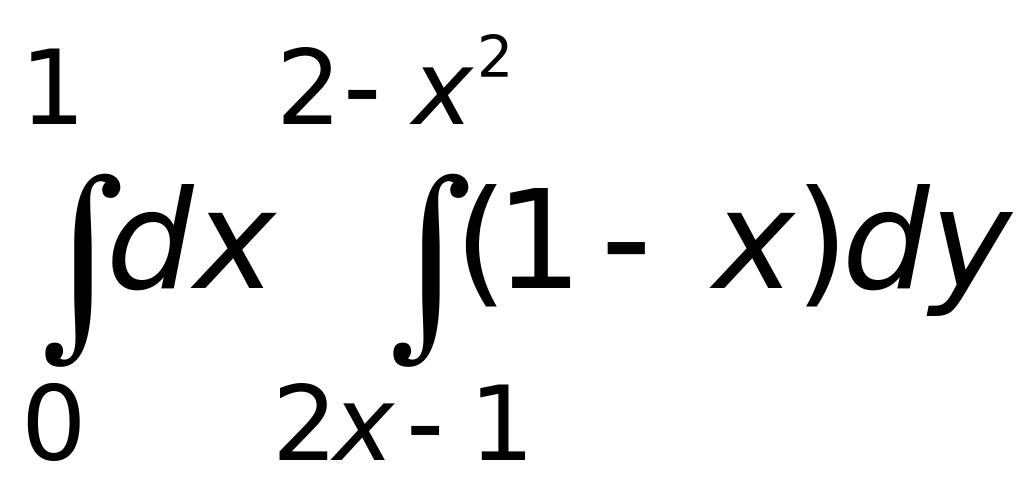 Ответ:
1)
Ответ:
1)
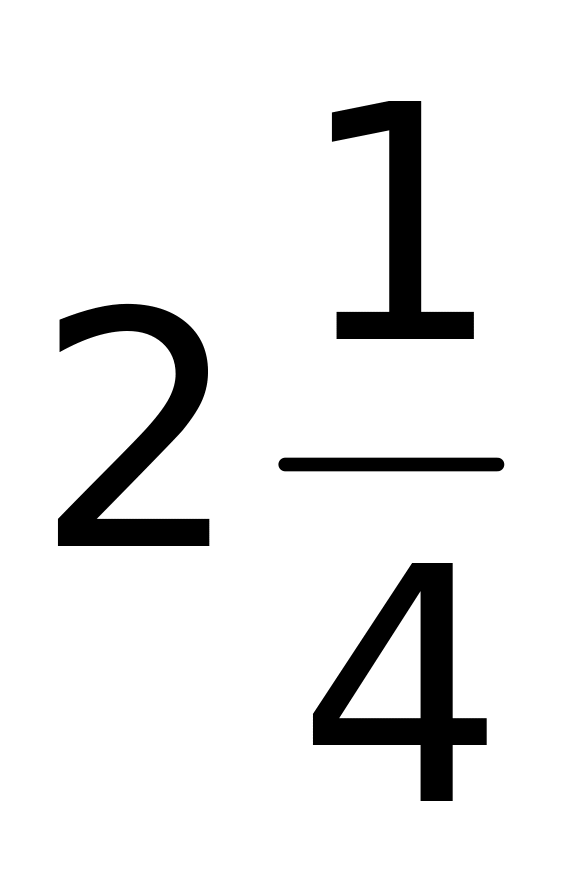 ;
2)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
 ;
4)
;
4)
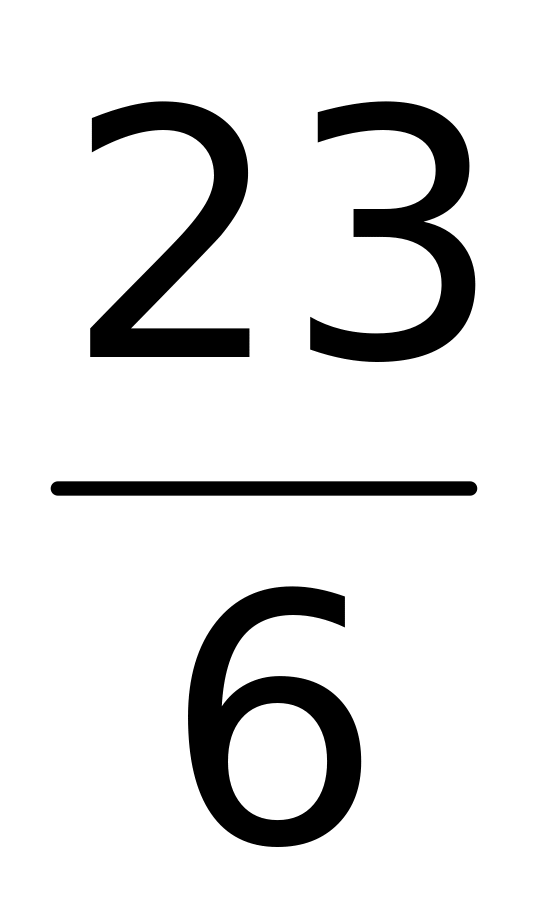 .
.Вычислить интеграл
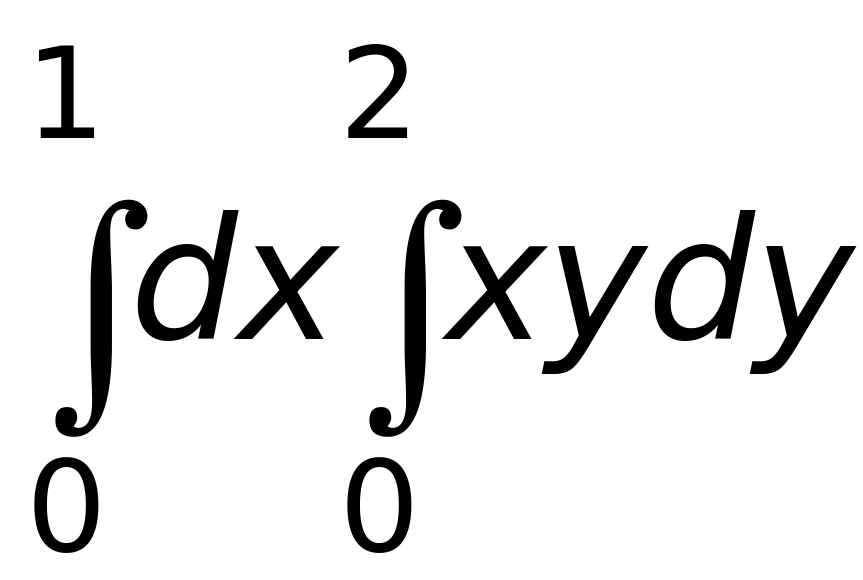 Ответ:
1) 1 (верный ответ);
2)
;
3) 2;
4) – 1.
Ответ:
1) 1 (верный ответ);
2)
;
3) 2;
4) – 1.Вычислить интеграл
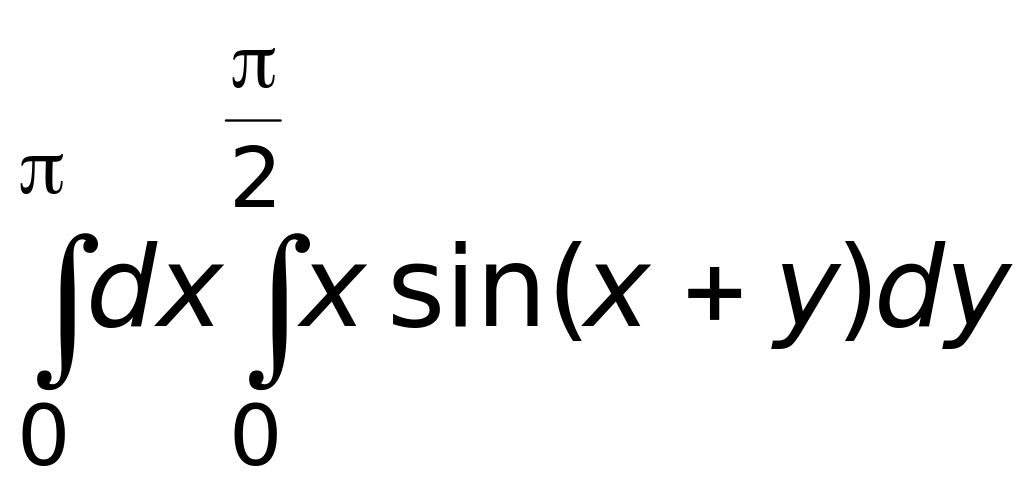 Ответ:
1) – 1;
2) 1 (верный ответ);
3) – 2;
4)
2.
Ответ:
1) – 1;
2) 1 (верный ответ);
3) – 2;
4)
2.Вычислить интеграл
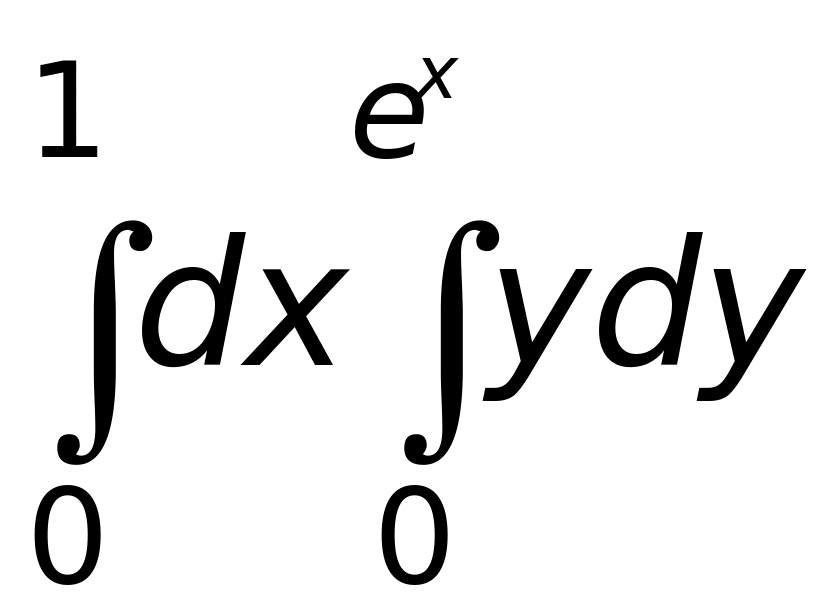 Ответ:
1)
Ответ:
1)
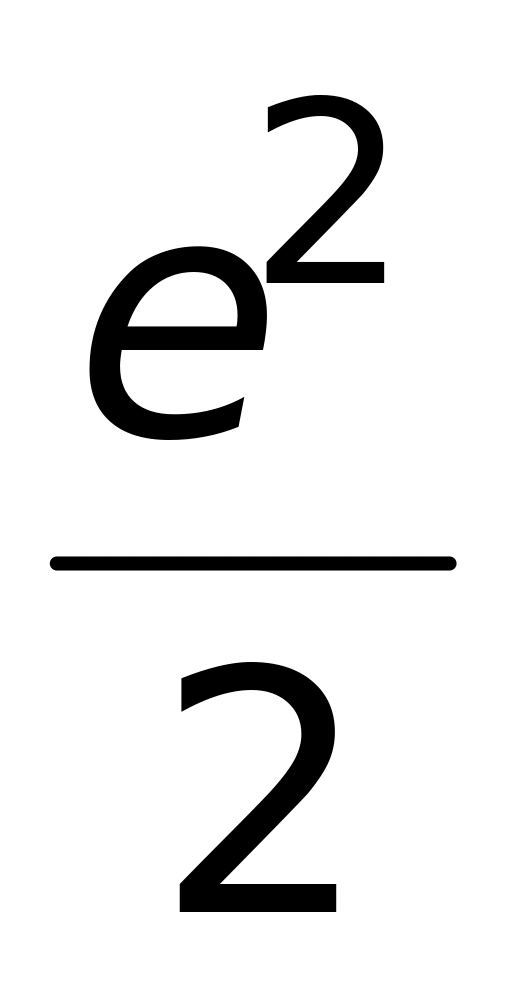 ;
2)
;
2)
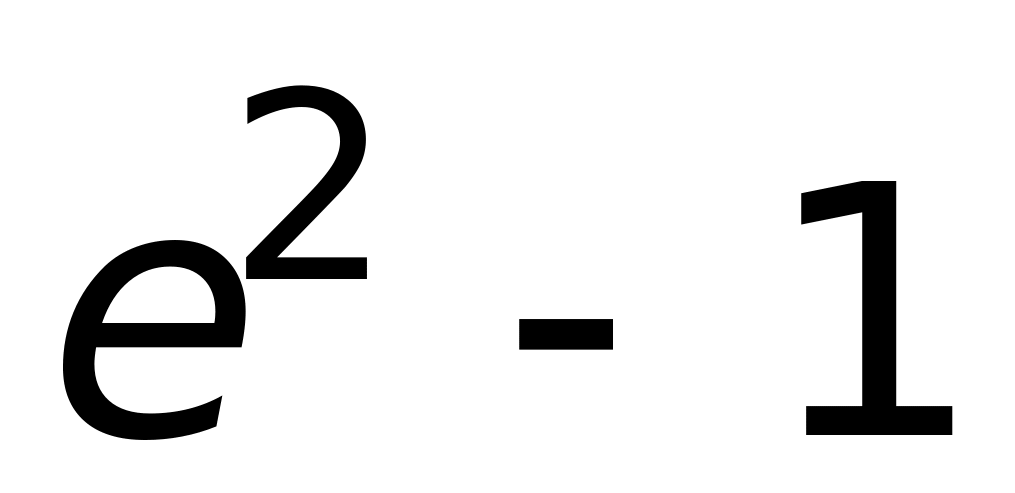 ;
3)
;
3)
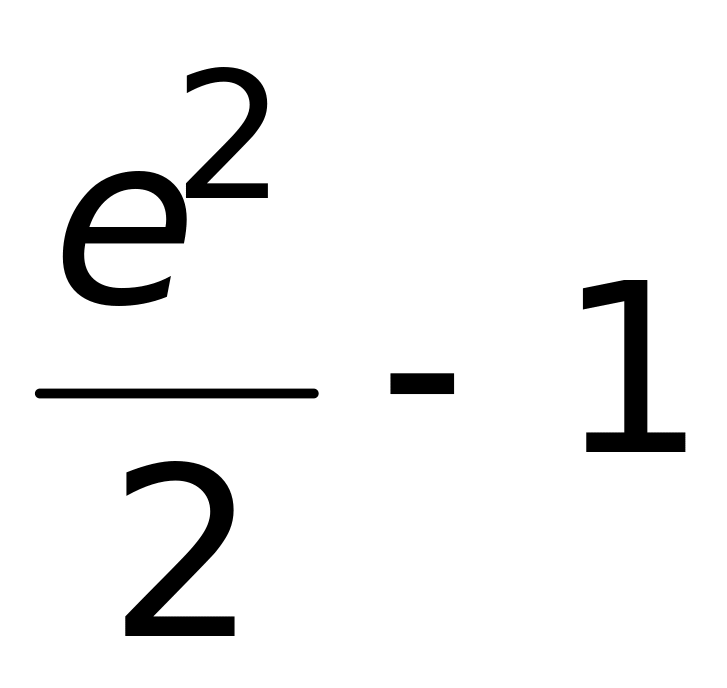 ;
4)
;
4)
 (верный ответ).
(верный ответ).Вычислить интеграл
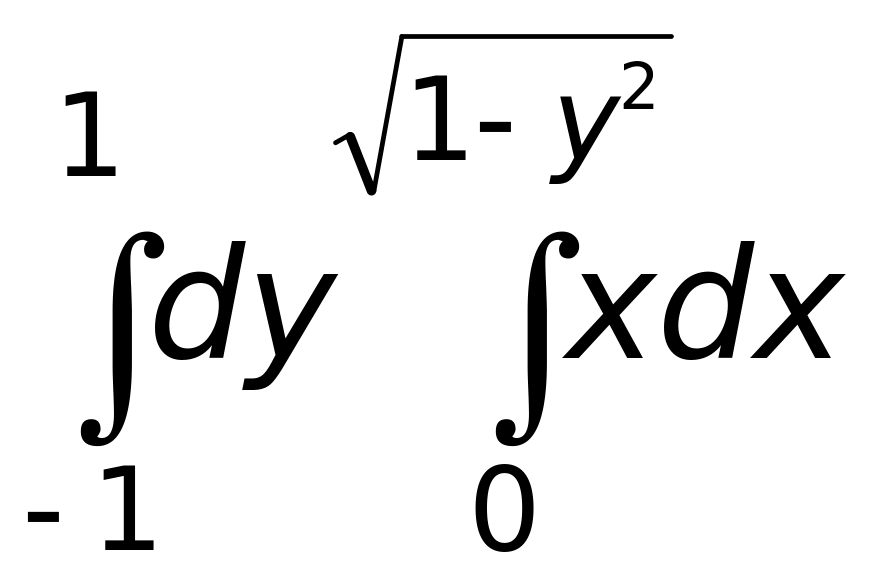 Ответ:
1) 0;
2)
;
3)
(верный ответ);
4) 1.
Ответ:
1) 0;
2)
;
3)
(верный ответ);
4) 1.Вычислить интеграл
 Ответ:
1) 36;
2) 9 (верный ответ);
3) 18;
4)
15.
Ответ:
1) 36;
2) 9 (верный ответ);
3) 18;
4)
15.Вычислить интеграл
 Ответ:
1) – 2 (верный ответ);
2) 2;
3) – 1;
4)
0.
Ответ:
1) – 2 (верный ответ);
2) 2;
3) – 1;
4)
0.Вычислить интеграл
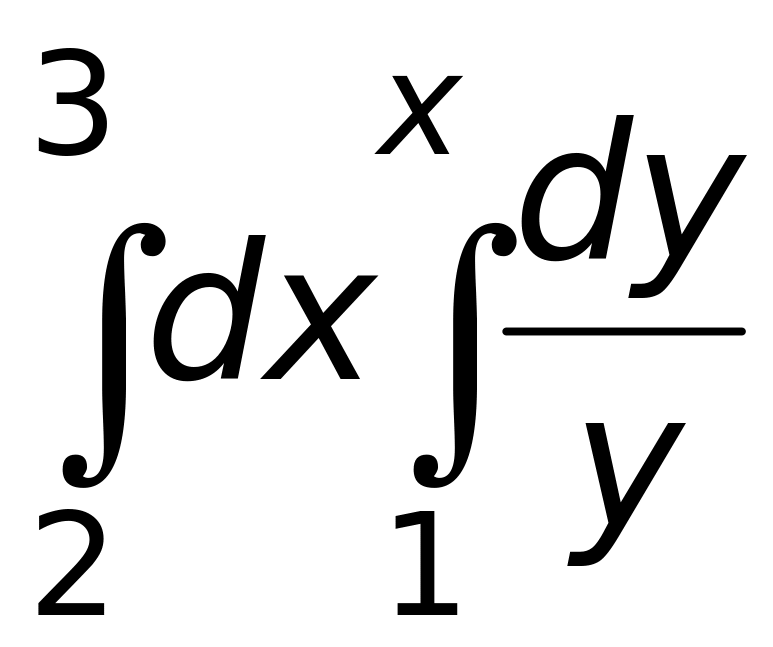 Ответ:
1)
Ответ:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
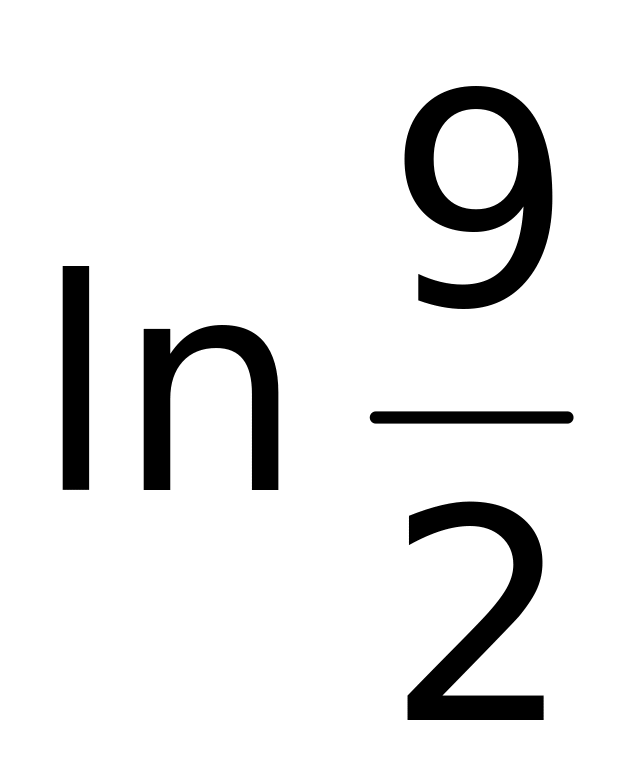 (верный ответ).
(верный ответ).
Вычислить полный дифференциал функции

Ответ: а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() (верный
ответ);
г)
(верный
ответ);
г)
![]() .
.
Вычислить полный дифференциал функции
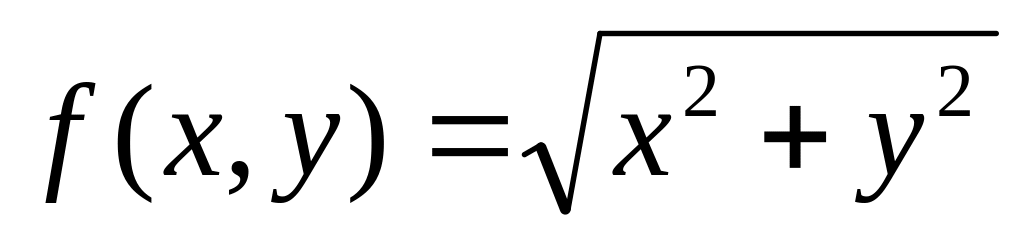
Ответ: а)![]() ;
б)
;
б)
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Вычислить полный дифференциал функции
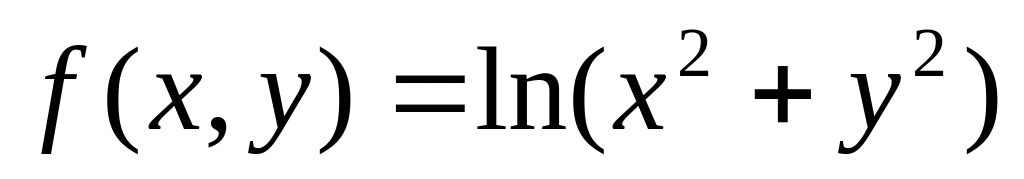
Ответ: а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() (верный
ответ).
(верный
ответ).
Вычислить полный дифференциал функции

Ответ: а)![]() ;
б)
;
б)
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Вычислить полный дифференциал функции
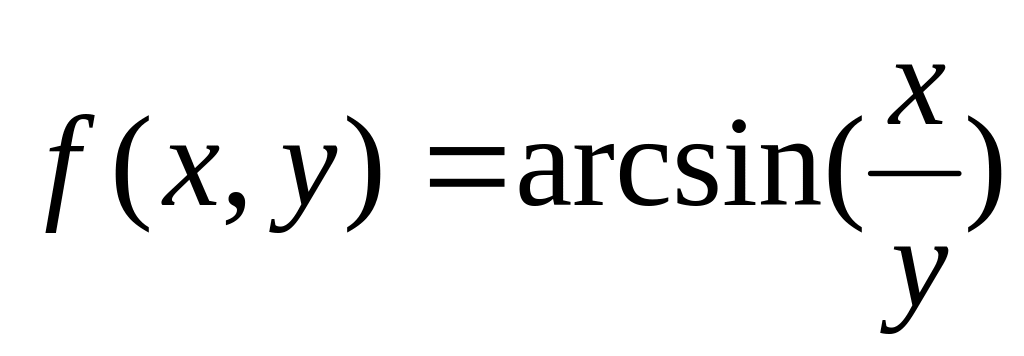
Ответ: а)![]() (верный ответ);
б)
(верный ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Вычислить значение производной сложной функции
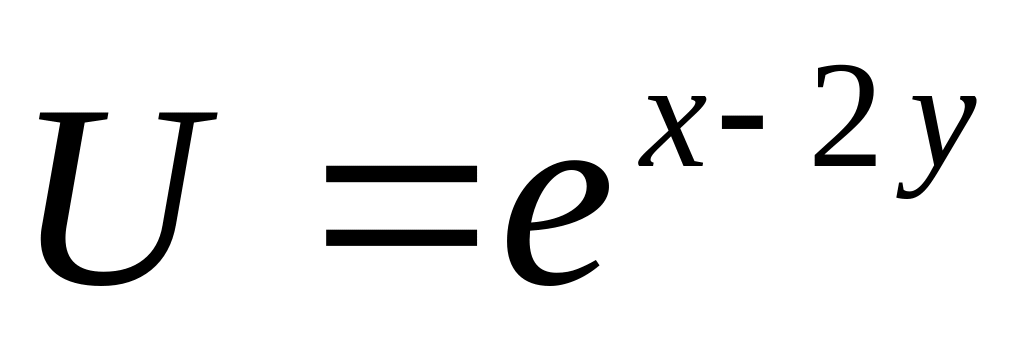 ,
где
,
где
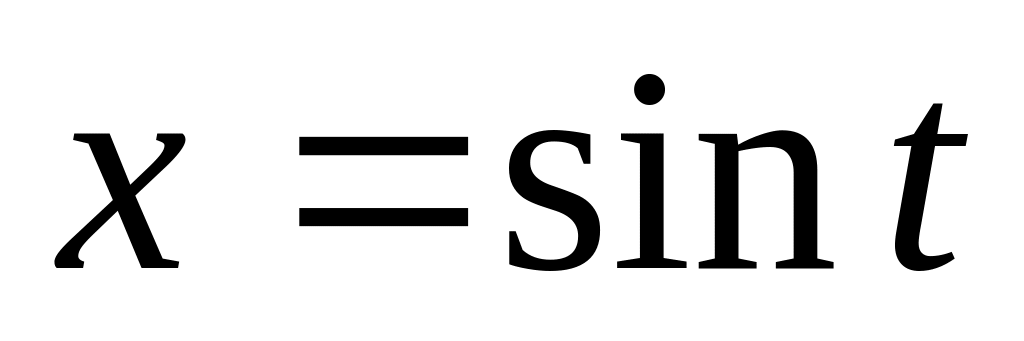 ,
,
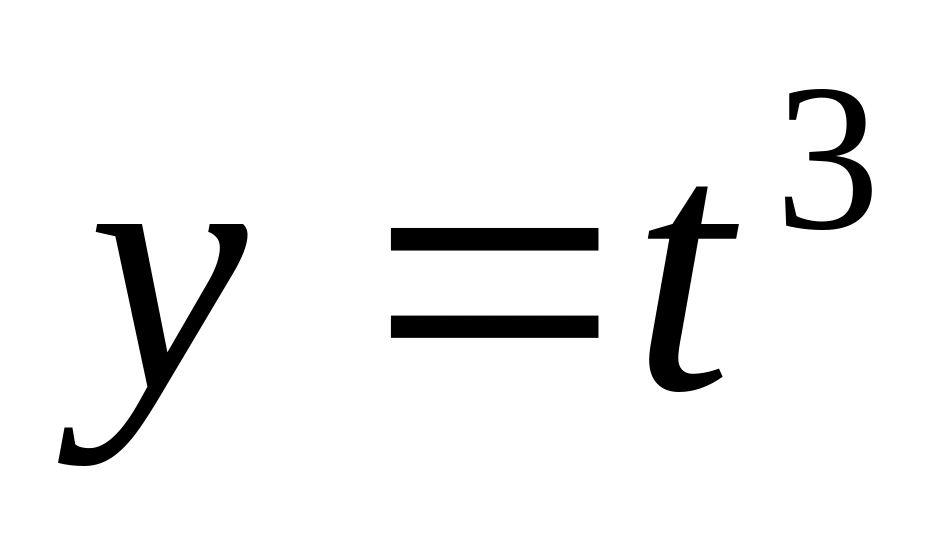 при
при
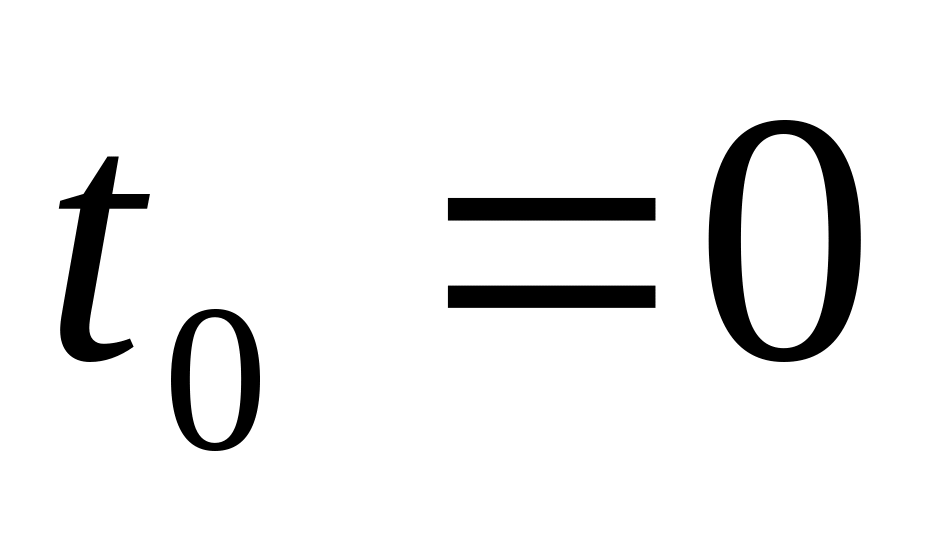
Ответ: а)1 (верный ответ); б) 2; в) -1; г) 0.
Вычислить значение производной сложной функции
 ,
где
,
где
 ,
,
 при
при
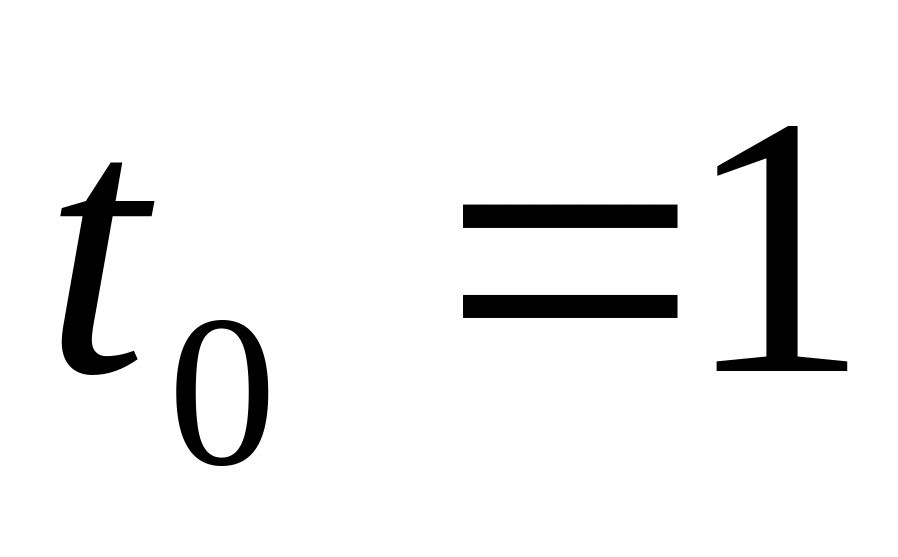
Ответ: а)1; б) 2; в) -1; г) 0 (верный ответ).
Вычислить значение производной сложной функции
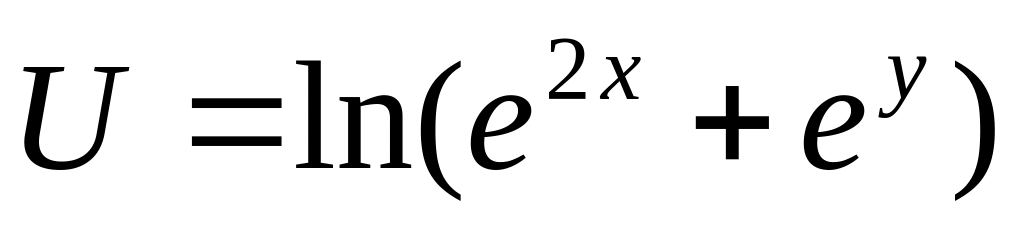 ,
где
,
где
 ,
,
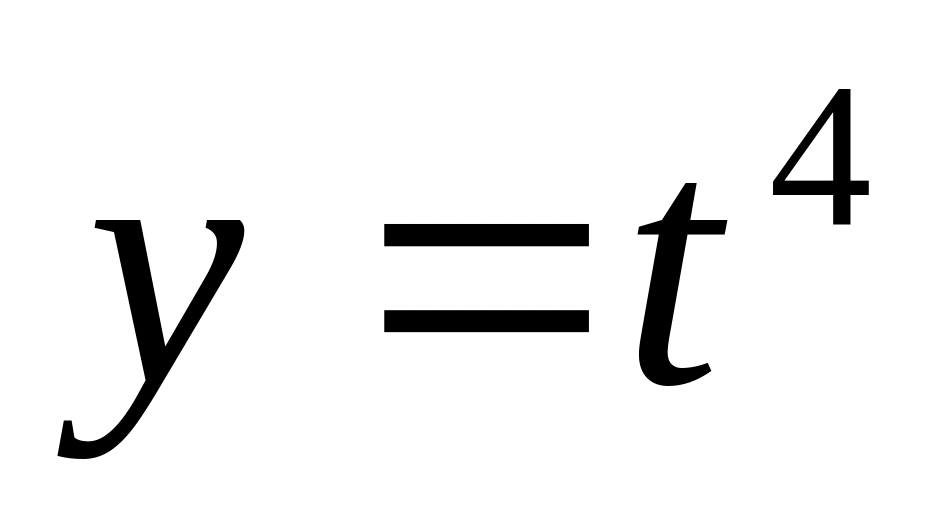 при
при
Ответ: а)1; б) 4(верный ответ); в) -1; г) 5.
Вычислить значение производной сложной функции
 ,
где
,
,
где
,
 при
при
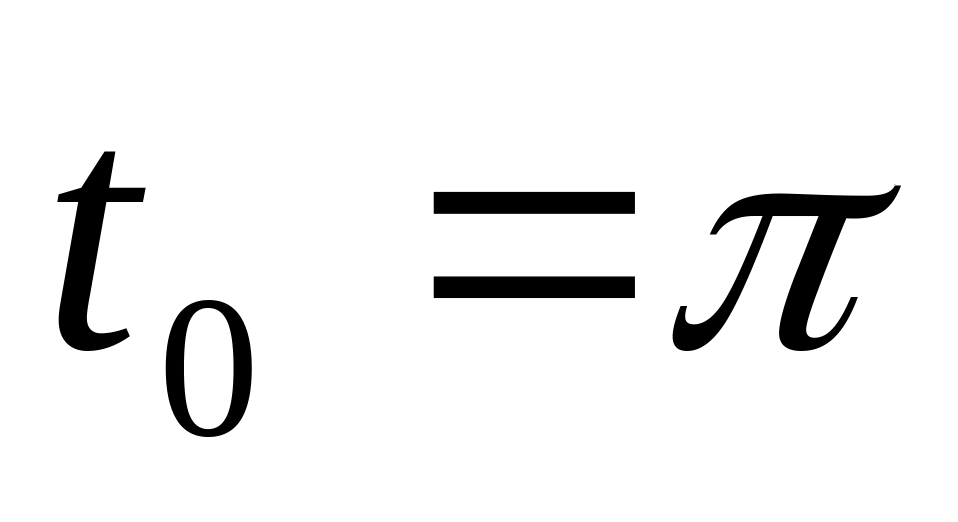
Ответ: а) ; б) 4; в) 2(верный ответ); г) 5.
Вычислить значение производной сложной функции
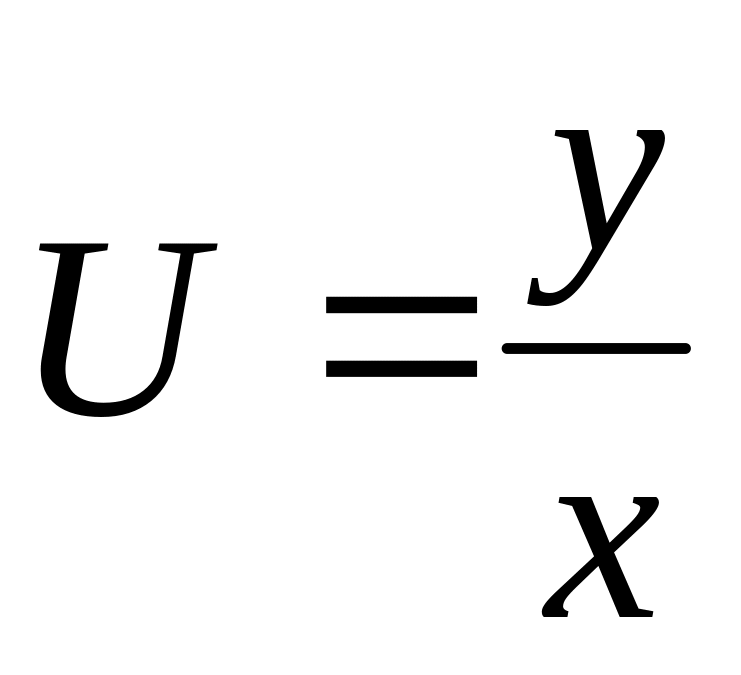 ,
где
,
где
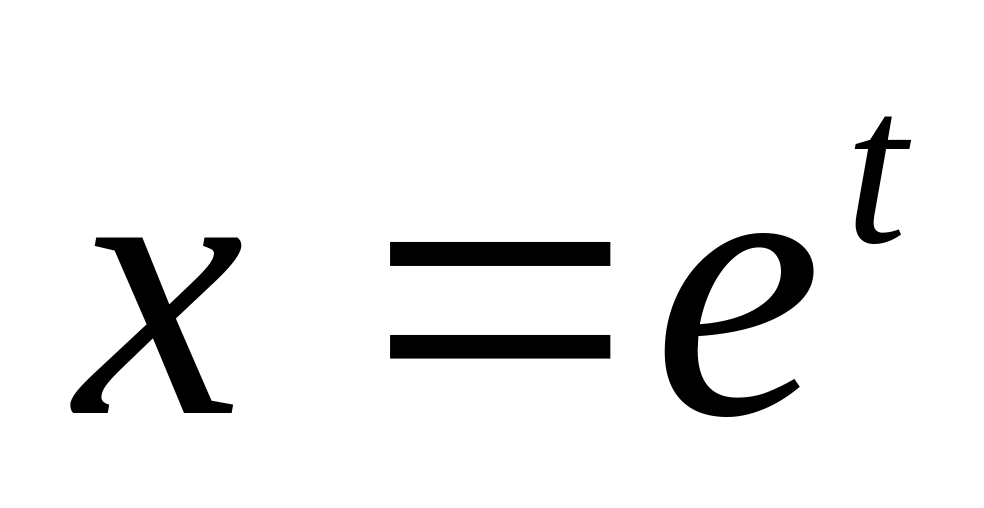 ,
,
 при
при
Ответ: а)
;
б)
-2(верный ответ);
в)
![]() ;
г) 0.
;
г) 0.
Какая из указных функций удовлетворяет указанному уравнению
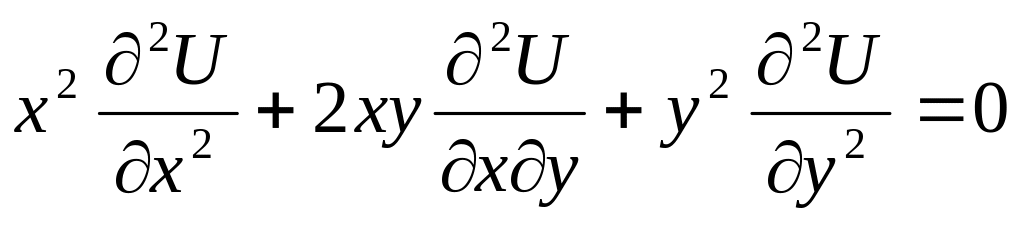
Ответ: а)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Какая из указных функций удовлетворяет указанному уравнению

Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() (верный
ответ);
г)
(верный
ответ);
г)
![]() .
.
Какая из указных функций удовлетворяет указанному уравнению
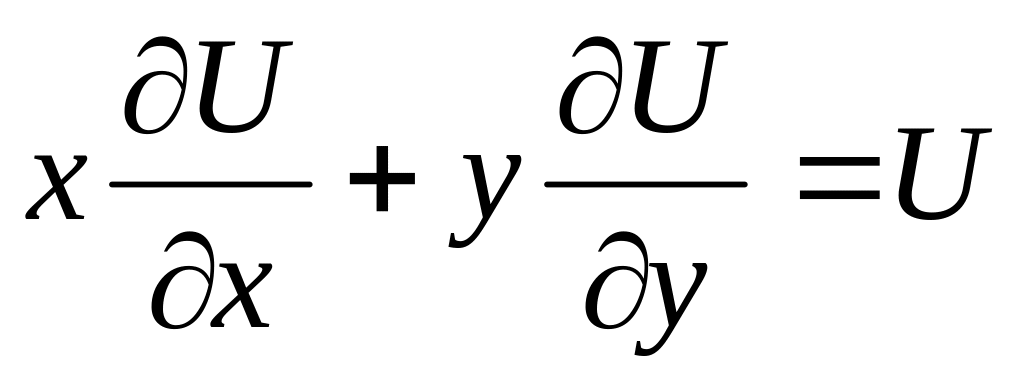
Ответ: а)
![]() ;
б)
;
б)
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Какая из указных функций удовлетворяет указанному уравнению
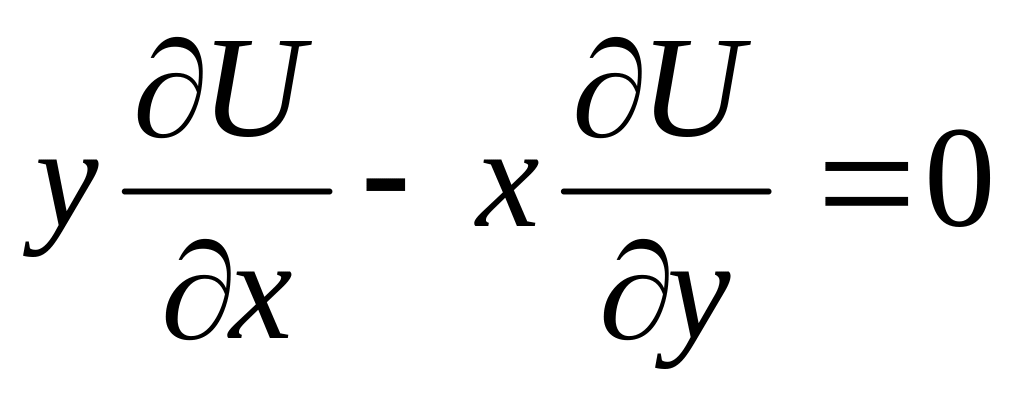
Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Какая из указных функций удовлетворяет указанному уравнению
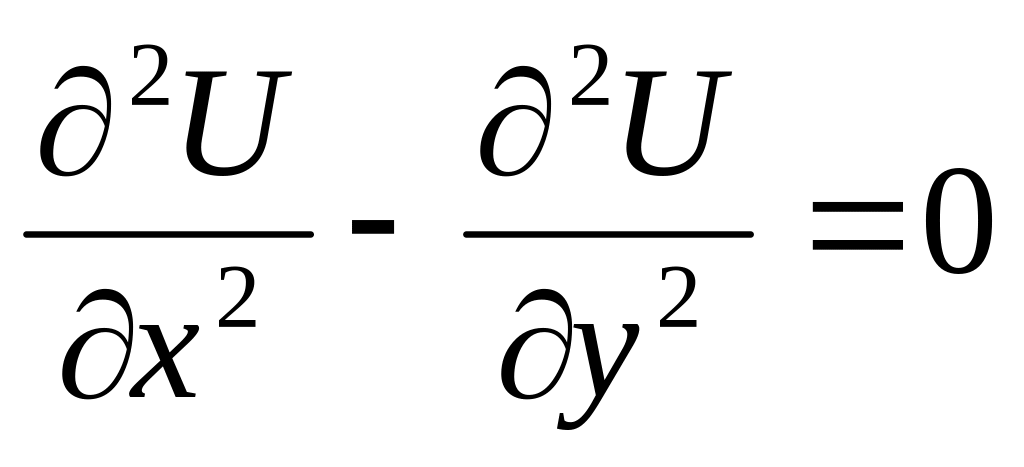
Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
.
;
г)
.
Найти уравнение касательной плоскости к поверхности
 в точке
в точке
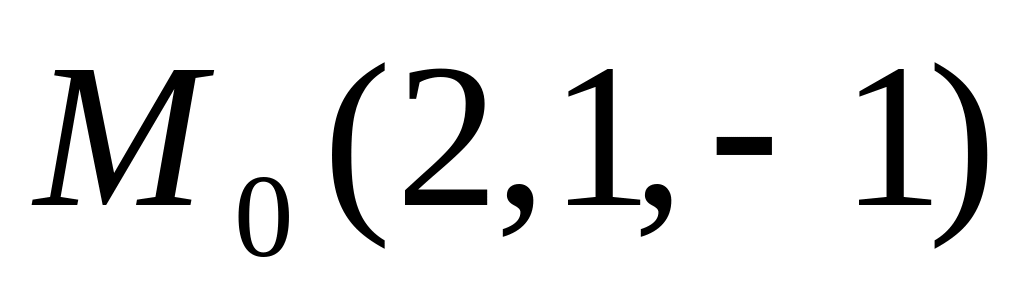
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() (верный
ответ).
(верный
ответ).
Найти уравнение касательной плоскости к поверхности
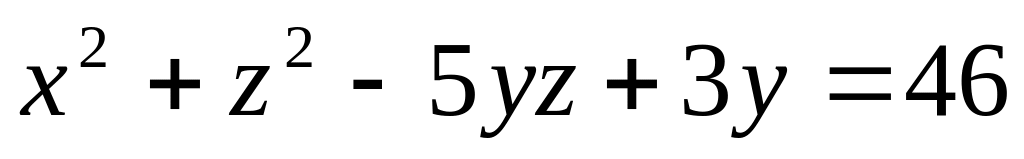 в точке
в точке

Ответ: а)
![]() ;
б)
;
б)
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Найти уравнение касательной плоскости к поверхности
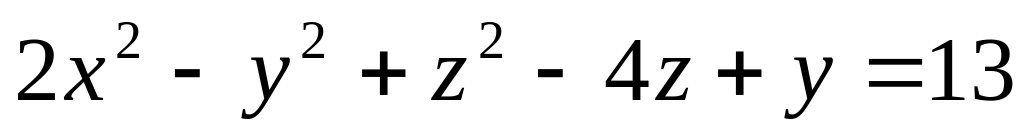 в точке
в точке
Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() (верный
ответ);
г)
(верный
ответ);
г)
![]() .
.
Найти уравнения нормали к поверхности
 в точке
в точке

Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Найти уравнения нормали к поверхности
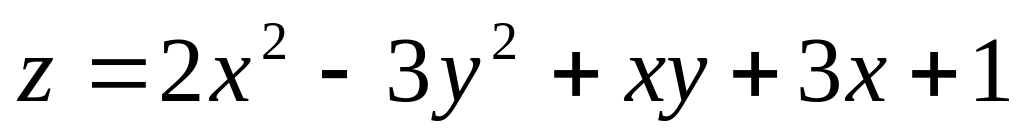 в точке
в точке

Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() (верный
ответ).
(верный
ответ).
Записать уравнение касательной плоскости к поверхности
 в точке
в точке

Ответ: а)
![]() ;
б)
;
б)
![]() (верный ответ);
в)
(верный ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Записать уравнение нормали к плоскости
 в точке
в точке
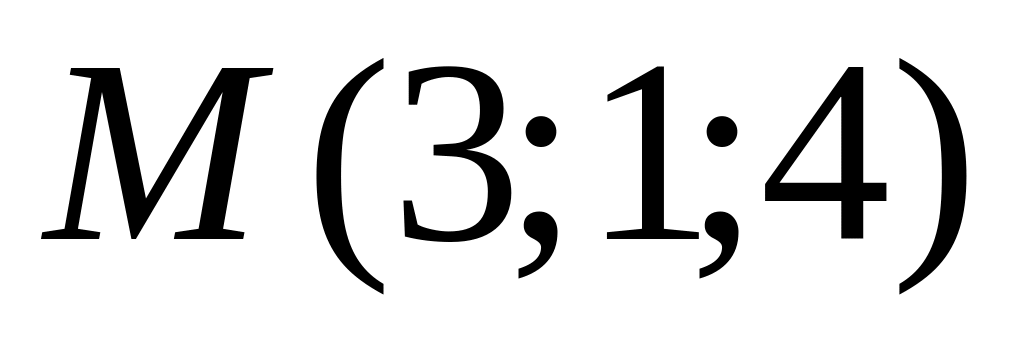
Ответ: а)
![]() ;
б)
;
б)
![]() (верный ответ);
в)
(верный ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Исследовать на экстремум следующую функцию
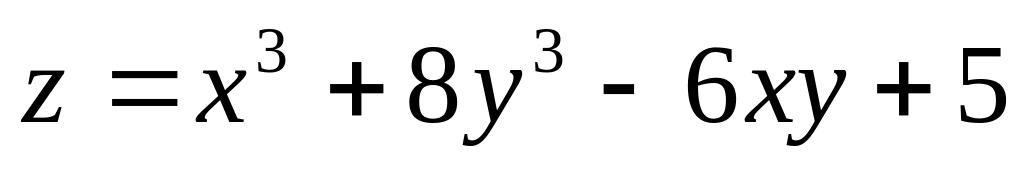
Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Исследовать на экстремум следующую функцию
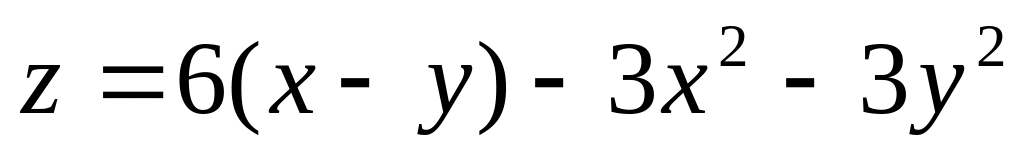
Ответ: а)
![]() ;
б)
;
б)
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ;
г)
;
г)
![]() .
.
Исследовать на экстремум следующую функцию

Ответ: а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() (верный
ответ).
(верный
ответ).
Исследовать на экстремум следующую функцию

Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Исследовать на экстремум следующую функцию
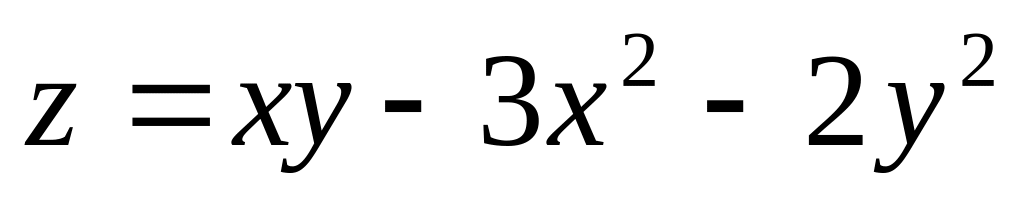
Ответ: а)
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Ряды
Если числовой ряд
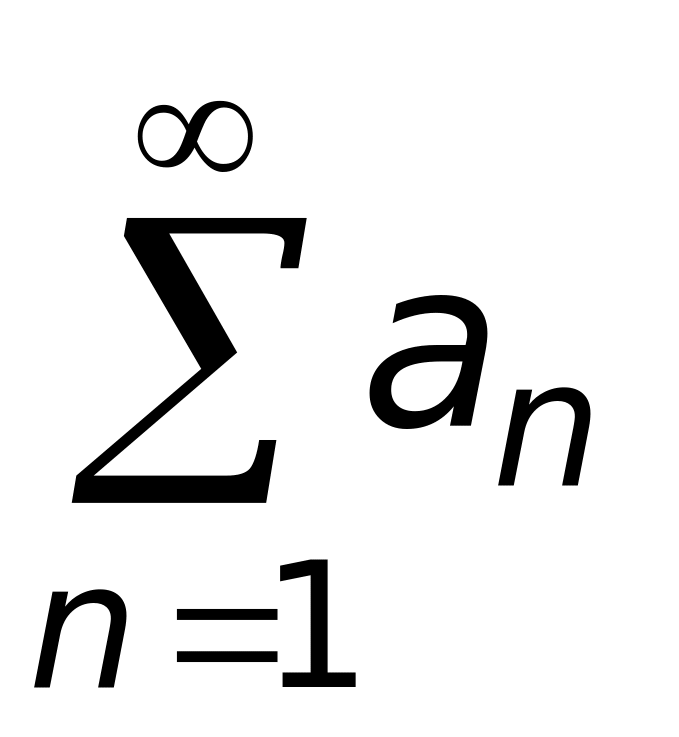 сходится, то его общий член
сходится, то его общий член
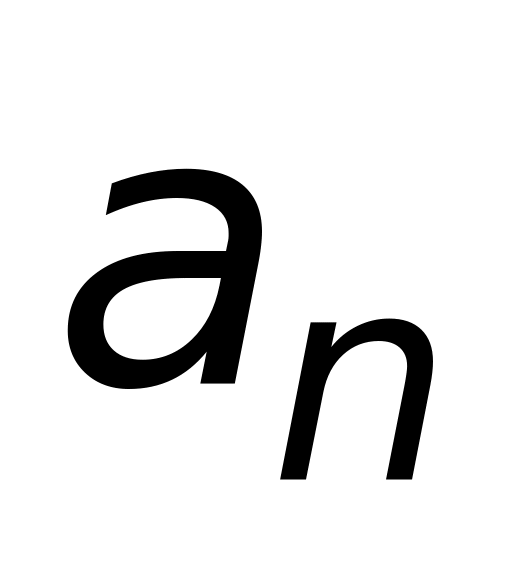 при
при
 стремится к:
1) 1;
2) –1;
3) 0 (верный
ответ);
4) 1/2.
стремится к:
1) 1;
2) –1;
3) 0 (верный
ответ);
4) 1/2.Если числовой ряд сходится, т.е.
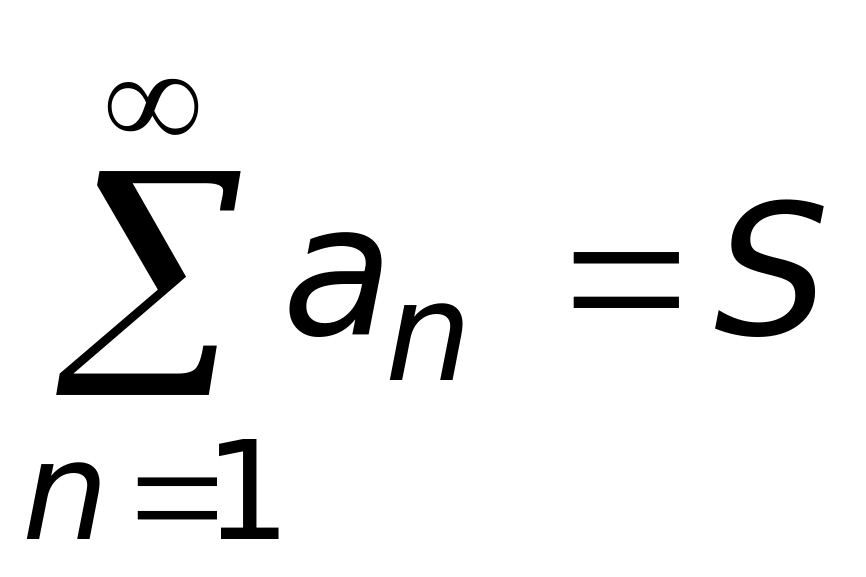 ,
то последовательность его частичных
сумм
,
то последовательность его частичных
сумм
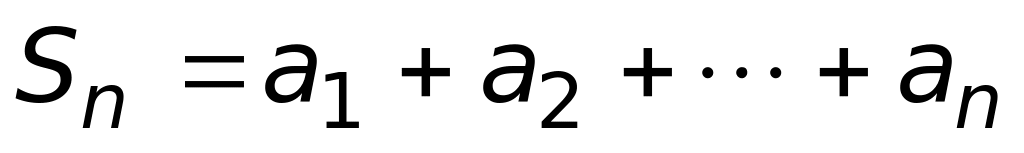 ,
сходится к:
1) 2S;
2) S
(верный ответ);
3) ½S;
4) +
,
сходится к:
1) 2S;
2) S
(верный ответ);
3) ½S;
4) + .
.Если , то ряд
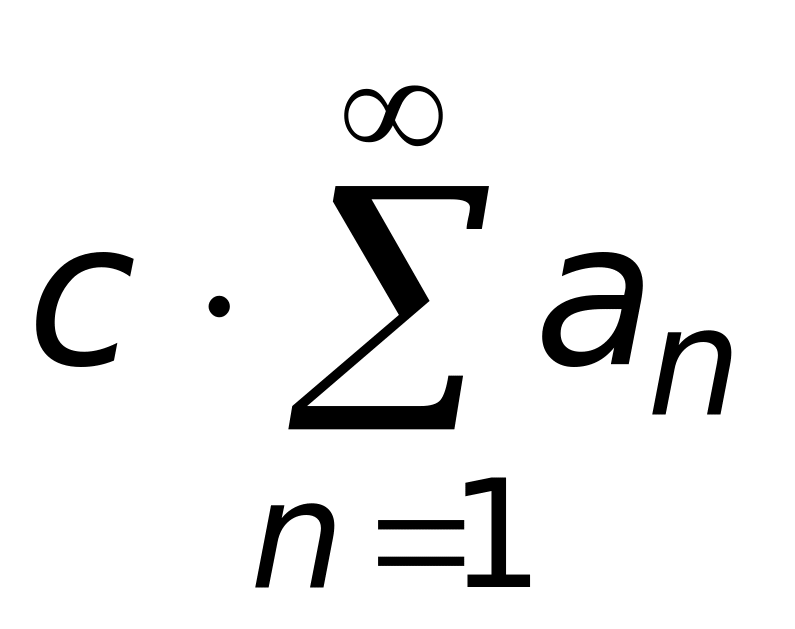 сходится к:
1)
сходится к:
1)
 ;
2)
;
2)
 (верный ответ);
3) 3S;
4) +
.
(верный ответ);
3) 3S;
4) +
.Гармонический ряд
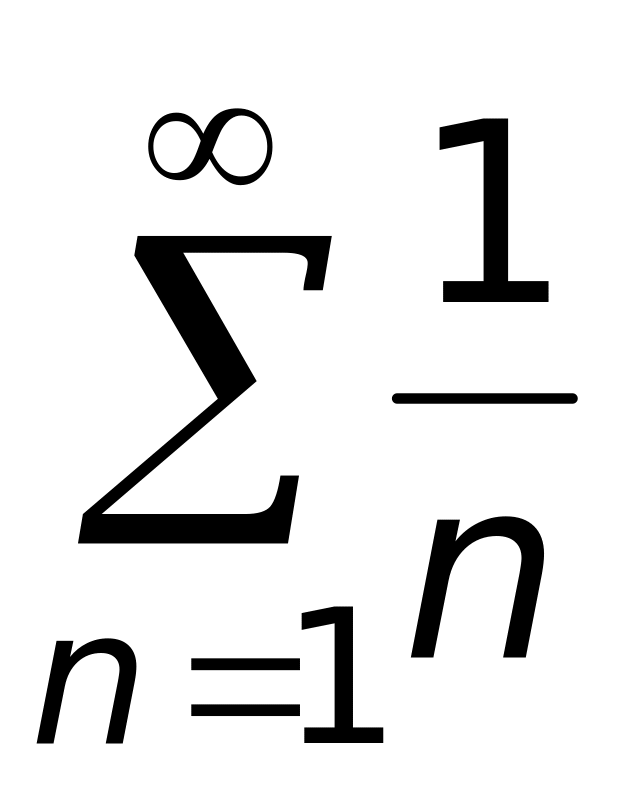 имеет сумму равную:
1) 1;
2) +
(верный ответ);
3) ½;
4) 5.
имеет сумму равную:
1) 1;
2) +
(верный ответ);
3) ½;
4) 5.Если
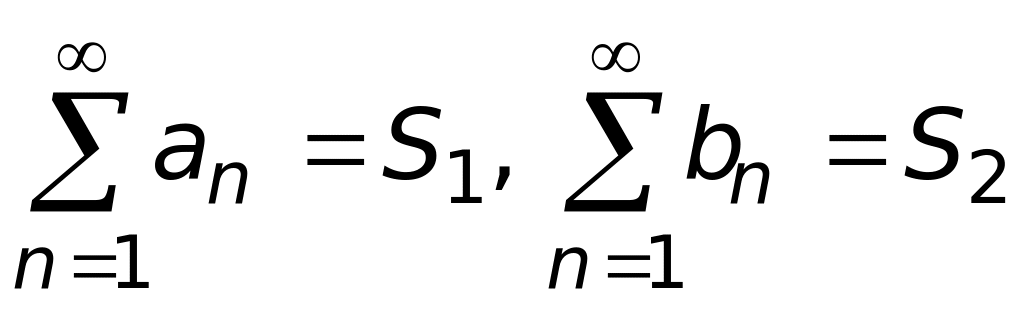 ,
то ряд
,
то ряд
 сходится к:
1)
сходится к:
1)
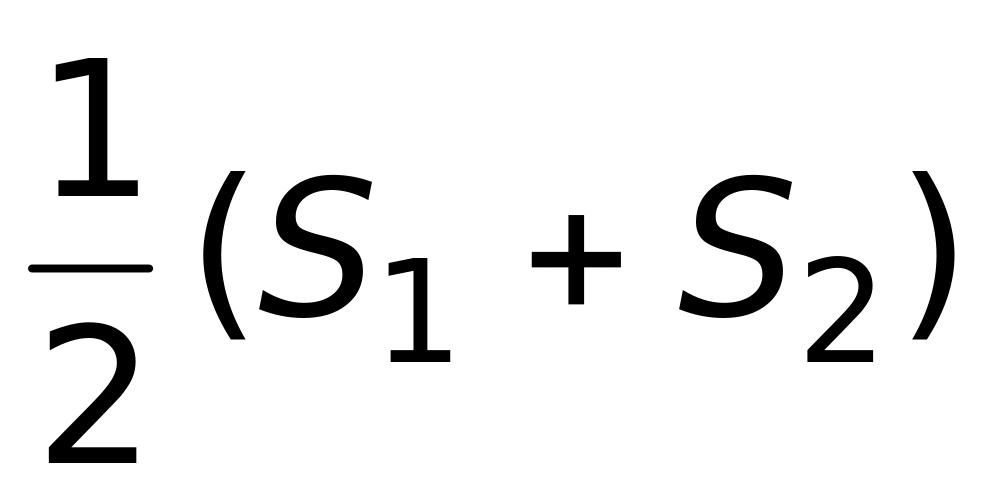 ;
2)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
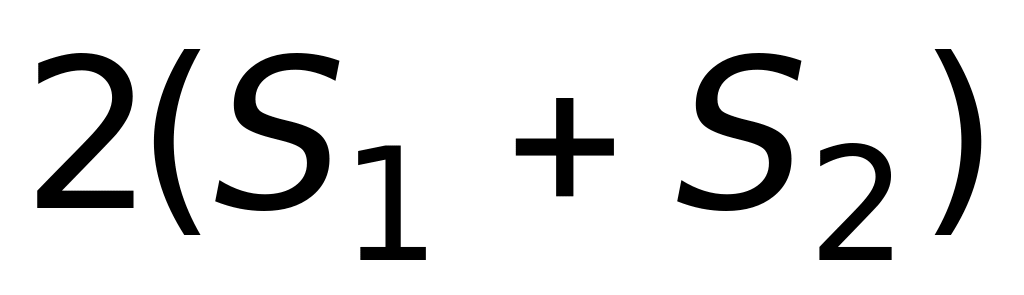 ;
4) +
.
;
4) +
.Числовой ряд
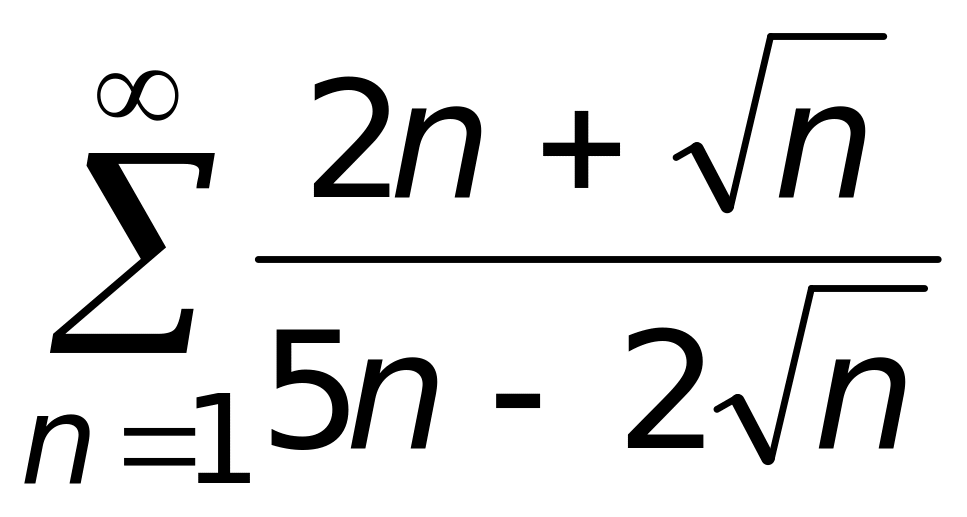 1) сходится;
2) расходится (верный
ответ);
3) сходится условно;
4)
сходится равномерно.
1) сходится;
2) расходится (верный
ответ);
3) сходится условно;
4)
сходится равномерно.Числовой ряд
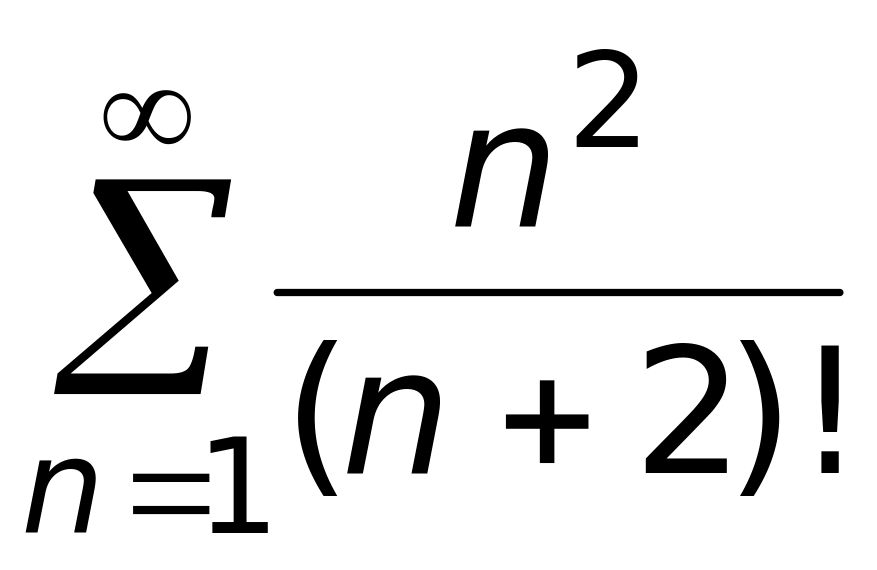 1) сходится (верный ответ);
2)
сходится условно;
3) расходится;
4)
сходится равномерно.
1) сходится (верный ответ);
2)
сходится условно;
3) расходится;
4)
сходится равномерно.Числовой ряд
 1) расходится;
2) сходится условно;
3) сходится (верный ответ);
4)
сходится равномерно.
1) расходится;
2) сходится условно;
3) сходится (верный ответ);
4)
сходится равномерно.Числовой ряд
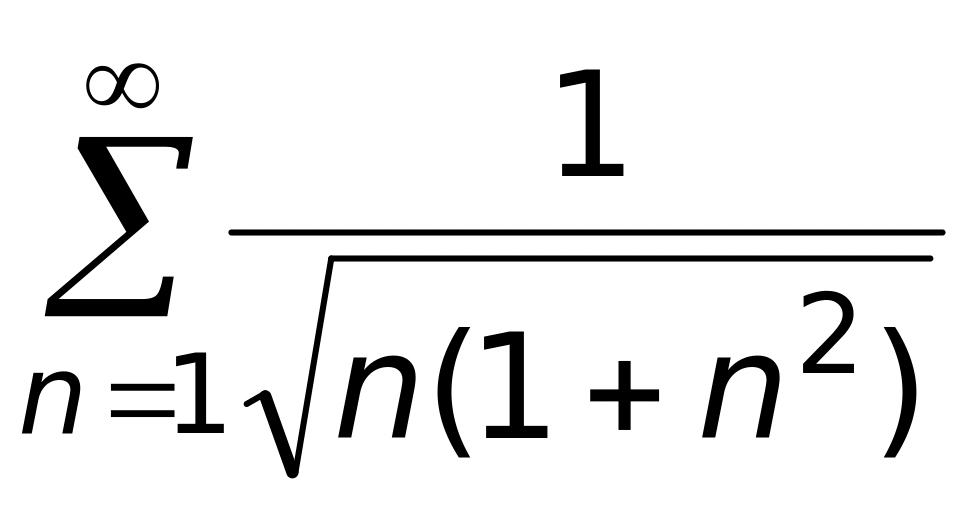 1) сходится условно;
2) расходится;
3) сходится (верный ответ);
4)
сходится равномерно.
1) сходится условно;
2) расходится;
3) сходится (верный ответ);
4)
сходится равномерно.Числовой ряд
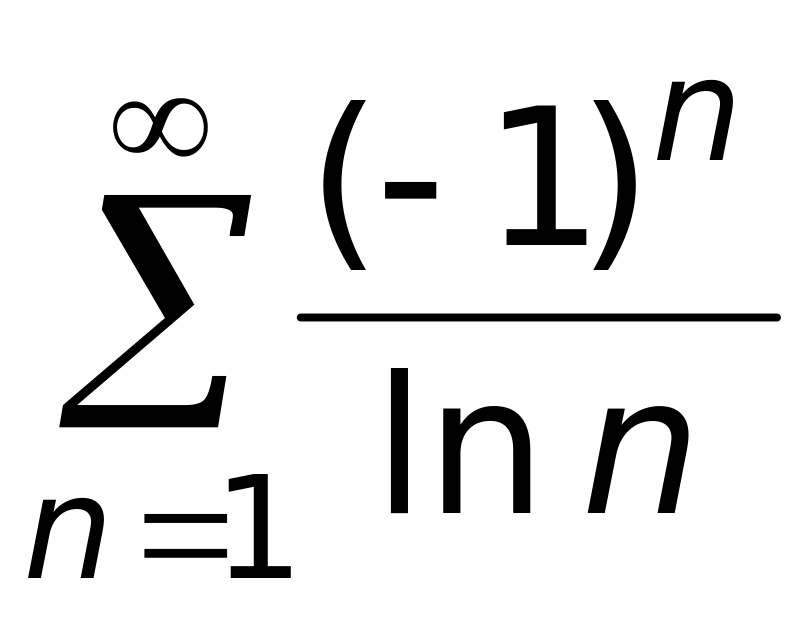 1)расходится;
2) сходится абсолютно;
3) сходится условно (верный ответ);
4) сходится равномерно.
1)расходится;
2) сходится абсолютно;
3) сходится условно (верный ответ);
4) сходится равномерно.Числовой ряд
 1) сходится (верный ответ);
2)
расходится;
3) сходится условно;
4)
сходится равномерно.
1) сходится (верный ответ);
2)
расходится;
3) сходится условно;
4)
сходится равномерно.Степенной ряд
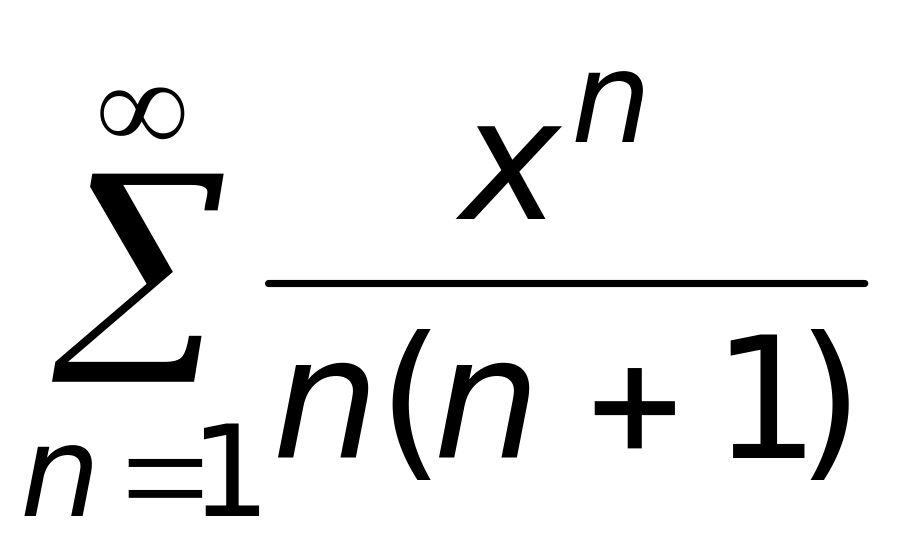 1) сходится на промежутке (2, +
);
2) сходится на отрезке [-1, 1] (верный
ответ);
3) сходится на интервале (3,
4);
4) сходится на промежутке (-
,
0).
1) сходится на промежутке (2, +
);
2) сходится на отрезке [-1, 1] (верный
ответ);
3) сходится на интервале (3,
4);
4) сходится на промежутке (-
,
0).Степенной ряд
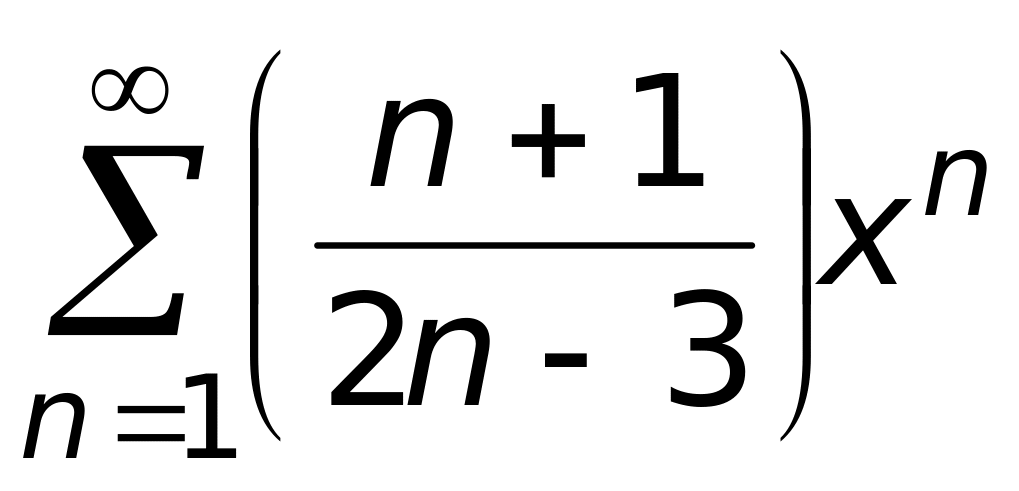 1) сходится в интервале (-3, -2);
2)
сходится на промежутке [2, +
);
3) сходится в интервале (-1, 1) (верный
ответ);
4) сходится на промежутке
(-
,
-4].
1) сходится в интервале (-3, -2);
2)
сходится на промежутке [2, +
);
3) сходится в интервале (-1, 1) (верный
ответ);
4) сходится на промежутке
(-
,
-4].Интервал сходимости степенного ряда
 равен
1) (1, 3) (верный ответ);
2) (0,
1);
3) (-1, 0);
4) (3, 4).
равен
1) (1, 3) (верный ответ);
2) (0,
1);
3) (-1, 0);
4) (3, 4).Интервал сходимости степенного ряда
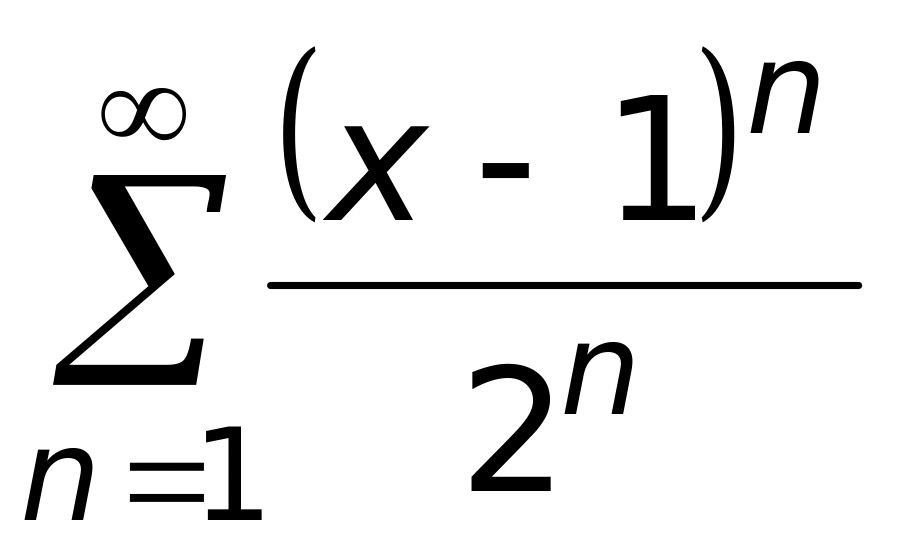 равен
1) (-1, 3) (верный ответ);
2) (3,
4);
3) (-2, -1);
4) (5, 6).
равен
1) (-1, 3) (верный ответ);
2) (3,
4);
3) (-2, -1);
4) (5, 6).Сумма степенного ряда
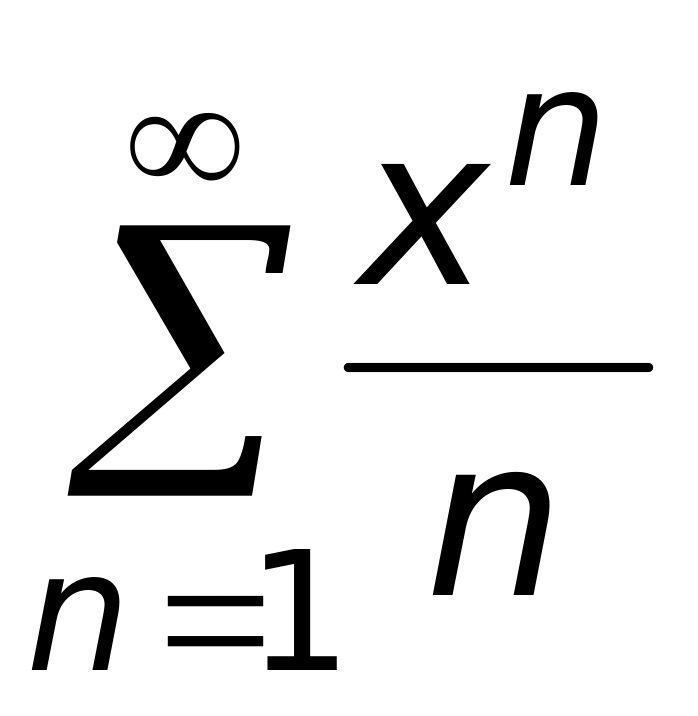 равна
1)
равна
1)
 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
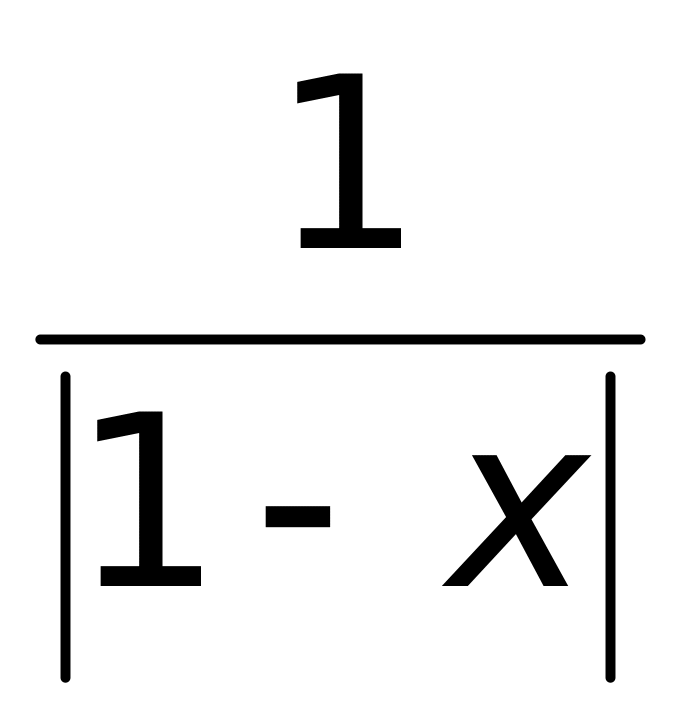 ;
4)
;
4)
 .
.Сумма степенного ряда
 равна
1)
равна
1)
 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
4)
;
3)
;
4)
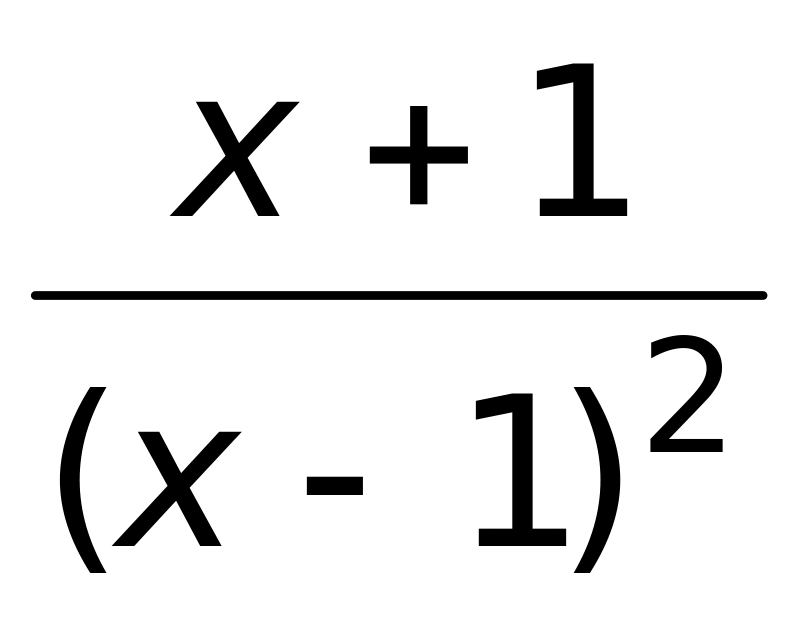 .
.Сумма степенного ряда
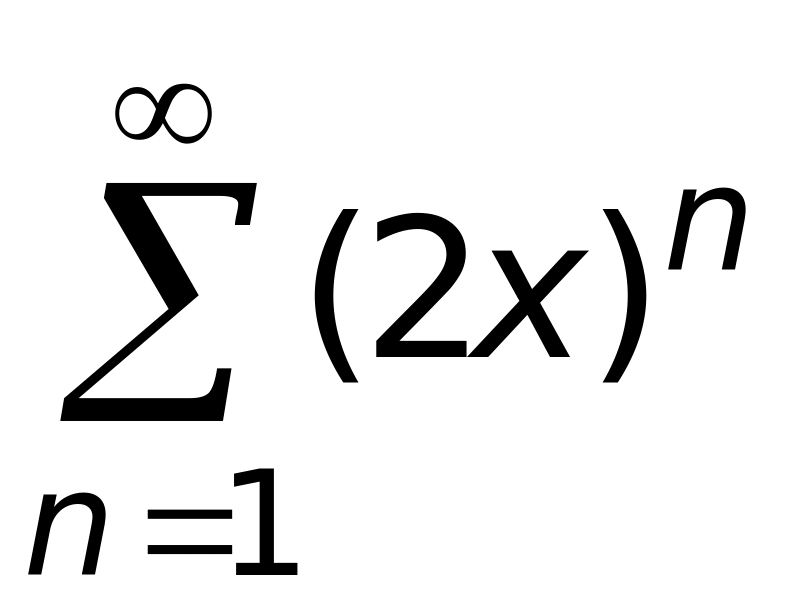 равна
1)
равна
1)
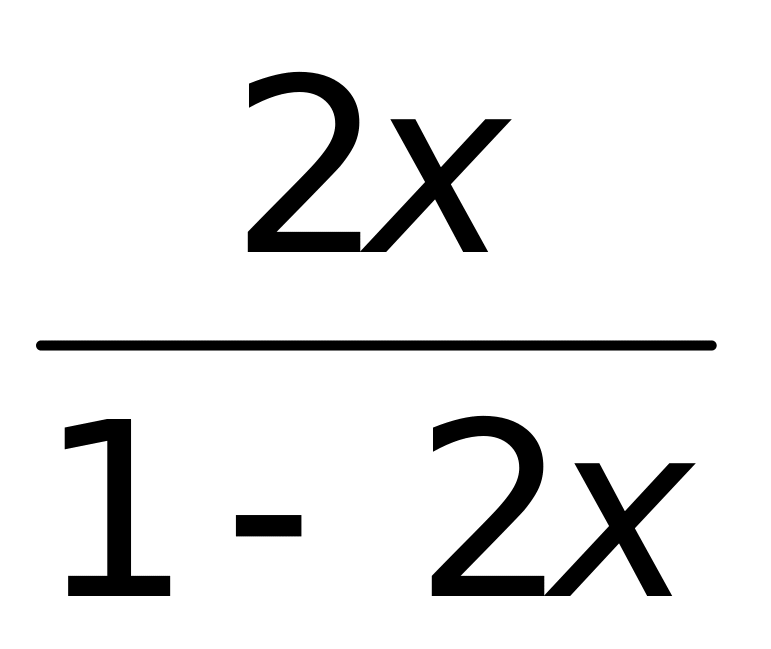 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
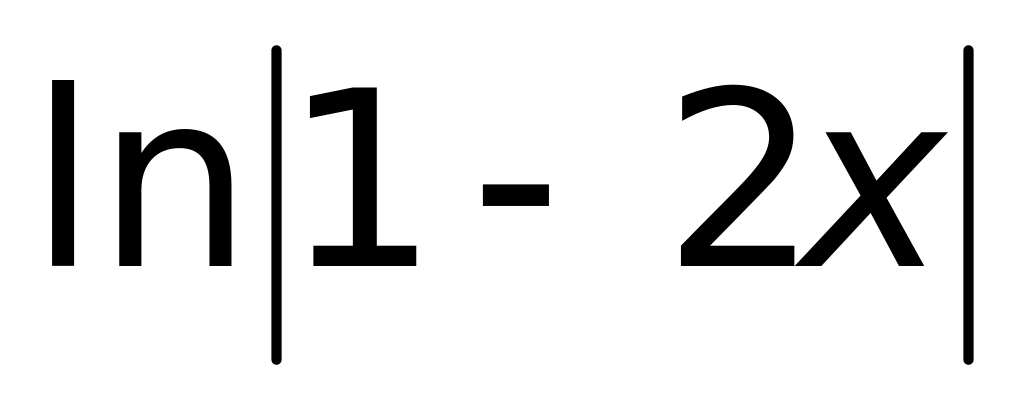 ;
4)
;
4)
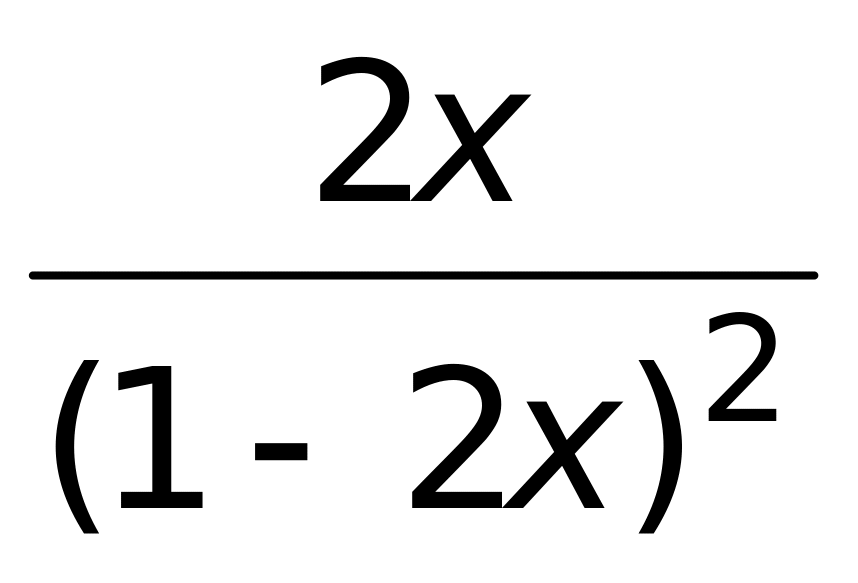 .
.Производная суммы функционального ряда
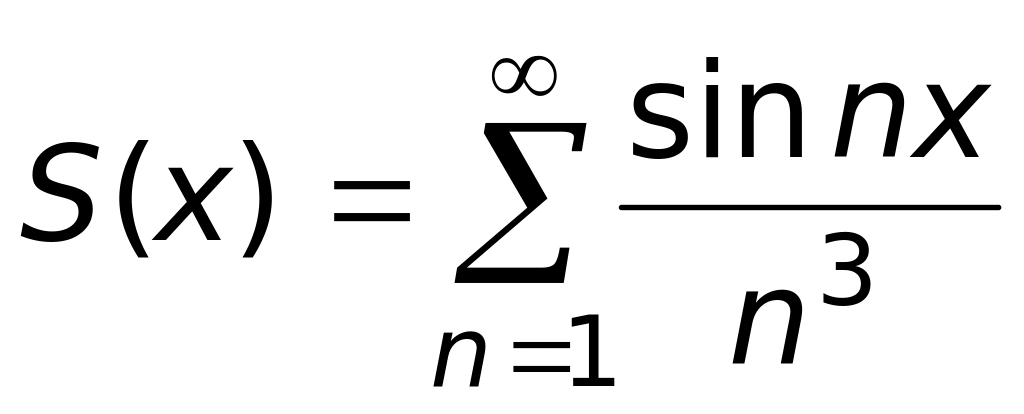 равна
1)
равна
1)
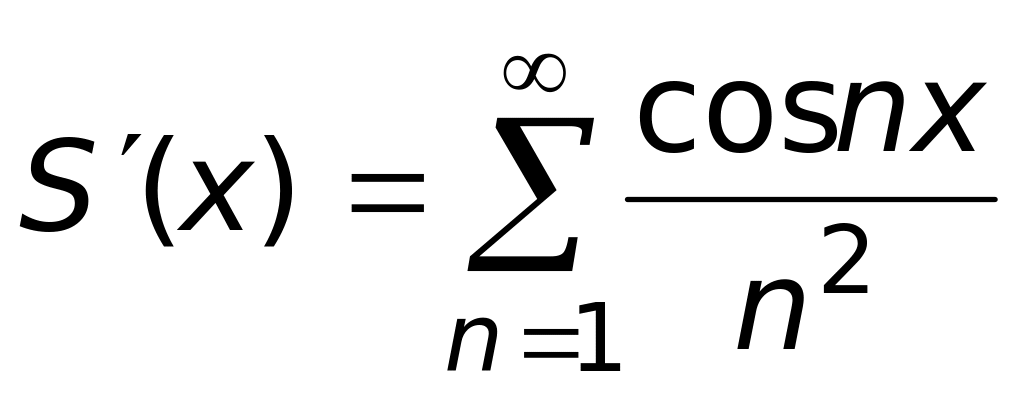 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
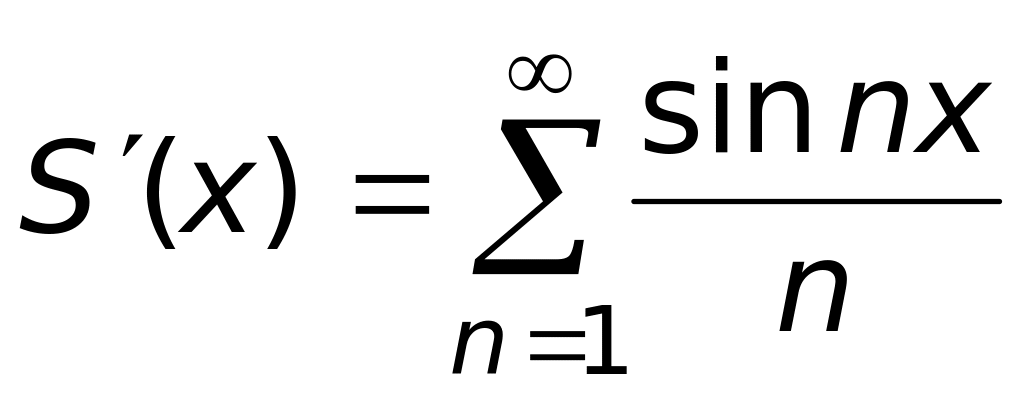 ;
4)
;
4)
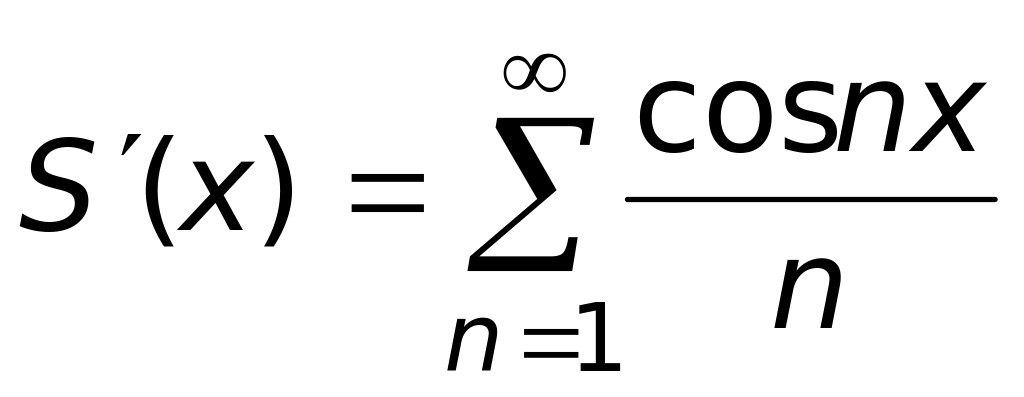 .
.Производная суммы функционального ряда
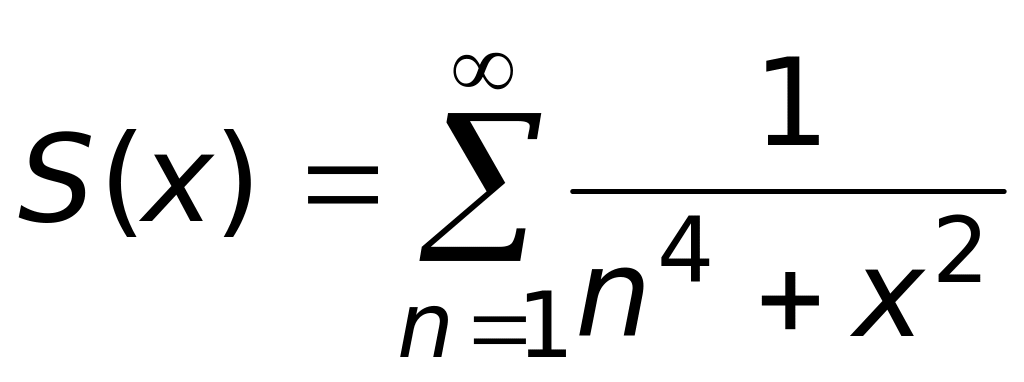 равна
1)
равна
1)
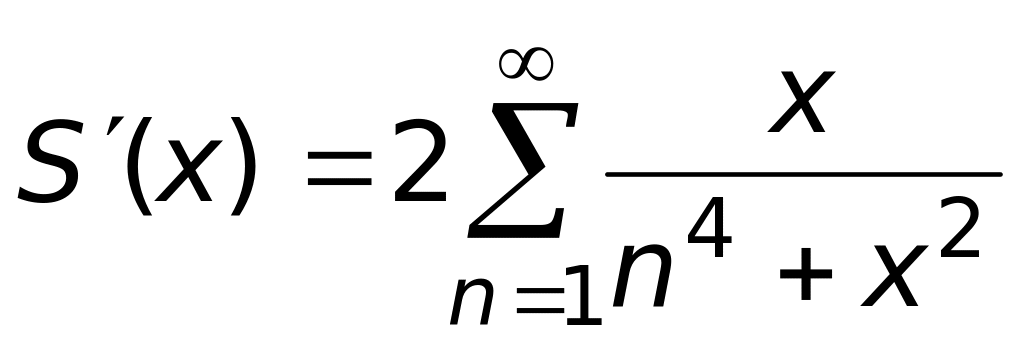 ;
2)
;
2)
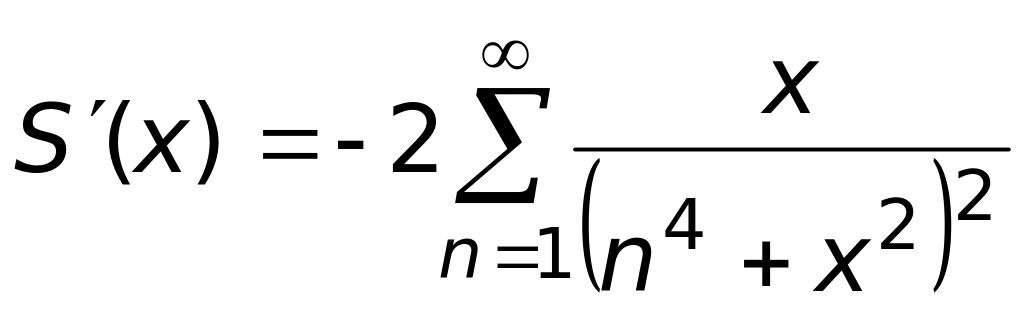 (верный ответ);
3)
(верный ответ);
3)
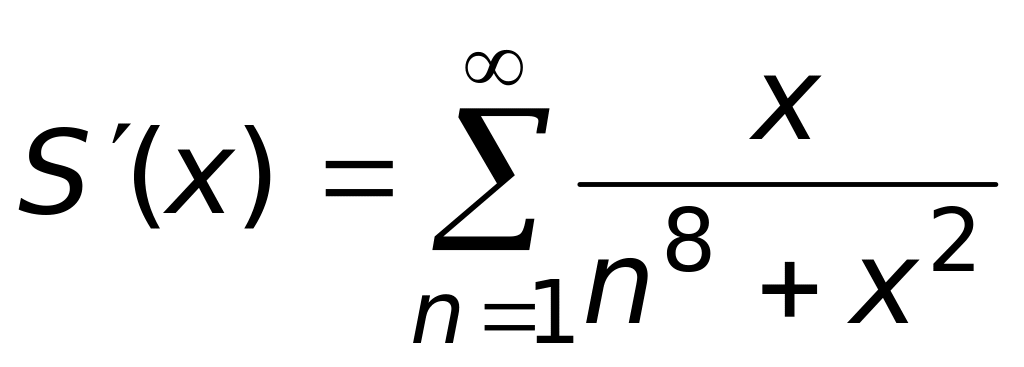 ;
4)
;
4)
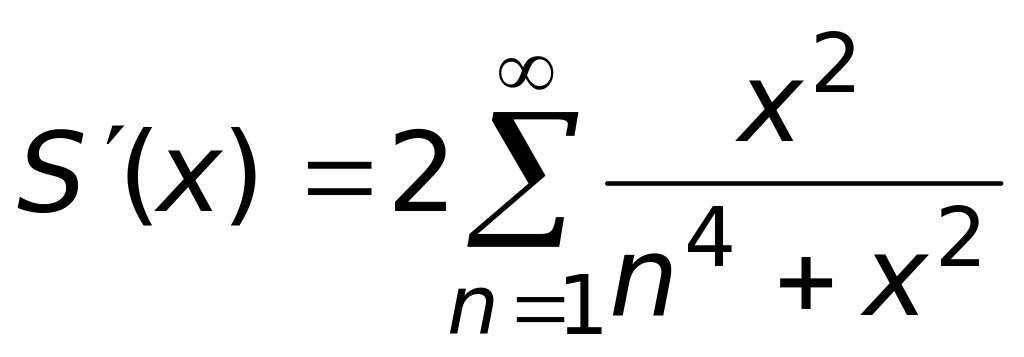 .
.Функциональный ряд
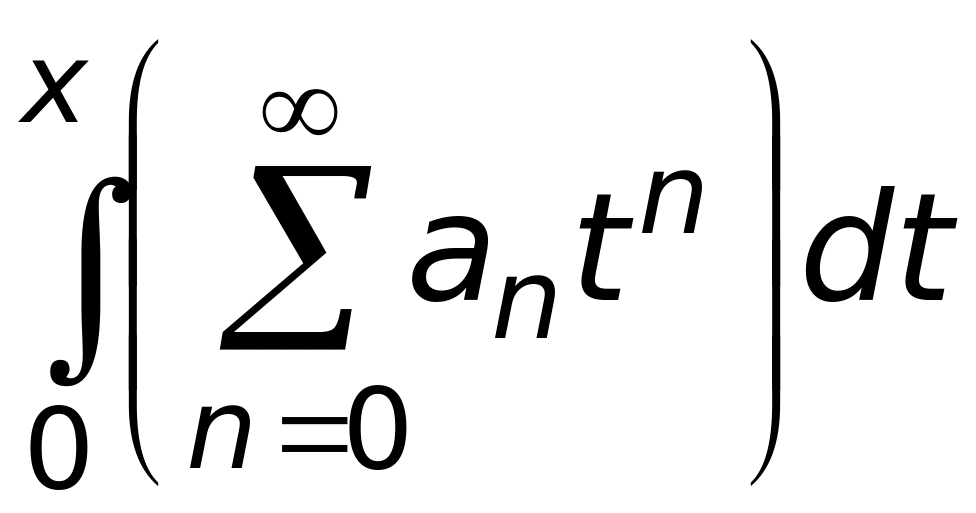 имеет вид:
1)
имеет вид:
1)
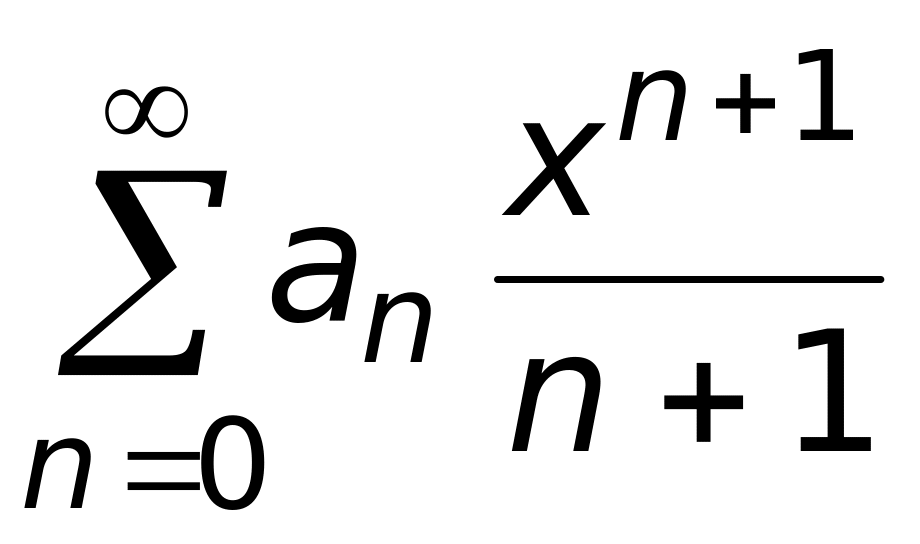 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
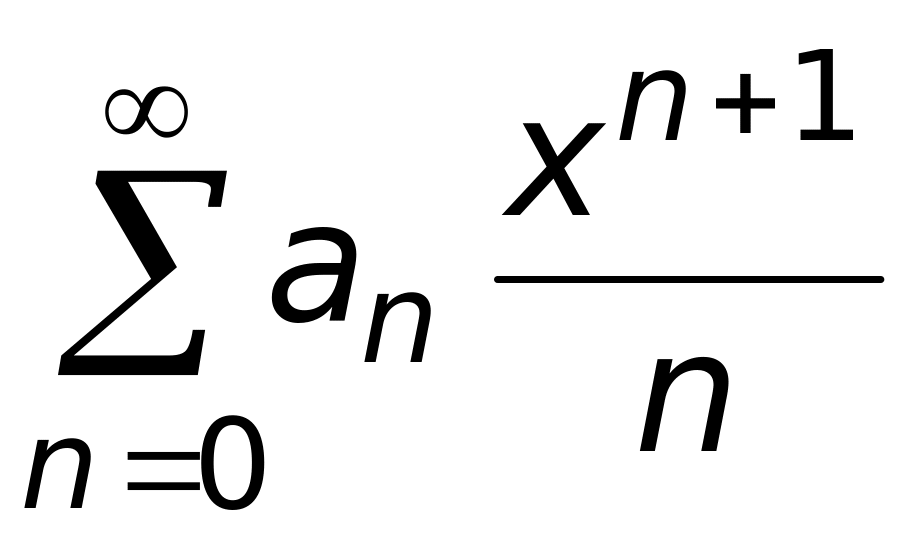 ;
4)
;
4)
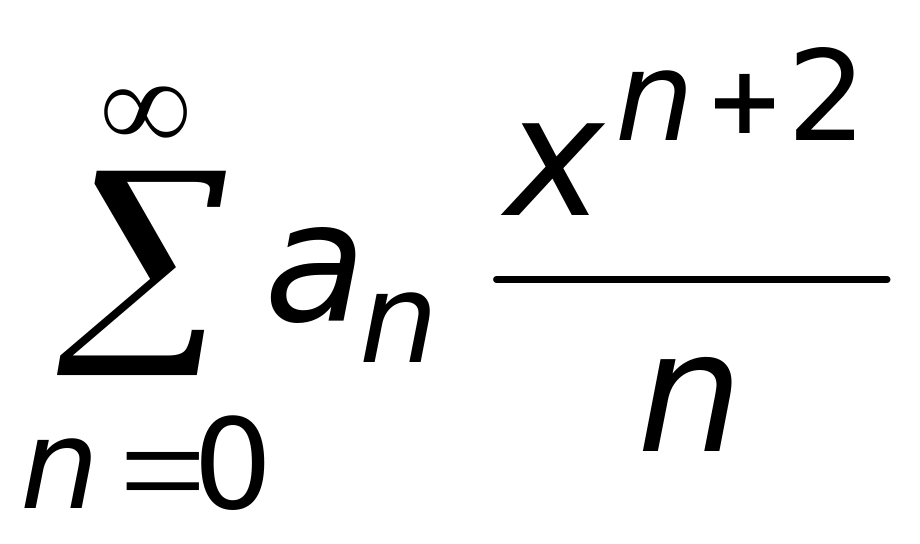 .
.Функциональный ряд
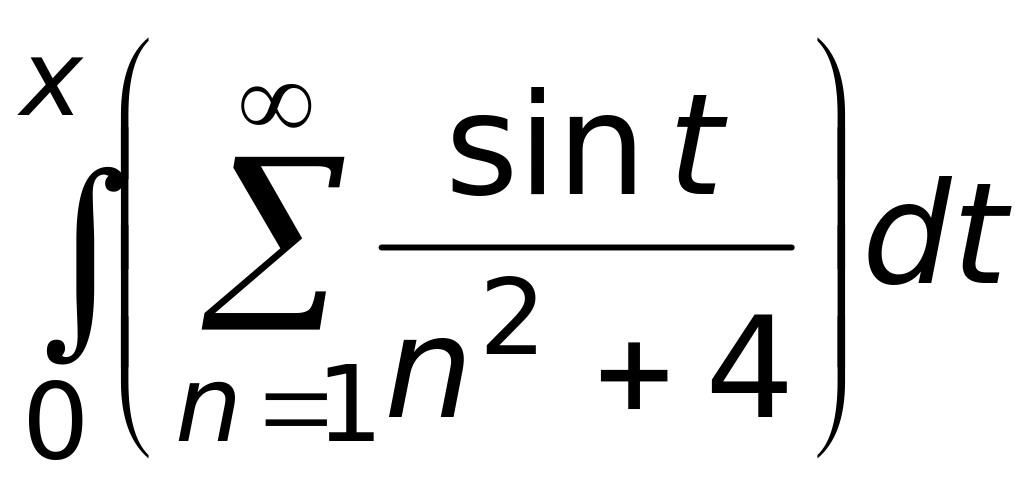 имеет вид:
1)
имеет вид:
1)
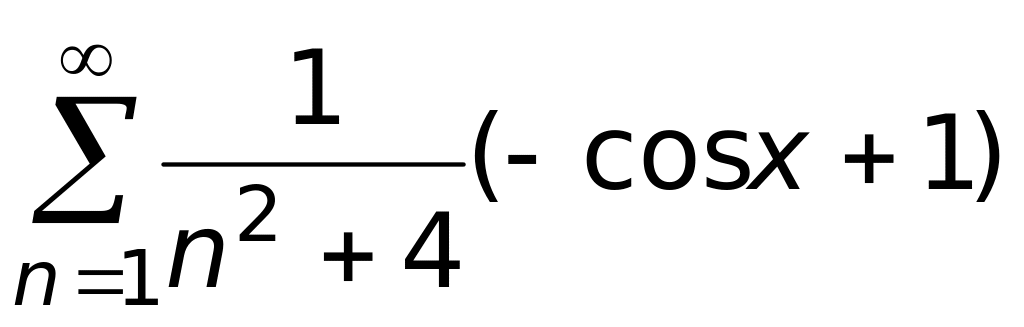 (верный ответ);
2)
(верный ответ);
2)
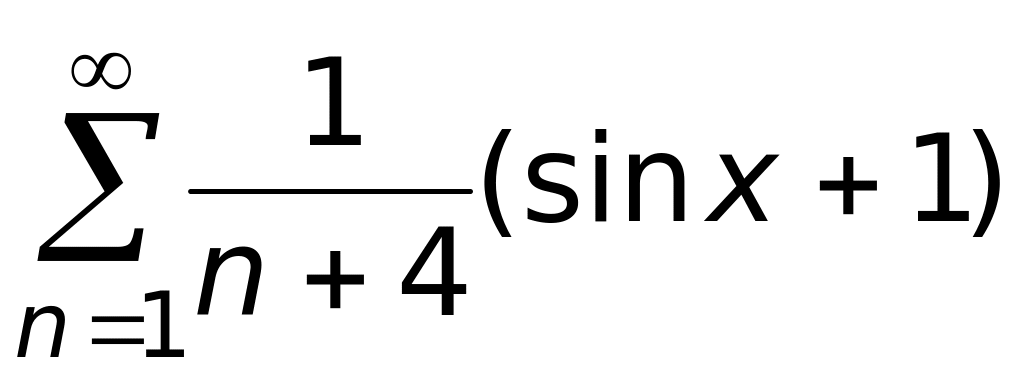 ;
3)
;
3)
 ;
4)
;
4)
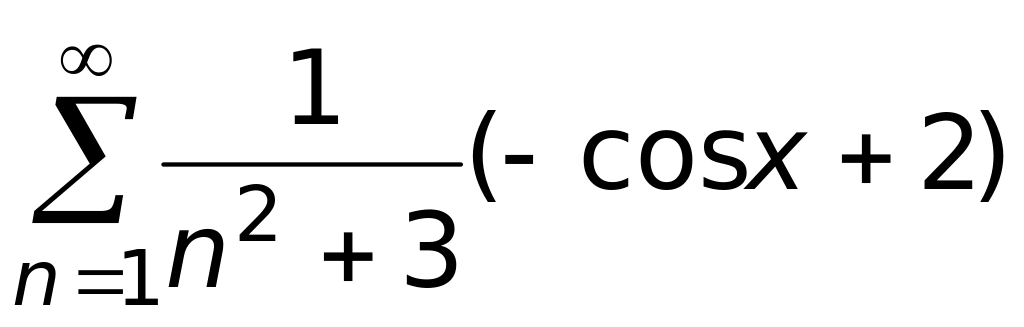 .
.Какой ряд является мажорантным на R для ряда
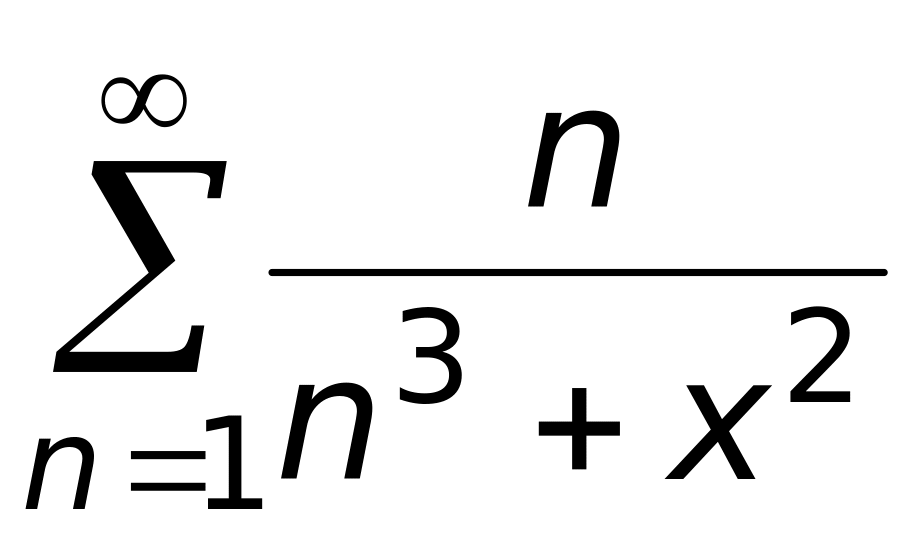 1)
1)
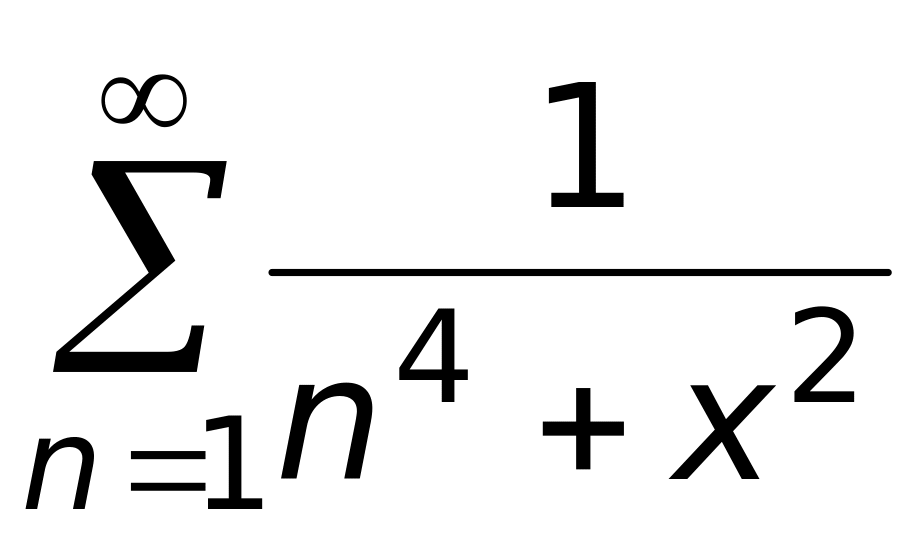 ;
2)
;
2)
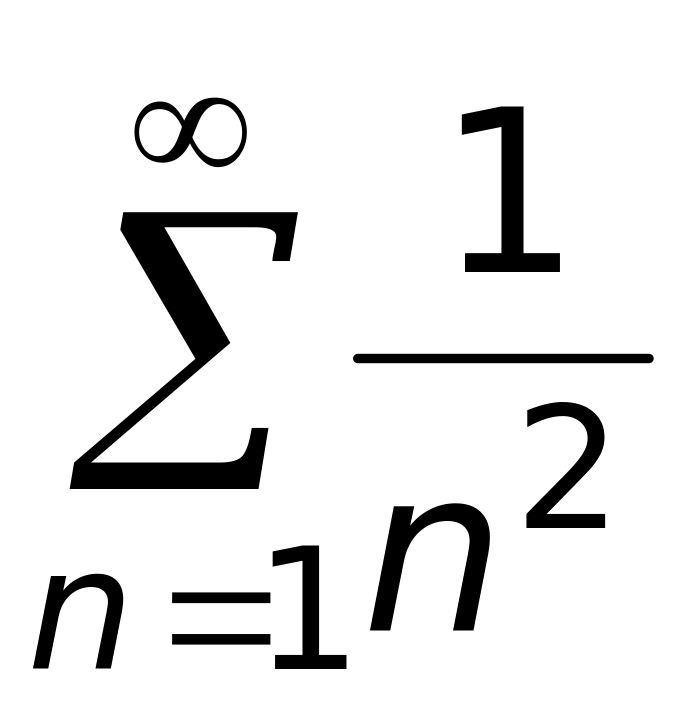 (верный ответ);
3)
(верный ответ);
3)
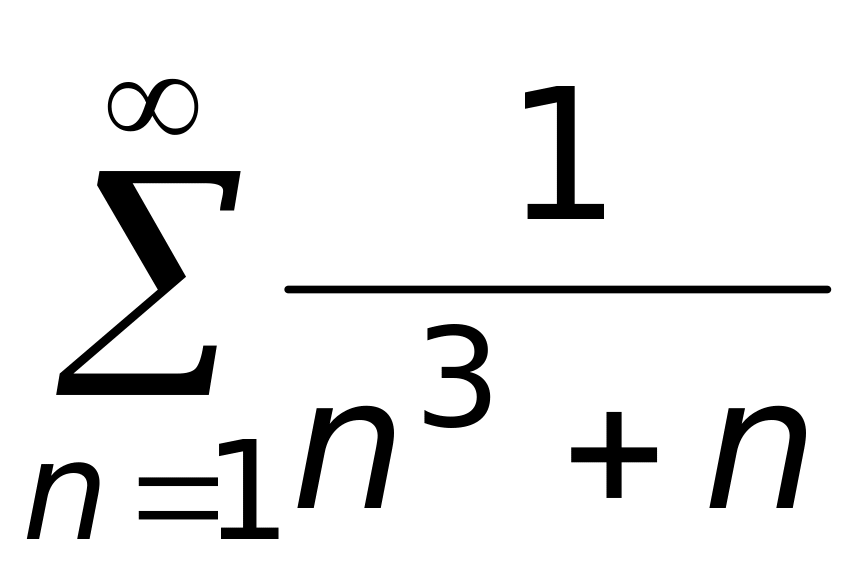 ;
4)
;
4)
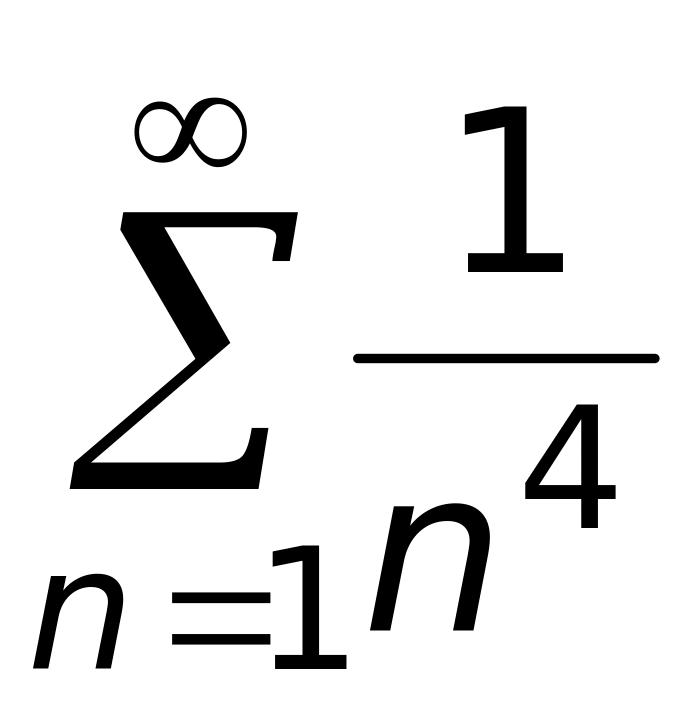 .
.Какой ряд является мажорантным на R для ряда
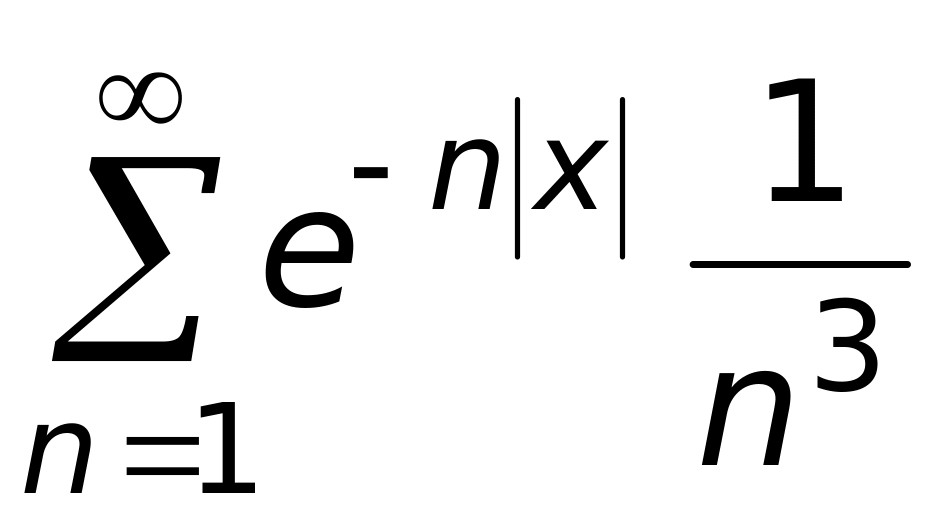 1)
;
2)
1)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
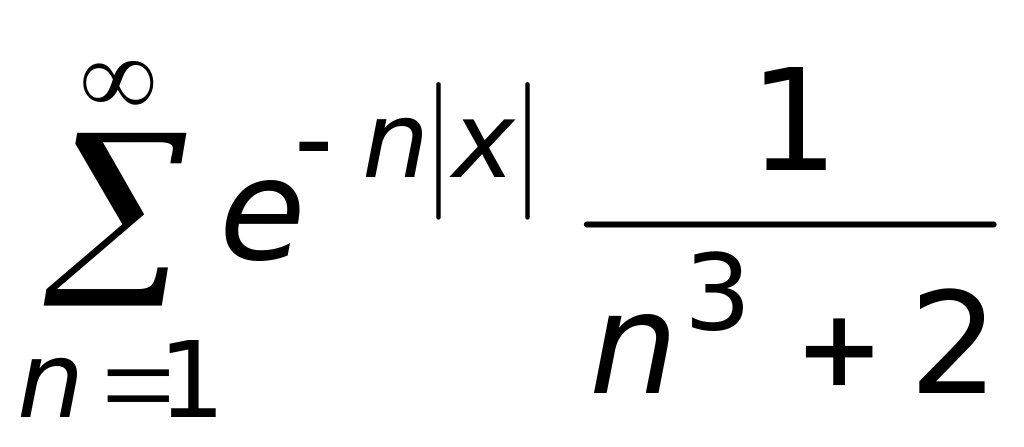 ;
4)
.
;
4)
.Коэффициенты ряда Тейлора в точке для функции равны 1)
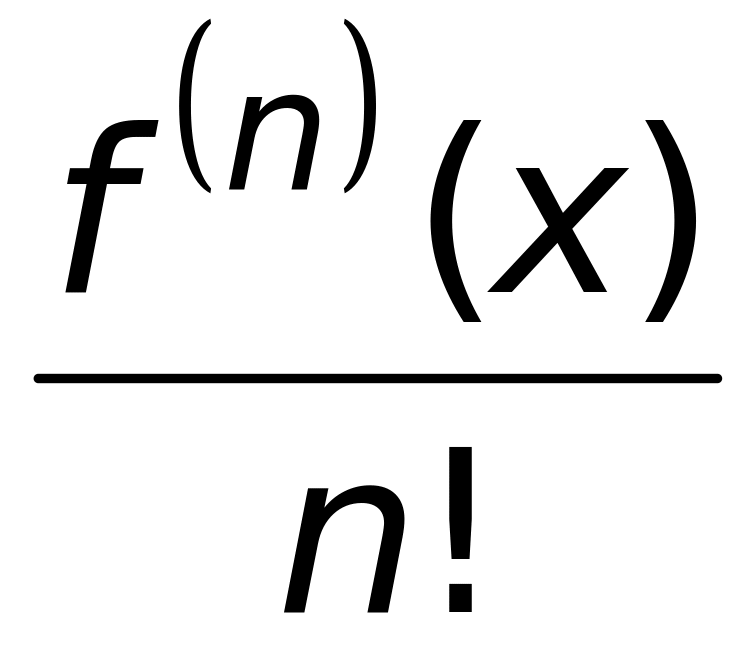 ;
2)
;
2)
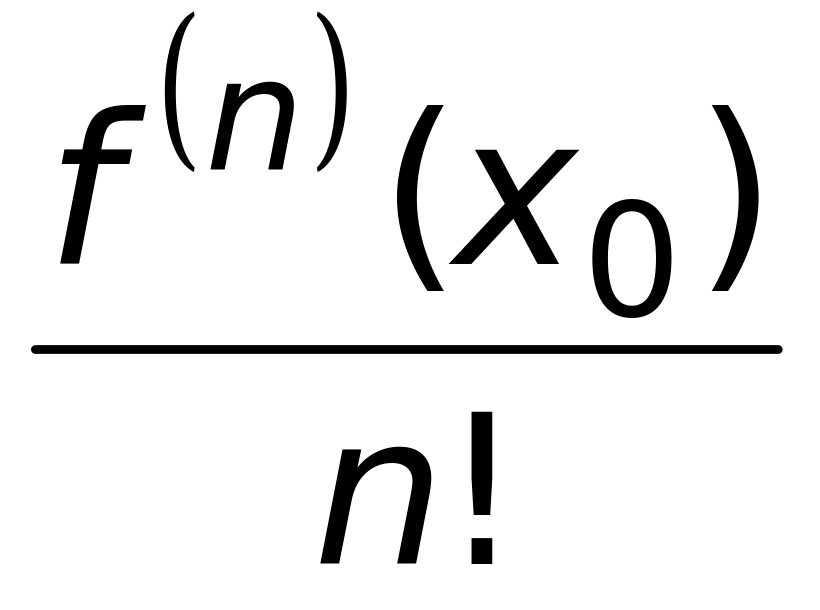 (верный ответ);
3)
(верный ответ);
3)
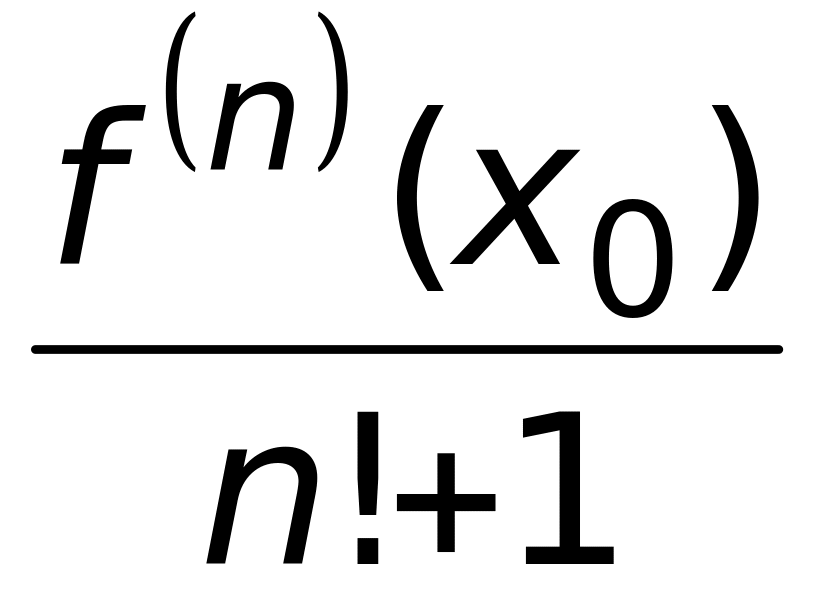 ;
4)
;
4)
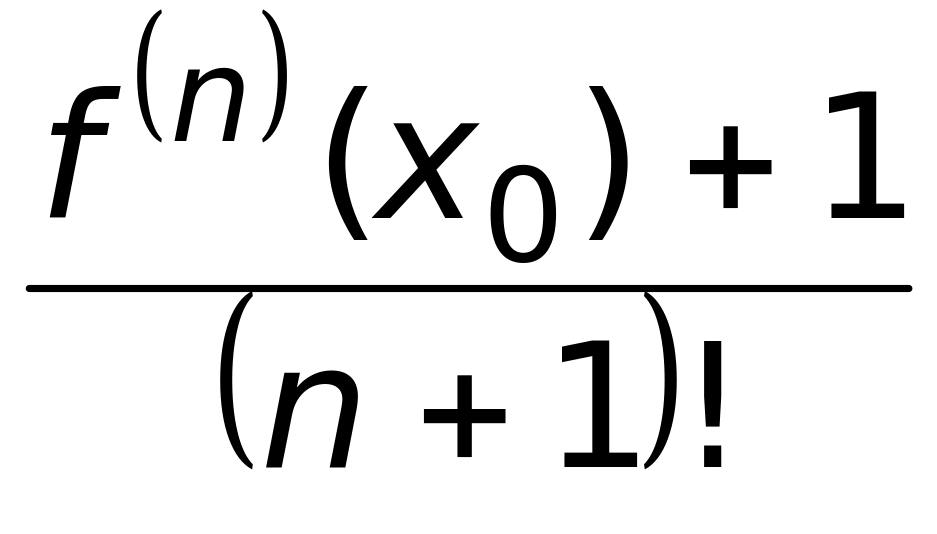 .
.
