
Приложения производной
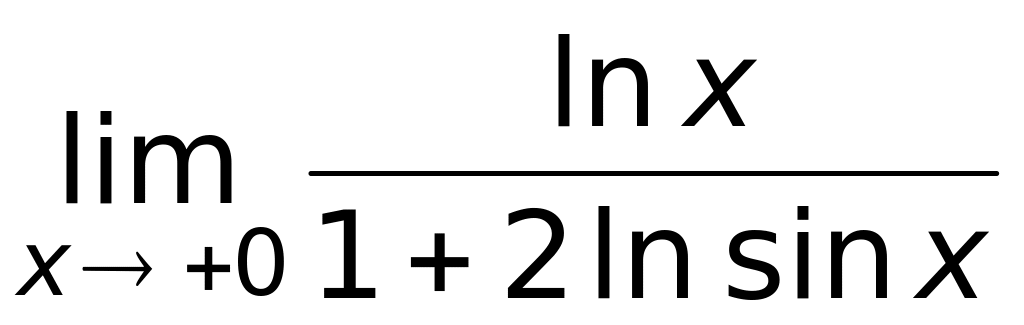 равен:
Ответ:
1) 1;
2)
(верный ответ);
3) 0;
4)
равен:
Ответ:
1) 1;
2)
(верный ответ);
3) 0;
4)
 .
. равен:
Ответ:
1) 4;
2)
равен:
Ответ:
1) 4;
2)
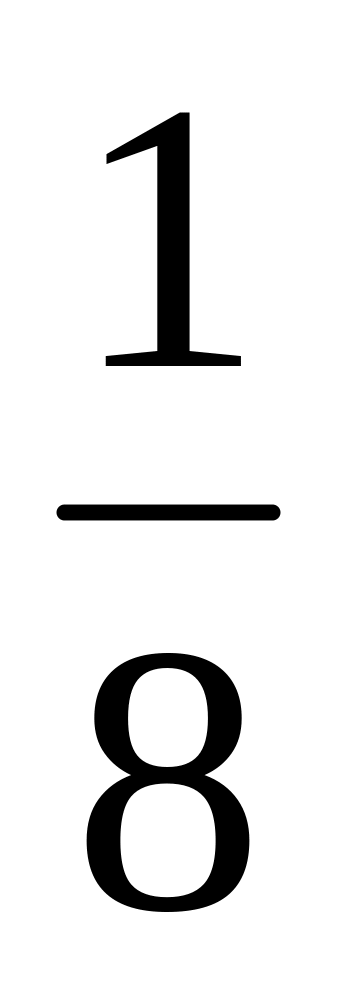 ;
3)
;
3)
 (верный
ответ);
4)
(верный
ответ);
4)
 .
.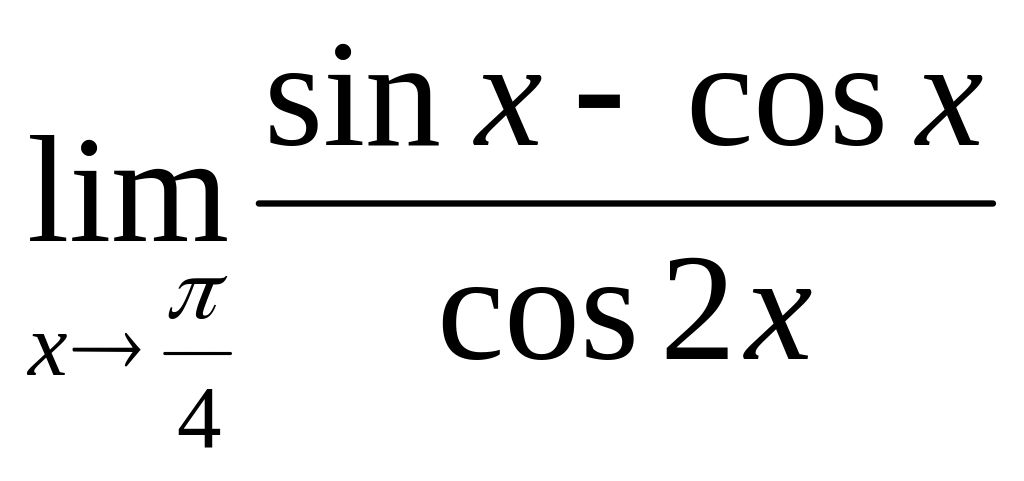 равен:
Ответ:
1) 2;
2) -2;
3) 0;
4)
равен:
Ответ:
1) 2;
2) -2;
3) 0;
4)
 (верный
ответ).
(верный
ответ).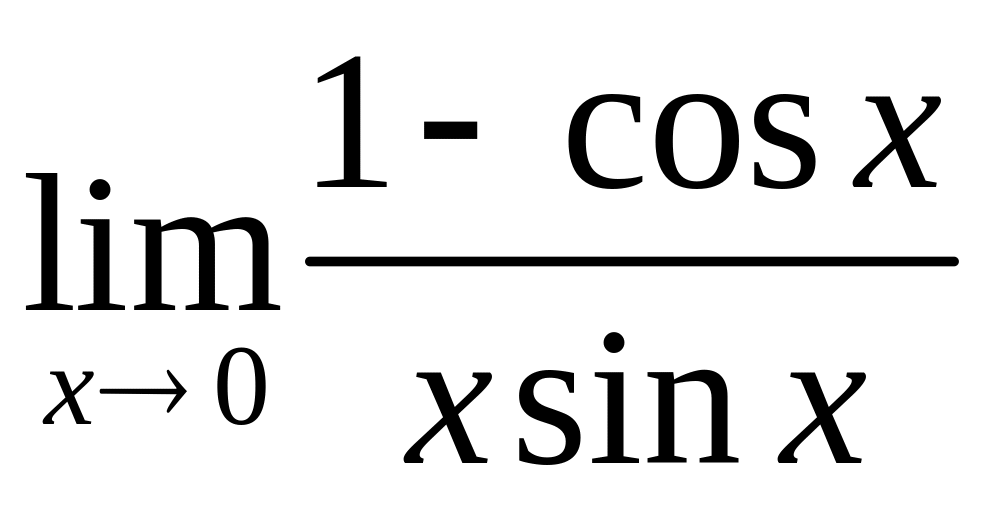 равен:
Ответ:
1)
равен:
Ответ:
1)
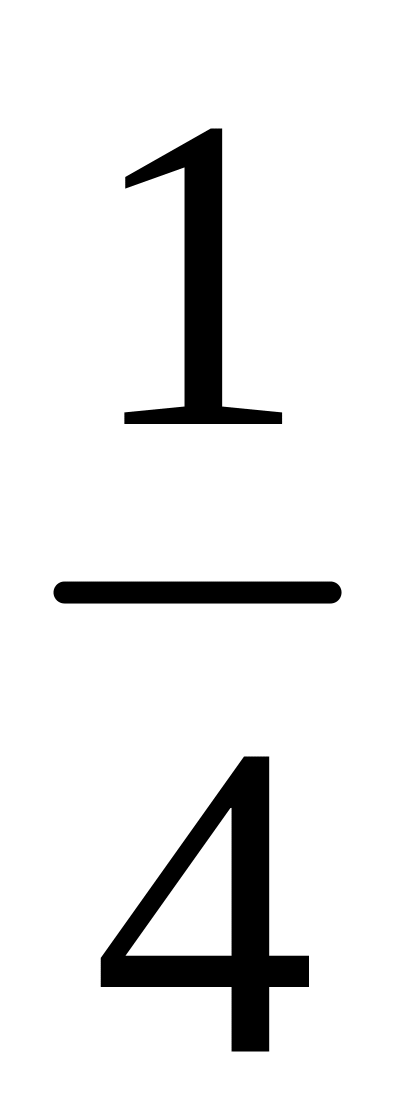 ;
2)
;
2)
 (верный
ответ);
3)
(верный
ответ);
3)
 ;
4)
;
4)
 .
.Предел функции
 равен
1)
равен
1)
 (верный ответ);
2)
;
3)
;
4)
(верный ответ);
2)
;
3)
;
4)
 .
.Предел функции
 равен
1)
равен
1)
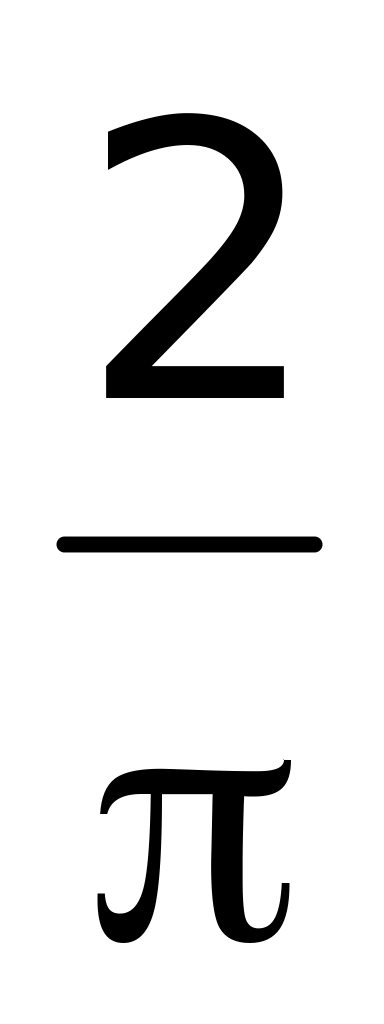 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
 ;
4)
;
4)
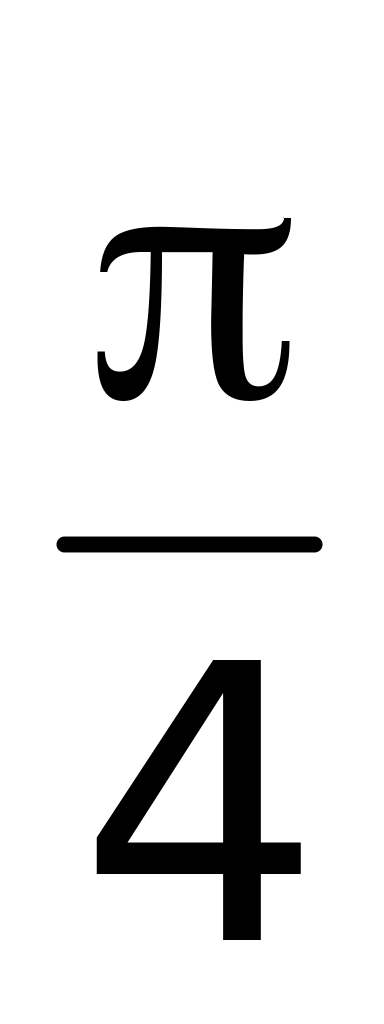 .
.Предел функции
 равен
1)
(верный ответ);
2)
;
3)
;
4)
.
равен
1)
(верный ответ);
2)
;
3)
;
4)
.Предел функции
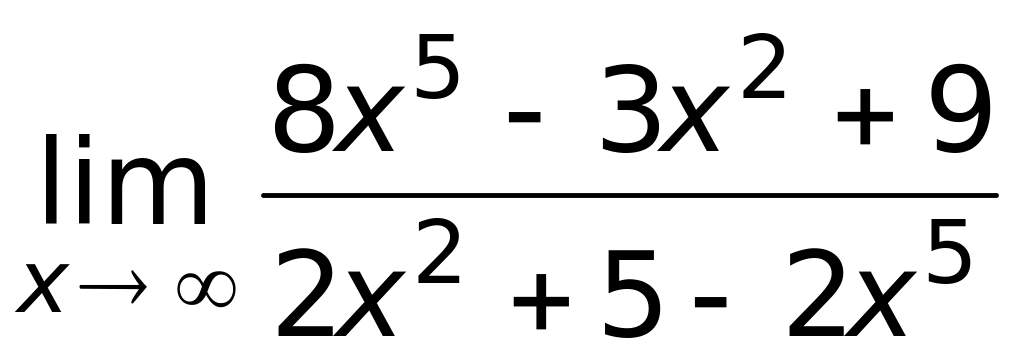 равен
1) –4 (верный ответ);
2) –3;
3)
;
4)
равен
1) –4 (верный ответ);
2) –3;
3)
;
4)
 .
. равен:
Ответ:
1) -1;
2) 1(верный ответ);
3) не
существует;
4) -2.
равен:
Ответ:
1) -1;
2) 1(верный ответ);
3) не
существует;
4) -2. равен:
Ответ:
1)
равен:
Ответ:
1)
 ;
2)
;
2)
 ;
3) не существует;
4)
;
3) не существует;
4)
 (верный
ответ).
(верный
ответ). равен:
Ответ:
1)
равен:
Ответ:
1)
 ;
2)
;
2)
 (верный
ответ);
3)
(верный
ответ);
3)
 ;
4) 5.
;
4) 5.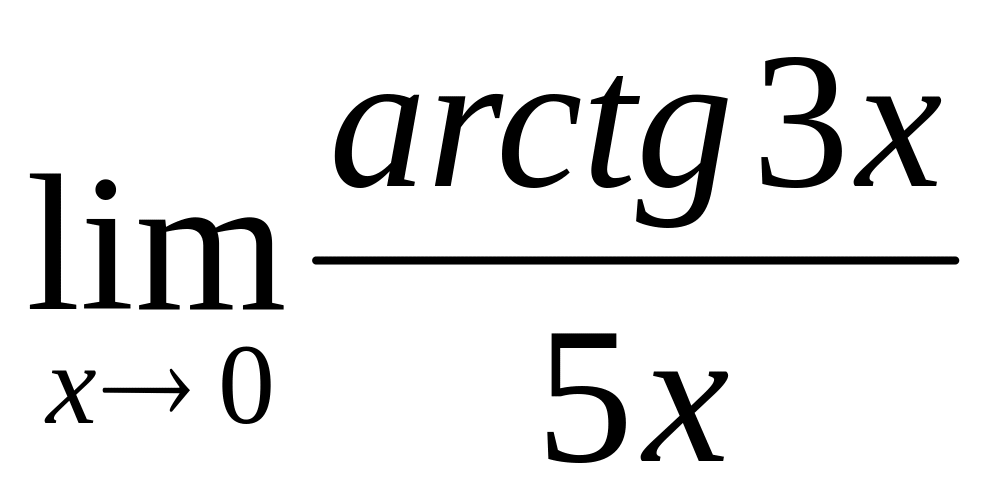 равен:
Ответ:
1)
равен:
Ответ:
1)
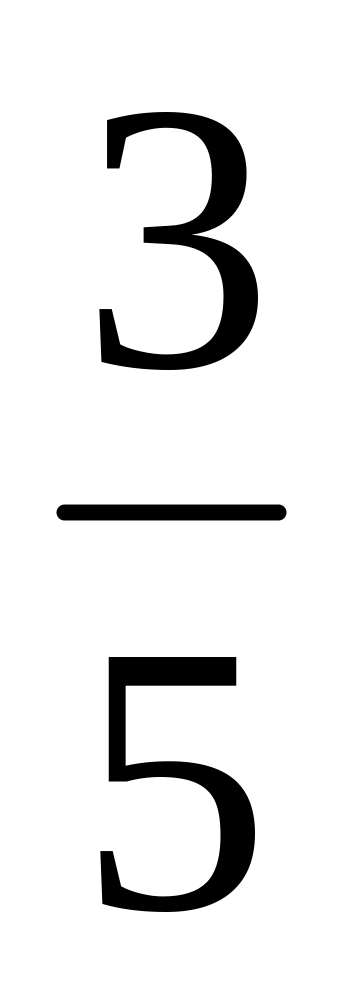 (верный
ответ);
2)
(верный
ответ);
2)
 ;
3) 3;
4) 5.
;
3) 3;
4) 5. равен:
Ответ:
1) 1;
2)
равен:
Ответ:
1) 1;
2)
 (верный ответ);
3)
;
4) 0.
(верный ответ);
3)
;
4) 0.Функция
 является монотонной на промежутках:
Ответ:
1)
является монотонной на промежутках:
Ответ:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 (верный ответ).
(верный ответ).Если функция
 убывает при всех значениях x,
то значение параметра а
принадлежит промежутку:
Ответ: 1)
убывает при всех значениях x,
то значение параметра а
принадлежит промежутку:
Ответ: 1)
 ;
2)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
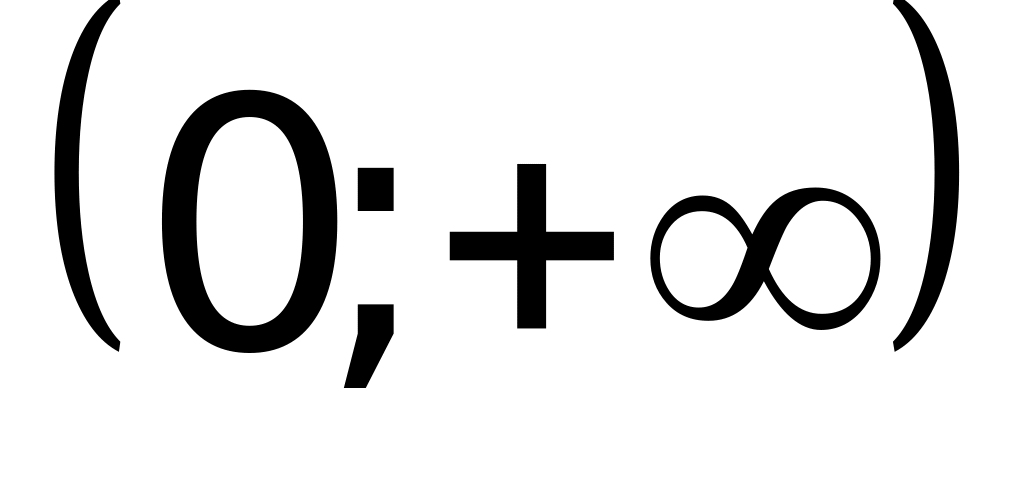 ;
4)
;
4)
 .
.Промежутками возрастания функции
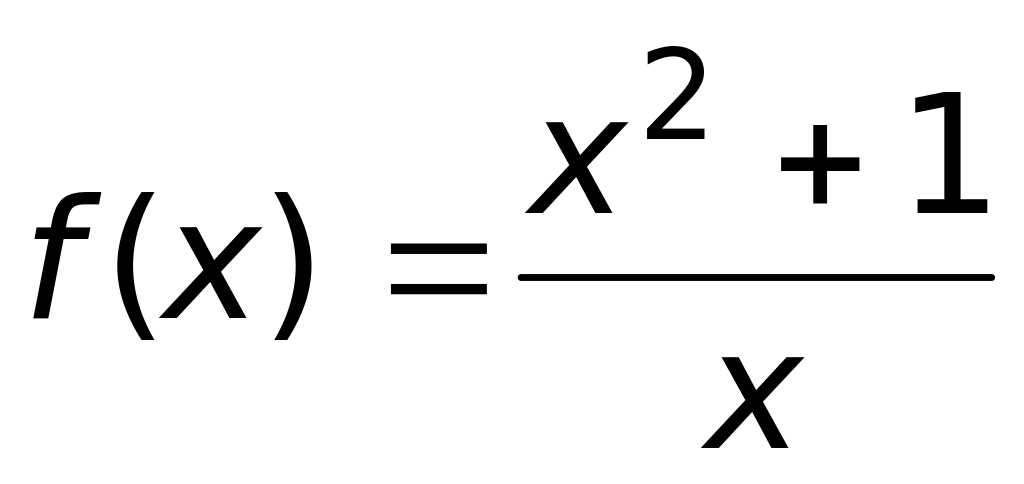 является:
Ответ: 1)
является:
Ответ: 1)
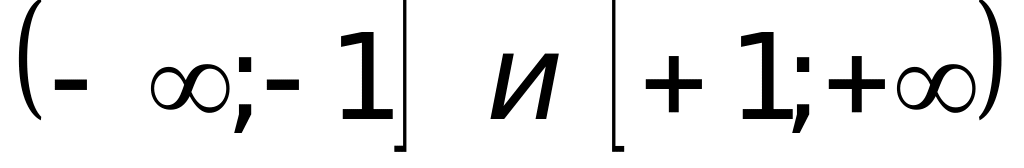 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
4)
;
3)
;
4)
 .
.Значения параметра а, при которых функция
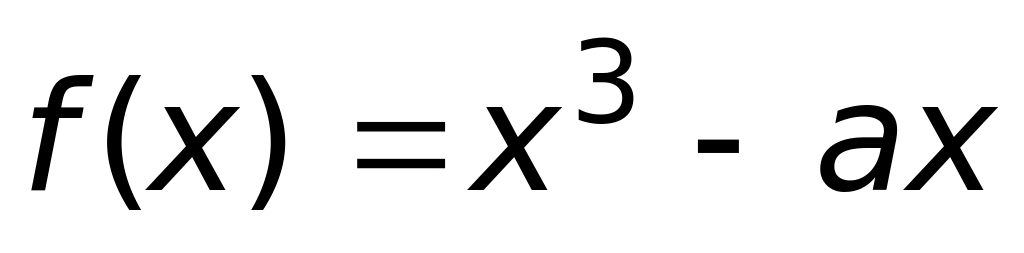 возрастает на всей числовой оси,
принадлежит промежутку:
Ответ: 1)
возрастает на всей числовой оси,
принадлежит промежутку:
Ответ: 1)
 ;
2)
;
2)
 (верный ответ);
3)
;
4)
.
(верный ответ);
3)
;
4)
.Число действительных корней производной многочлена
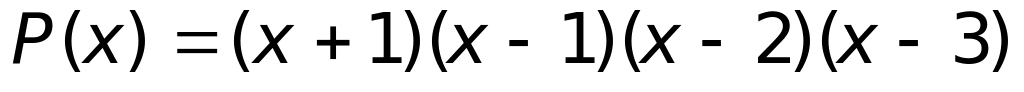 равно:
Ответ: 1) 3 (верный ответ);
2)
4;
3) 2;
4) невозможно определить.
равно:
Ответ: 1) 3 (верный ответ);
2)
4;
3) 2;
4) невозможно определить.Значения параметра а, при которых функция
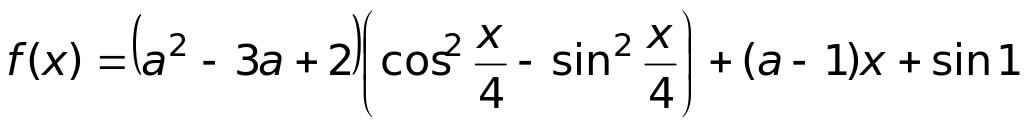 не имеет критических точек, принадлежат
промежутку:
Ответ: 1)
не имеет критических точек, принадлежат
промежутку:
Ответ: 1)
 ;
2)
;
2)
 ;
3)
или
;
3)
или
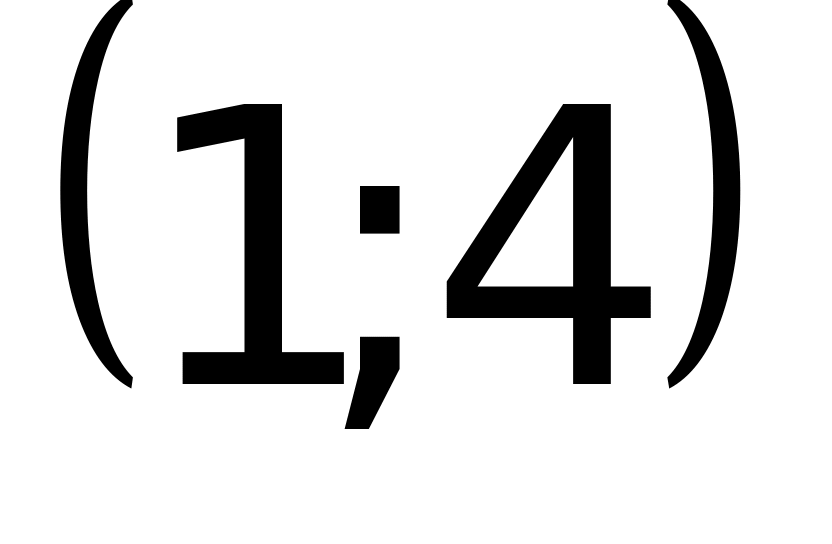 (верный ответ);
4) другой ответ.
(верный ответ);
4) другой ответ.Значения параметра а, при которых функция
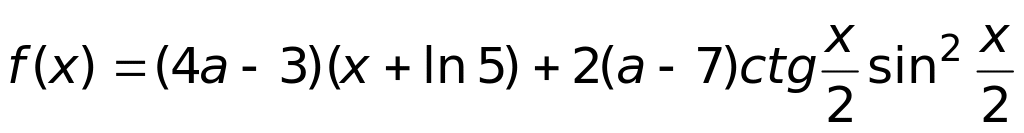 не имеет критических точек, принадлежат
промежутку:
Ответ: 1)
не имеет критических точек, принадлежат
промежутку:
Ответ: 1)
 ;
2)
или
;
2)
или
 (верный ответ);
3)
(верный ответ);
3)
 ;
4) другой ответ.
;
4) другой ответ.Значения параметра а, при которых среди корней уравнения
 имеются два равных, следующие:
Ответ:
1)
имеются два равных, следующие:
Ответ:
1)
 (верный ответ);
2)
(верный ответ);
2)
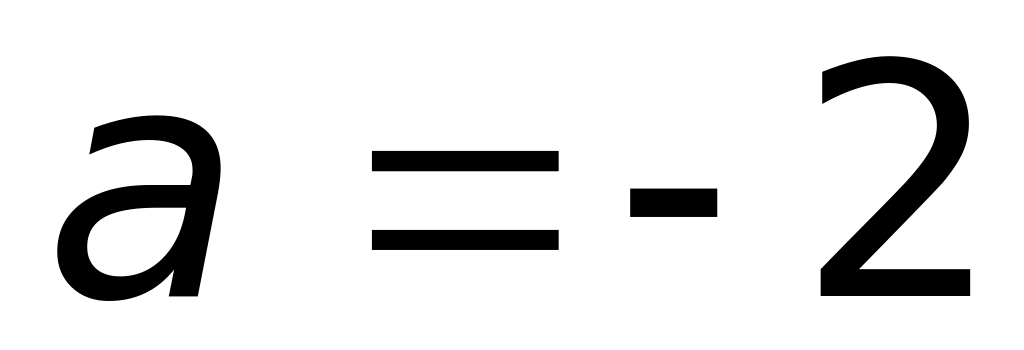 ;
3)
;
3)
 ;
4)
;
4)
 .
.Уравнение
 имеет:
Ответ: 1) только один действительный
корень (верный ответ);
2) три
действительных корня, среди которых
два равных;
3) три различных
действительных корня;
4) другой
ответ.
имеет:
Ответ: 1) только один действительный
корень (верный ответ);
2) три
действительных корня, среди которых
два равных;
3) три различных
действительных корня;
4) другой
ответ.Если трехчлен
 имеет минимум при
имеет минимум при
 ,
причем этот минимум равен 5, то значения
параметров
,
причем этот минимум равен 5, то значения
параметров
 и
и
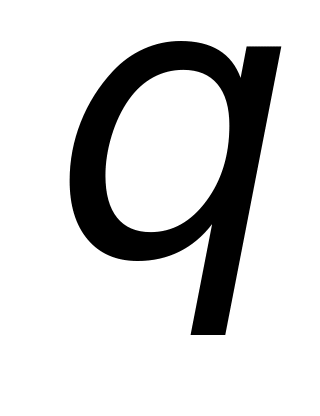 равны:
Ответ: 1)
равны:
Ответ: 1)
 ;
2)
;
2)
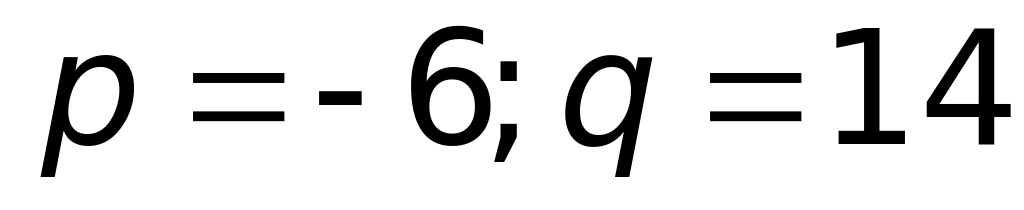 (верный ответ);
3)
(верный ответ);
3)
 ;
4)
;
4)
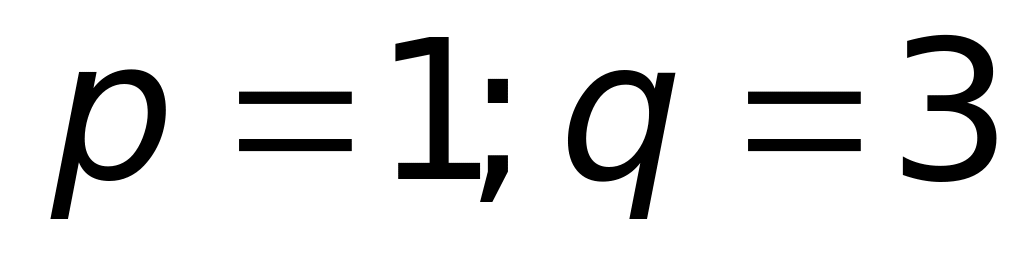 .
.Все корни многочлена
 действительные и разные. Тогда производная
этого многочлена имеет:
Ответ: 1) n
действительных корней;
2) по крайней
мере (n-1)
действительный корень;
3) точно (n-1)
действительный корень (верный ответ);
4)
невозможно определить.
действительные и разные. Тогда производная
этого многочлена имеет:
Ответ: 1) n
действительных корней;
2) по крайней
мере (n-1)
действительный корень;
3) точно (n-1)
действительный корень (верный ответ);
4)
невозможно определить.Наибольшее значение параметра а, при котором
 является точкой экстремума функции
является точкой экстремума функции
 ,
равно:
Ответ: 1) 10;
2) 5;
3) 7 (верный
ответ);
4) –3.
,
равно:
Ответ: 1) 10;
2) 5;
3) 7 (верный
ответ);
4) –3.Значение параметра с, при котором функция
 не имеет экстремума в критической
точке, равно:
Ответ: 1) 1,92 (верный
ответ);
2) –10,08;
3) 2;
4) –10.
не имеет экстремума в критической
точке, равно:
Ответ: 1) 1,92 (верный
ответ);
2) –10,08;
3) 2;
4) –10.Число точек экстремума функции
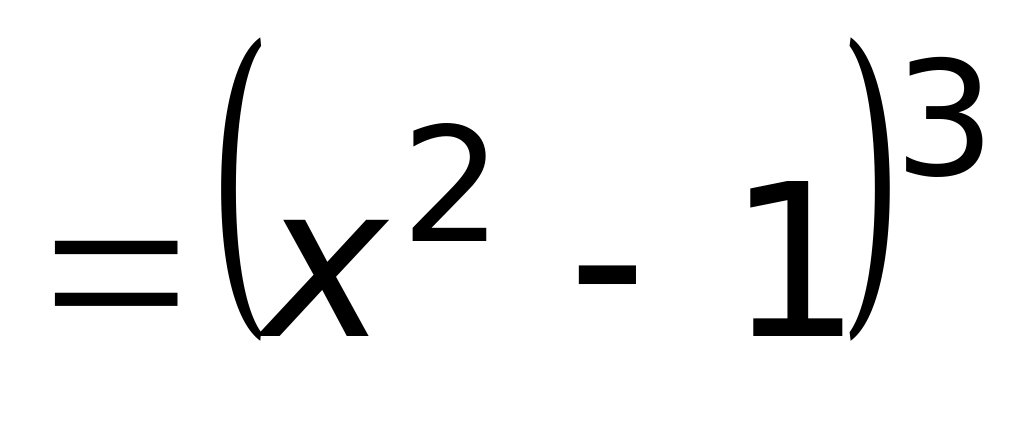 равно:
Ответ: 1) 2;
2) 3;
3) 6;
4)
1 (верный ответ).
равно:
Ответ: 1) 2;
2) 3;
3) 6;
4)
1 (верный ответ).Наименьшее значение функции
 на отрезке
на отрезке
 равно:
Ответ: 1)
равно:
Ответ: 1)
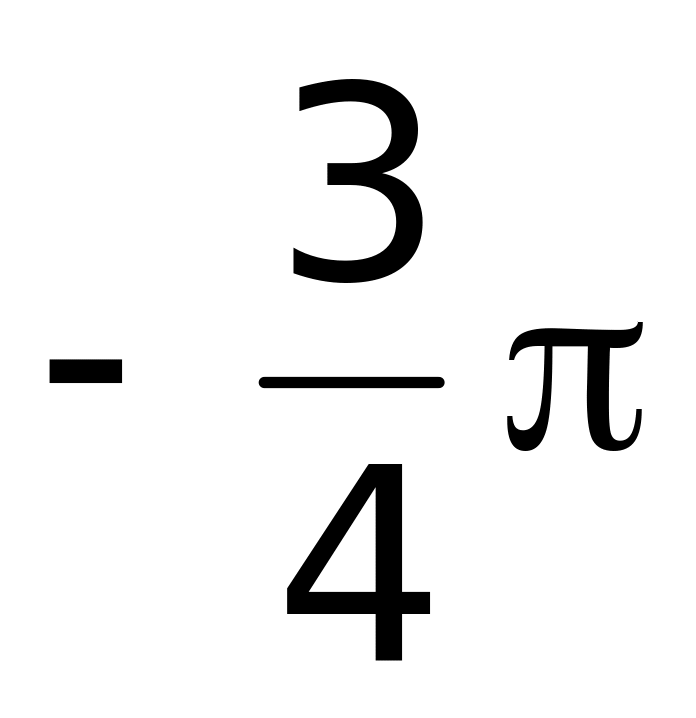 ;
2)
;
2)
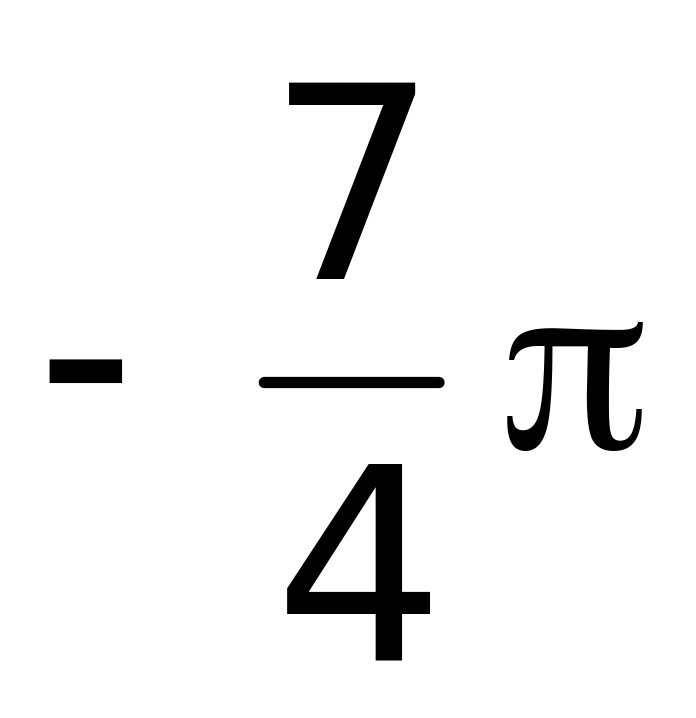 ;
3)
;
3)
 (верный ответ);
4) другой ответ.
(верный ответ);
4) другой ответ.Точка
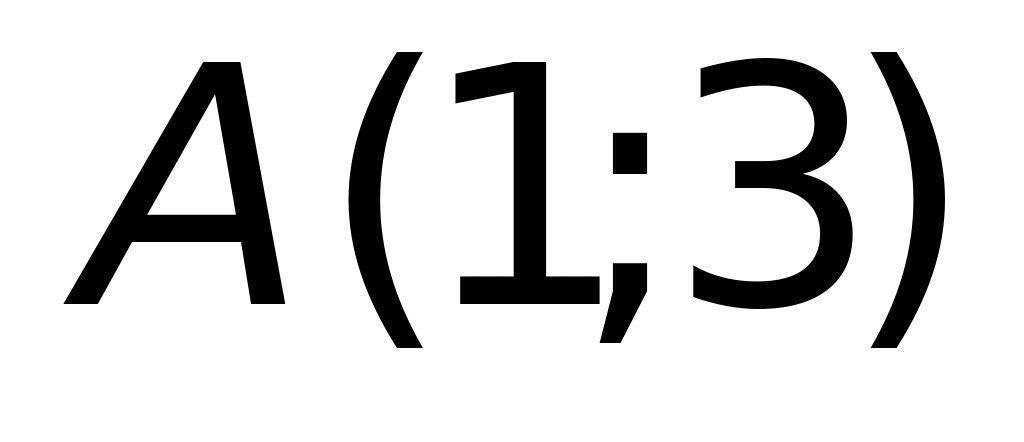 является точкой перегиба кривой
является точкой перегиба кривой
 при значениях параметров а
и b,
равных:
Ответ: 1)
при значениях параметров а
и b,
равных:
Ответ: 1)
 (верный ответ);
2)
(верный ответ);
2)
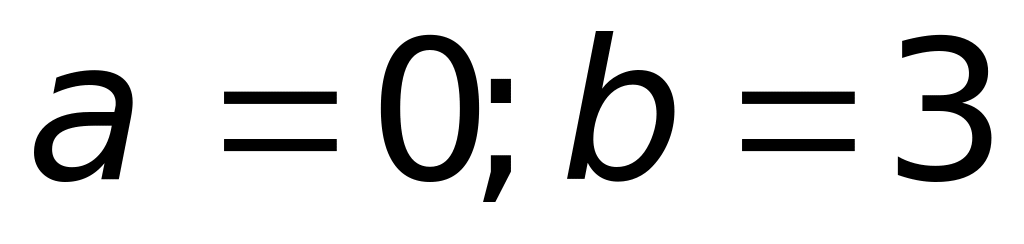 ;
3)
;
3)
 ;
4) другой ответ.
;
4) другой ответ.Уравнение касательной к графику функции
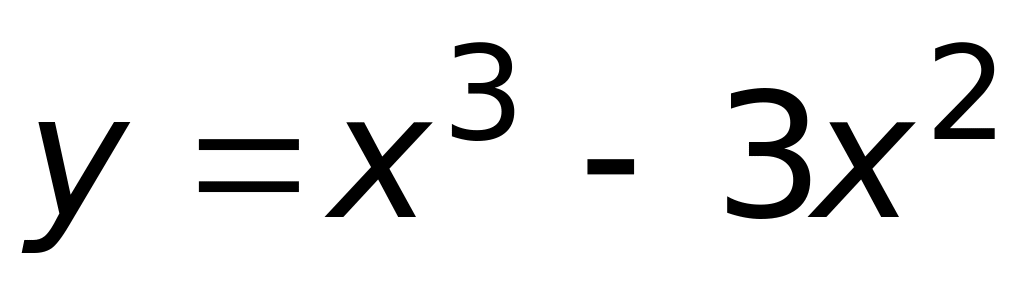 в точке минимума этой функции имеет
вид:
Ответ: 1)
в точке минимума этой функции имеет
вид:
Ответ: 1)
 ;
2)
;
2)
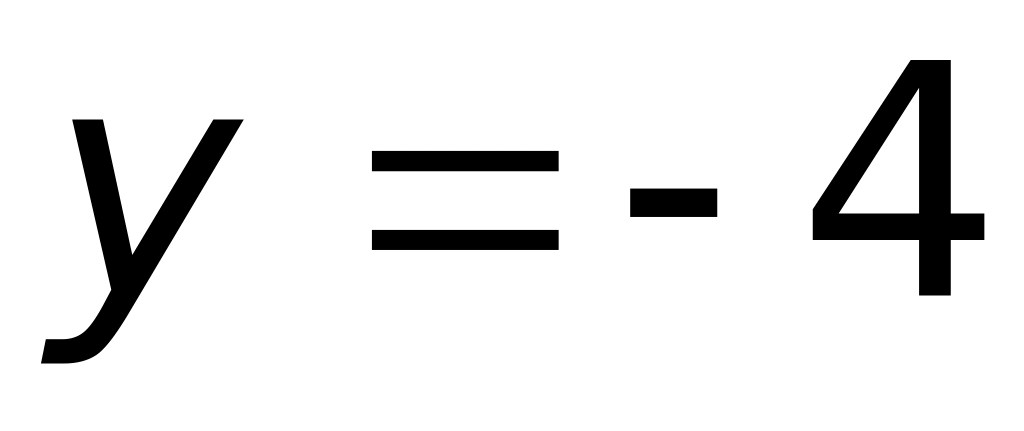 (верный ответ);
3)
(верный ответ);
3)
 ;
4)
;
4)
 .
.График функции
 является выпуклой кривой на интервале:
Ответ: 1)
;
2)
является выпуклой кривой на интервале:
Ответ: 1)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
 ;
4) другой ответ.
;
4) другой ответ.Число асимптот графика функции
 равно:
Ответ: 1) 2;
2) 1;
3) 3 (верный
ответ);
4) 0.
равно:
Ответ: 1) 2;
2) 1;
3) 3 (верный
ответ);
4) 0.Функция
 принимает наименьшее значение на
отрезке
принимает наименьшее значение на
отрезке
 в точке:
Ответ: 1)
в точке:
Ответ: 1)
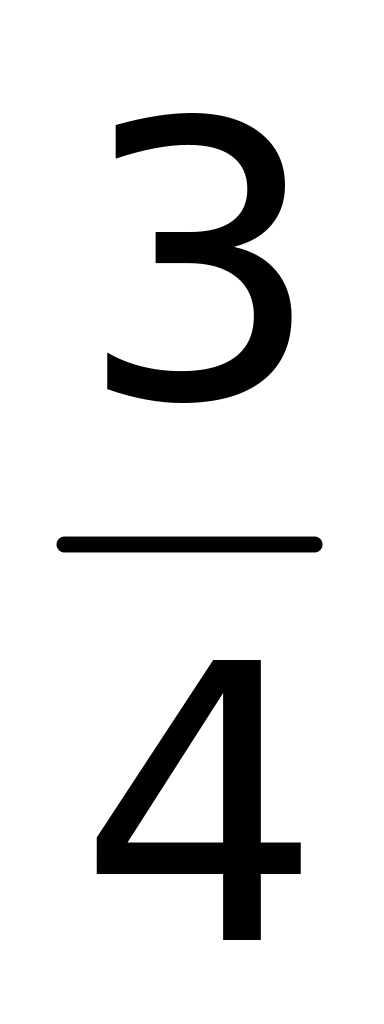 ;
2) 1 (верный ответ);
3) 2;
4)
.
;
2) 1 (верный ответ);
3) 2;
4)
.Представление числа 12 в виде суммы двух положительных слагаемых, таких что сумма их квадратов принимает наименьшее значение, имеет вид: Ответ: 1) 4+8; 2) 6+6 (верный ответ); 3) 5+7; 4) 3+9.
График четной функции имеет асимптоту
 при
при
 .
Тогда уравнение асимптоты при
.
Тогда уравнение асимптоты при
 имеет вид:
Ответ:
имеет вид:
Ответ:
 (верный ответ);
2)
(верный ответ);
2)
 ;
3)
;
3)
 ;
4) невозможно определить.
;
4) невозможно определить.Кривая
 имеет следующие асимптоты:
Ответ:
1)
имеет следующие асимптоты:
Ответ:
1)
 ;
2)
;
2)
 (верный ответ);
3)
(верный ответ);
3)
 ;
4) только
;
4) только
 .
.Функция
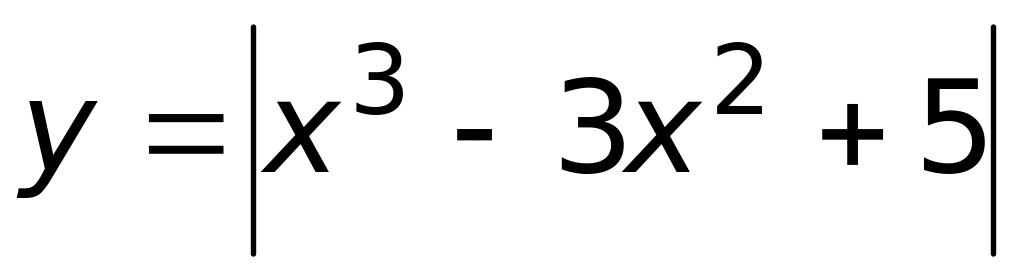 принимает наименьшее значение на
отрезке
принимает наименьшее значение на
отрезке
 в точке:
Ответ: 1) 0;
2) 1;
3) 2 (верный
ответ);
4) 3.
в точке:
Ответ: 1) 0;
2) 1;
3) 2 (верный
ответ);
4) 3.Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке

Ответ: а)![]() ,
,
![]() (верный
ответ);
б)
(верный
ответ);
б)
![]() ,
,
![]() ;
в)
;
в)
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() .
.
Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке

Ответ: а)![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ;
в)
;
в)
![]() ,
,
![]() (верный
ответ);
г)
(верный
ответ);
г)
![]() ,
,
![]() .
.
Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке

Ответ: а)![]() ,
,
![]() ;
б)
,
;
б)
,
![]() (верный
ответ);
в)
(верный
ответ);
в)
![]() ,
,
![]() ;
г)
;
г)
![]() ,
,
![]() .
.
Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке

Ответ: а)![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ;
в)
;
в)
![]() ,
;
г)
,
(верный
ответ).
,
;
г)
,
(верный
ответ).
Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке

Ответ: а)![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
![]() ;
в)
;
в)
![]() ,
(верный
ответ);
г)
,
(верный
ответ);
г)
![]() ,
.
,
.
