
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО КУРСУ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
Для студентов
физико-математического факультета
Могилев 2012
Введение в анализ
Найти область определения функции
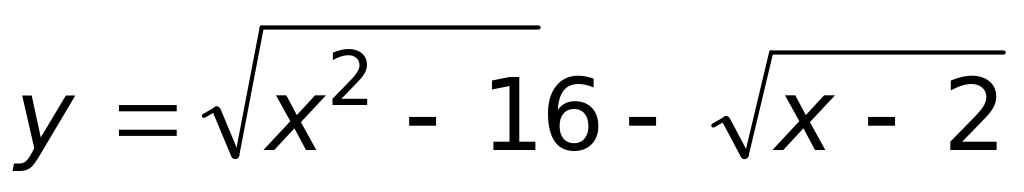 Ответ:
а)
Ответ:
а)
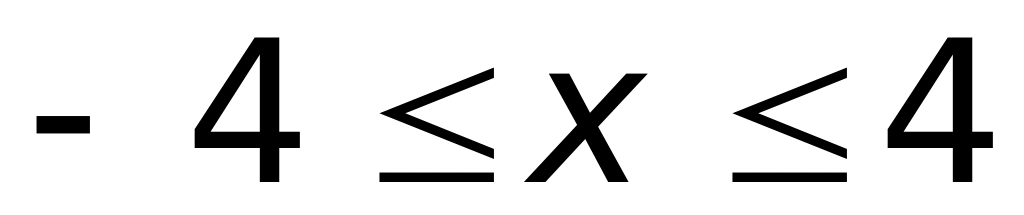 ;
б)
;
б)
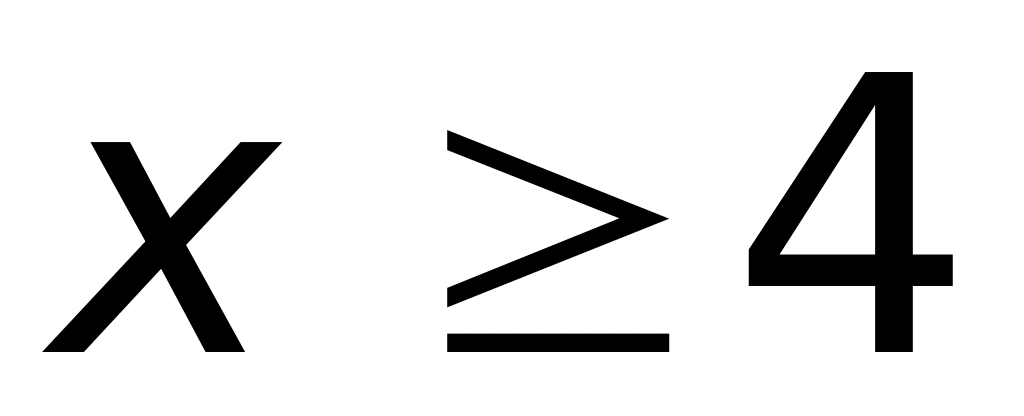 (верный ответ);
в)
(верный ответ);
в)
 ;
г)
;
г)
 .
.Найти область определения функции
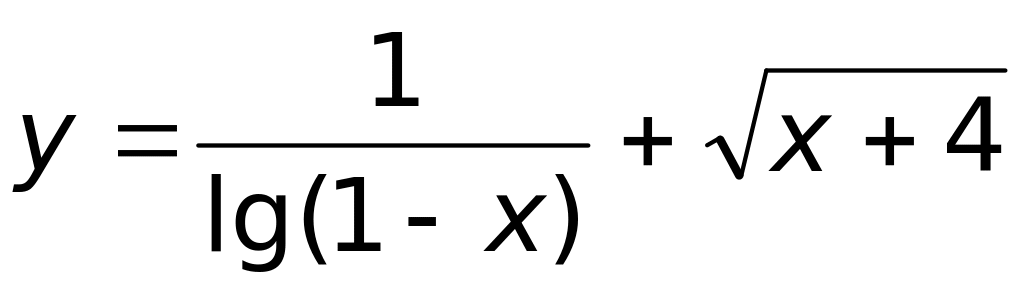 Ответ:
а)
Ответ:
а)
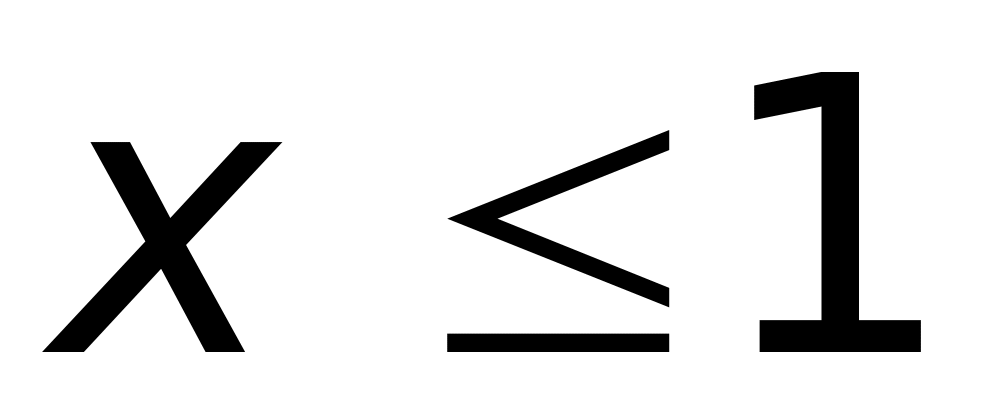 ;
б)
;
б)
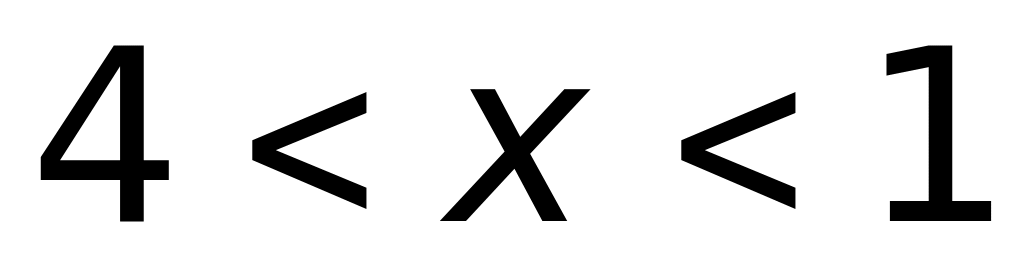 ;
в)
;
в)
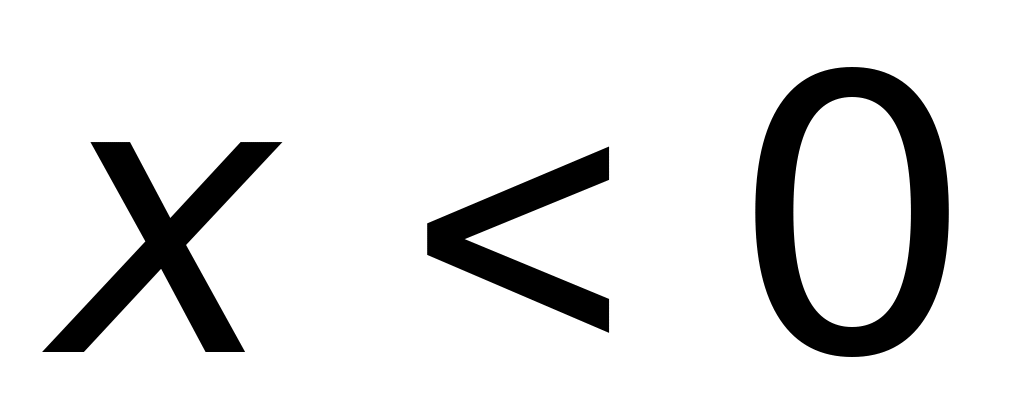 ;
г)
;
г)
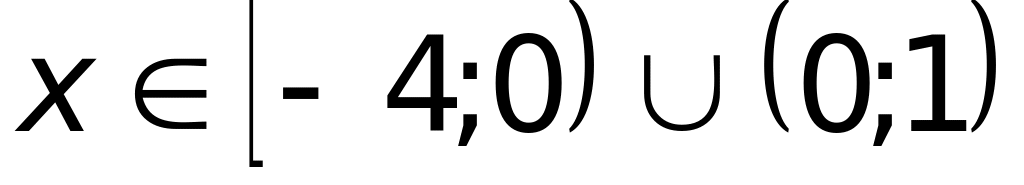 (верный
ответ).
(верный
ответ).Найти область определения функции
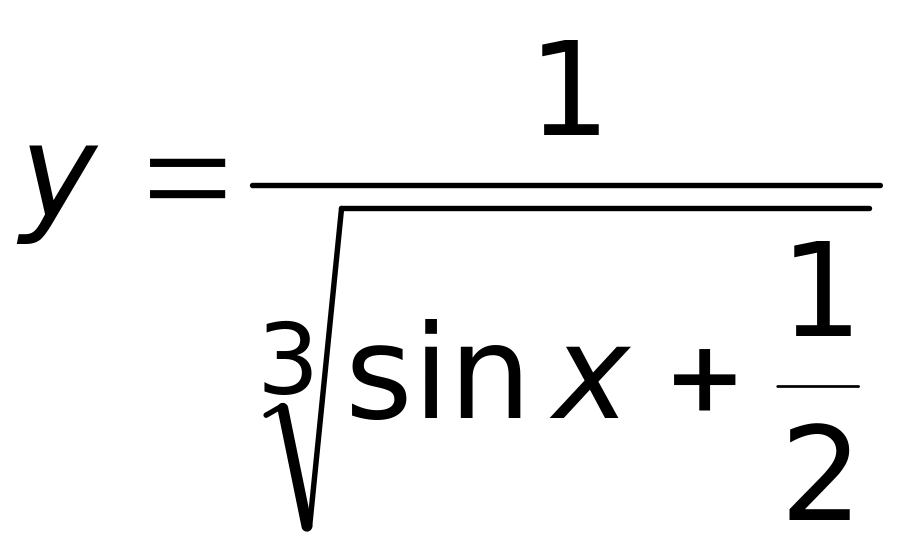 Ответ:
а)
Ответ:
а)
 (верный
ответ);
б)
(верный
ответ);
б)
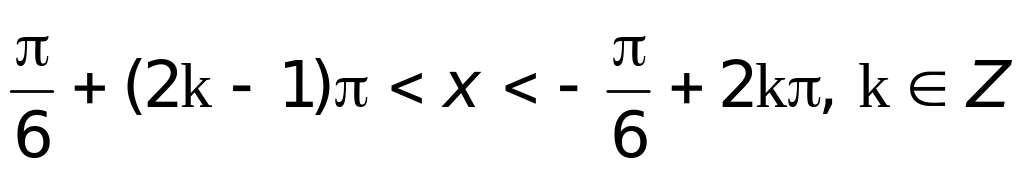 ;
в)
;
в)
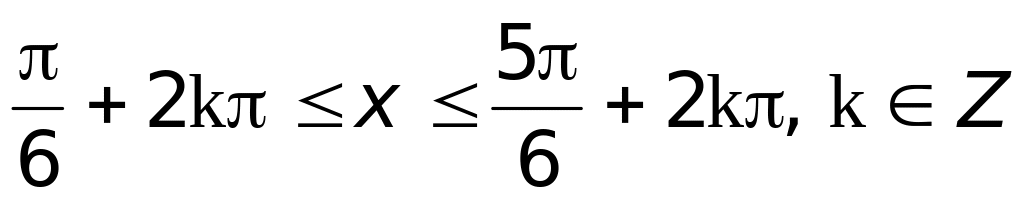 ;
г)
;
г)
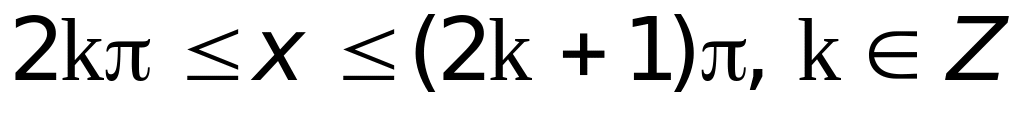 .
.
Какие из указанных функций являются четными, какие нечетными, какие не являются ни четными, ни нечетными 1)
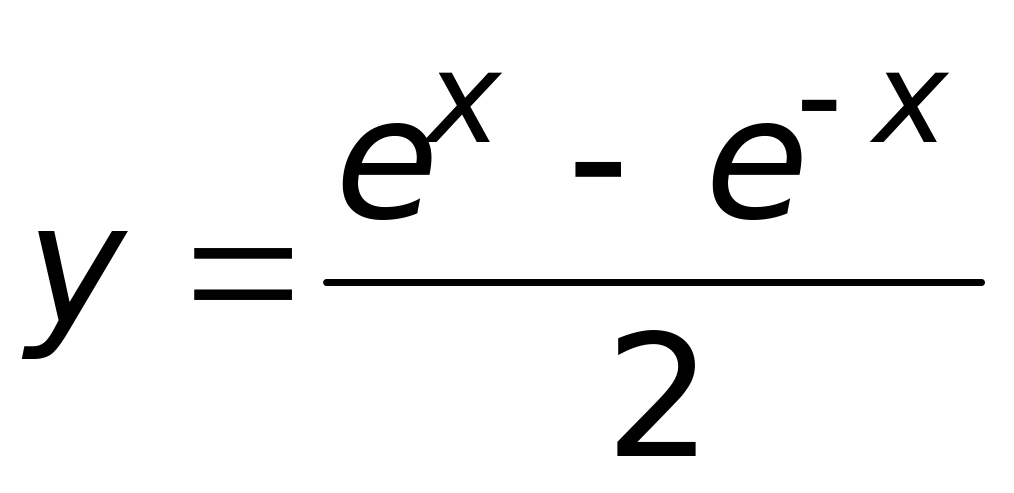 ;
2)
;
2)
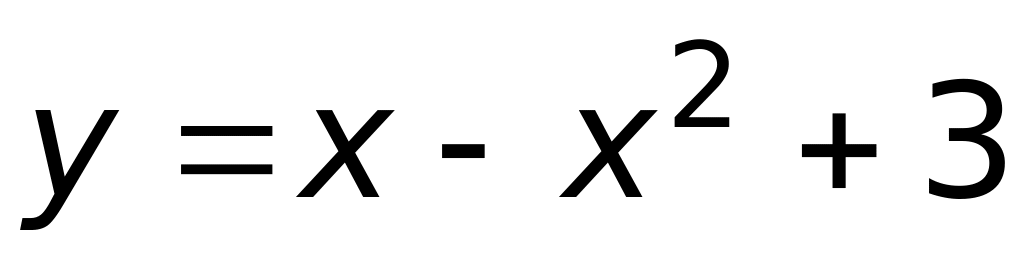 ;
3)
;
3)
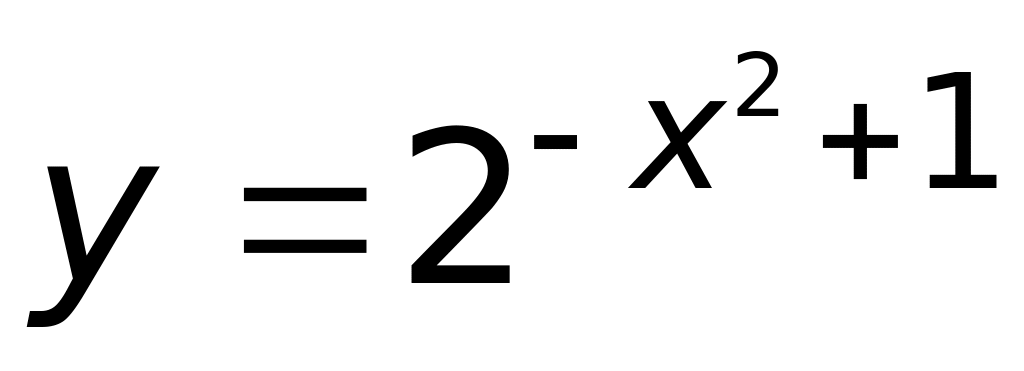 ?
Ответ:
а) 1, 3 – четные, 2 – нечетная и не нечетная;
б) 1, 2 – не четные и не нечетные, 3 –
четная;
в) все функции не являются
ни четными и ни нечетными;
г) 1 –
нечетная, 2 – не является ни четной, ни
нечетной, 3 – четная (верный ответ).
?
Ответ:
а) 1, 3 – четные, 2 – нечетная и не нечетная;
б) 1, 2 – не четные и не нечетные, 3 –
четная;
в) все функции не являются
ни четными и ни нечетными;
г) 1 –
нечетная, 2 – не является ни четной, ни
нечетной, 3 – четная (верный ответ).Какие из перечисленных функций являются периодическими и какой у них наименьший положительный период 1)
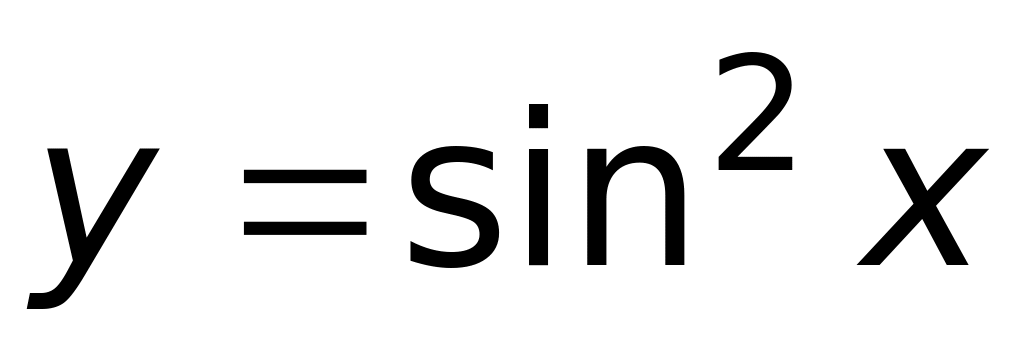 ;
2)
;
2)
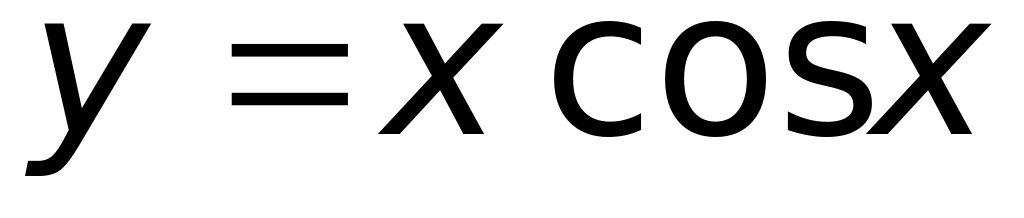 ;
3)
;
3)
 ?
Ответ:
а) 1 и 3 – периодические,
?
Ответ:
а) 1 и 3 – периодические,
 ;
б) 1 – периодическая,
;
б) 1 – периодическая,
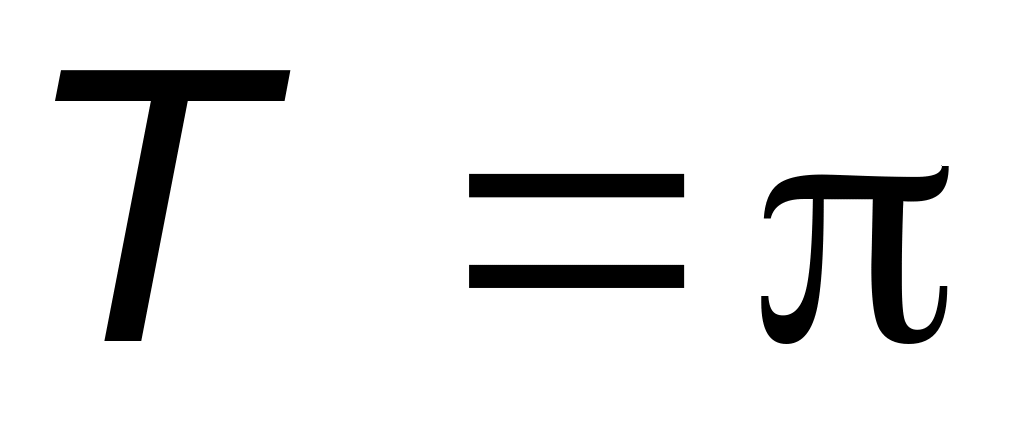 ,
2 – периодическая,
;
в) 1 – периодическая,
(верный ответ);
г) 1 – периодическая,
.
,
2 – периодическая,
;
в) 1 – периодическая,
(верный ответ);
г) 1 – периодическая,
.Зная график функции
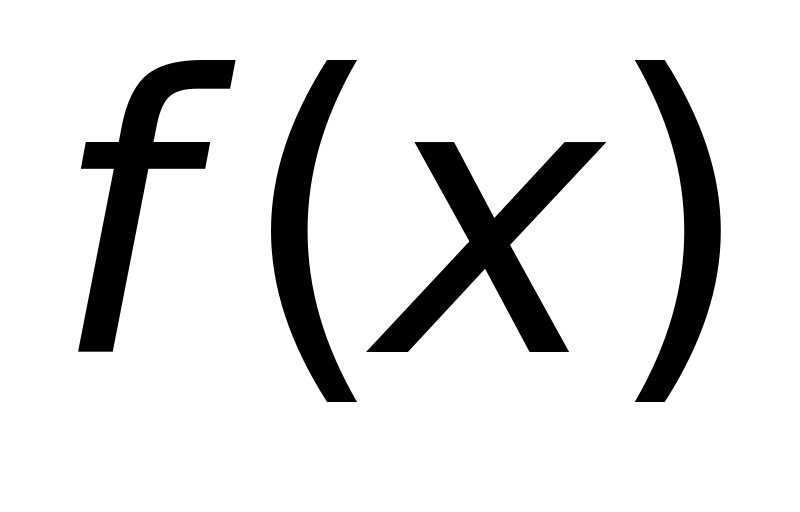 ,
построить график функции
,
построить график функции
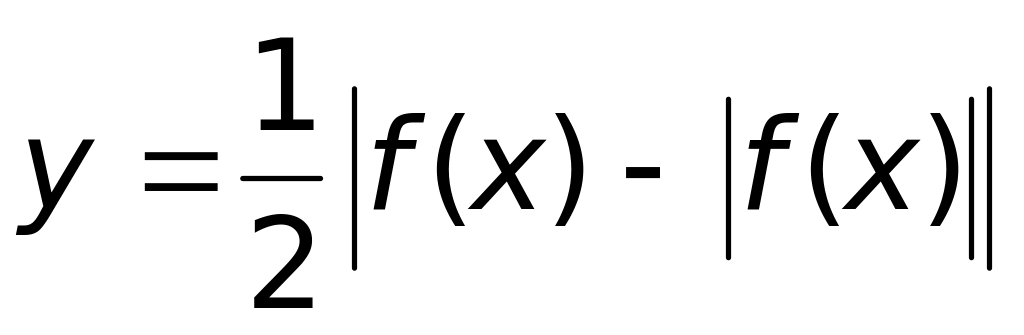 Ответ:
а)
Ответ:
а)
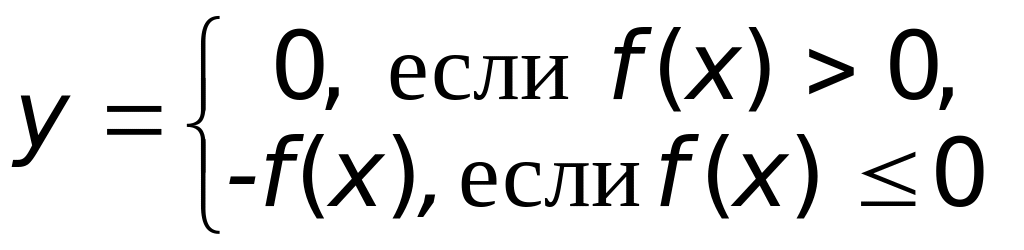 (верный ответ);
б)
(верный ответ);
б)
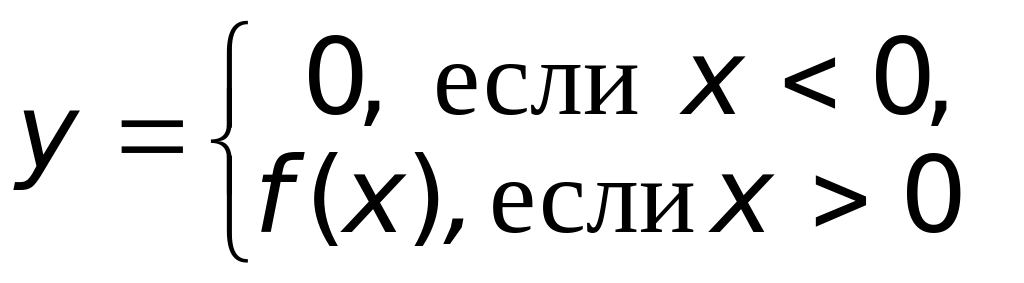 ;
в)
;
в)
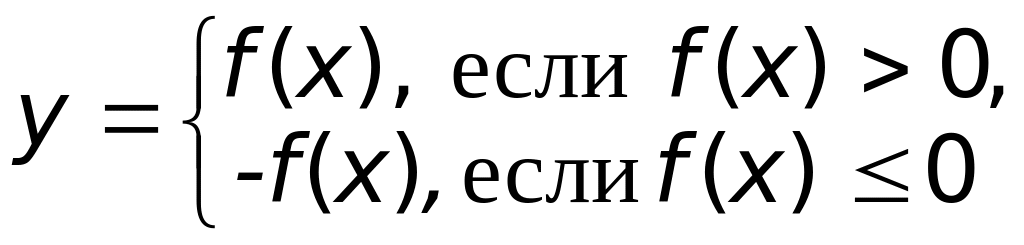 ;
г)
;
г)

Найти
 Ответ: а)
Ответ: а)
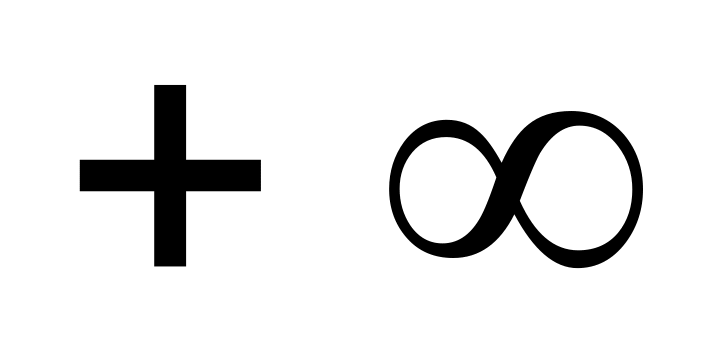 ;
б)
;
б)
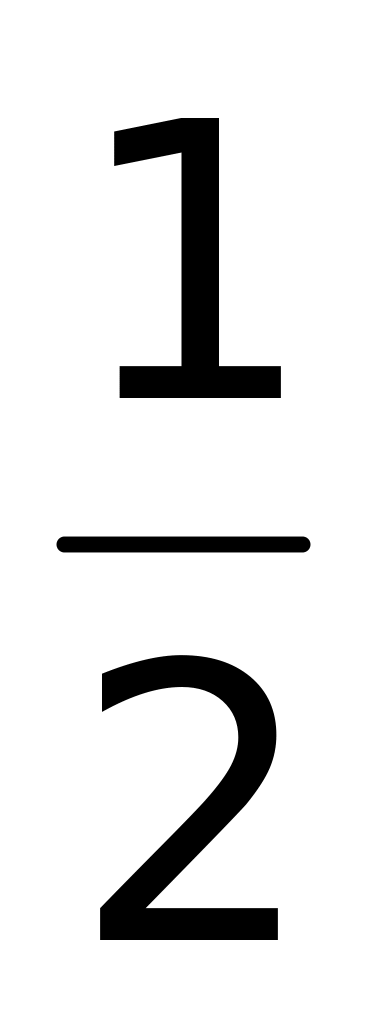 ;
в) 2(верный ответ);
г) 1.
;
в) 2(верный ответ);
г) 1.Найти
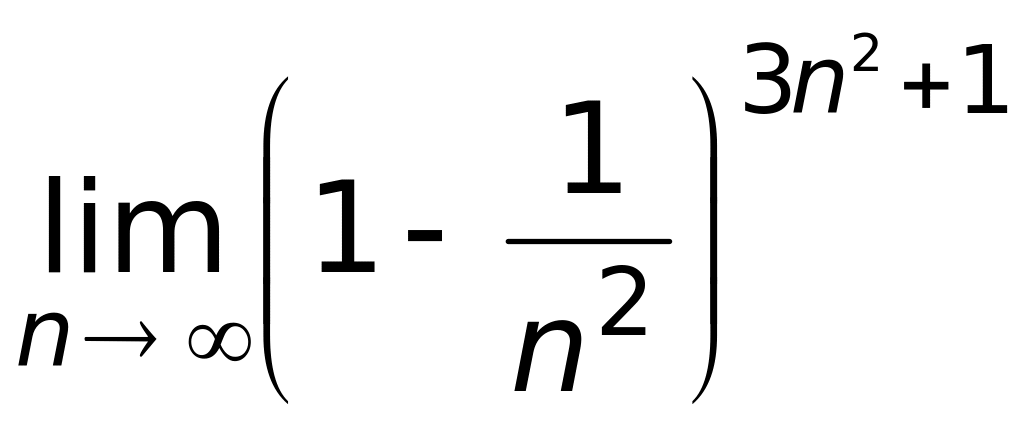 Ответ: а)
Ответ: а)
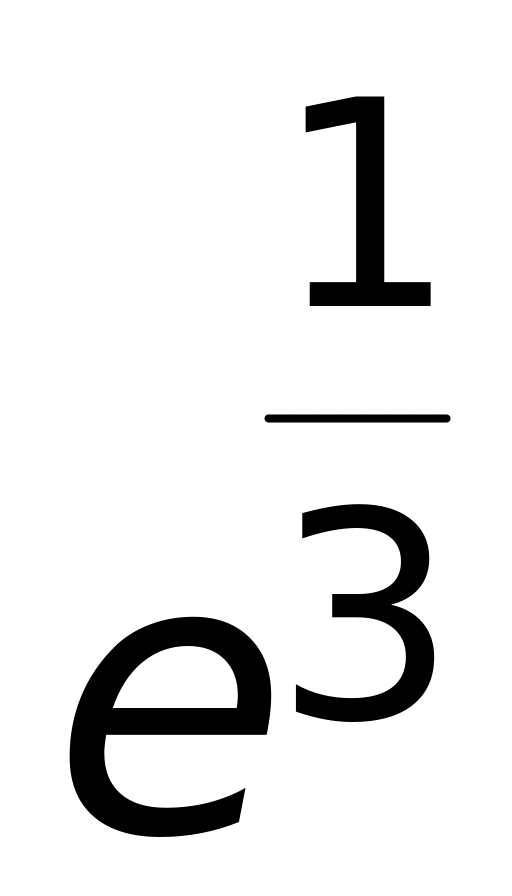 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
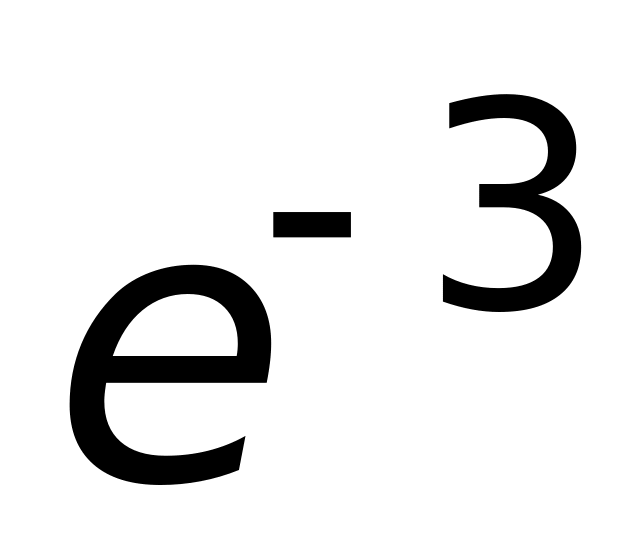 (верный
ответ).
(верный
ответ).Найти
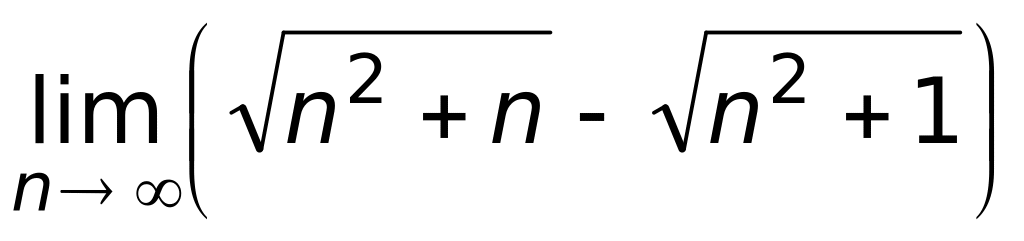 Ответ: а) 0;
б)
;
в) 1;
г)
(верный
ответ).
Ответ: а) 0;
б)
;
в) 1;
г)
(верный
ответ).Найти
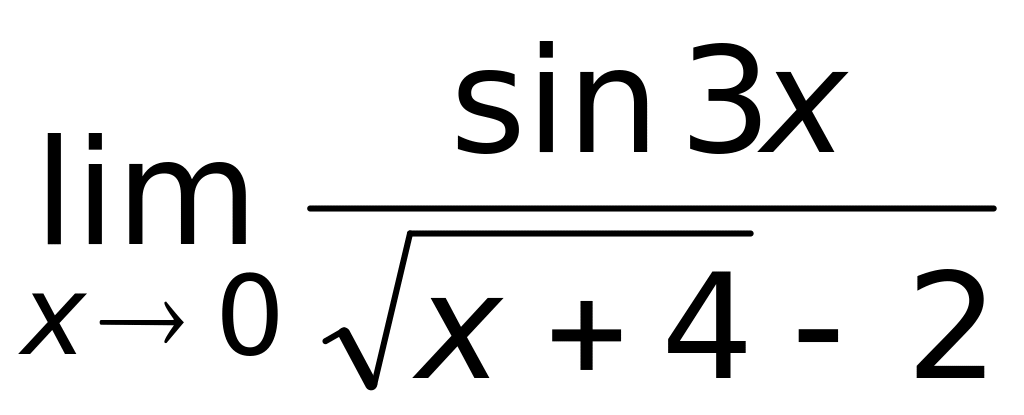 Ответ: а) 12(верный ответ);
б) 4;
в)
3;
г)
Ответ: а) 12(верный ответ);
б) 4;
в)
3;
г)
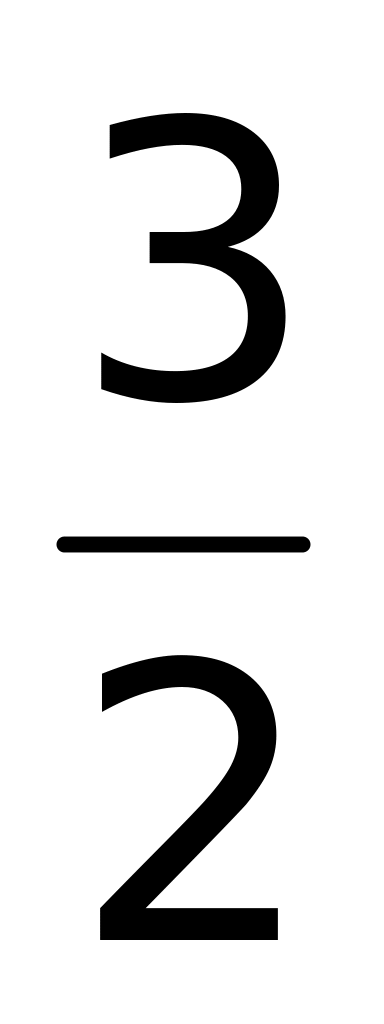 .
.Найти
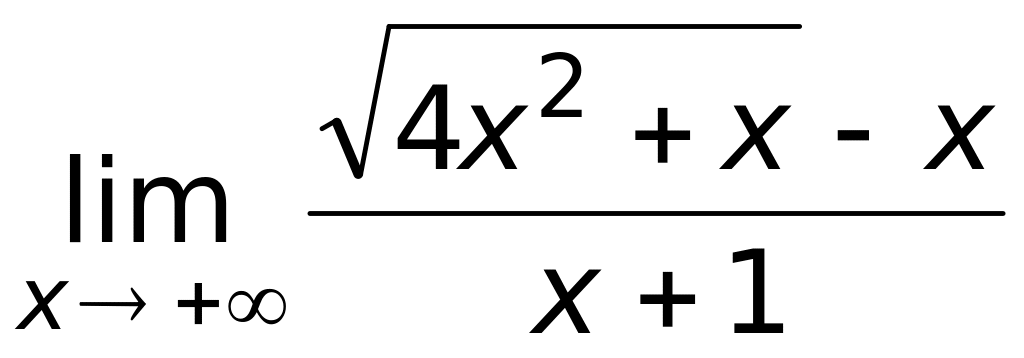
Ответ: а) ; б) 3; в) 2; г) 1(верный ответ).
Найти
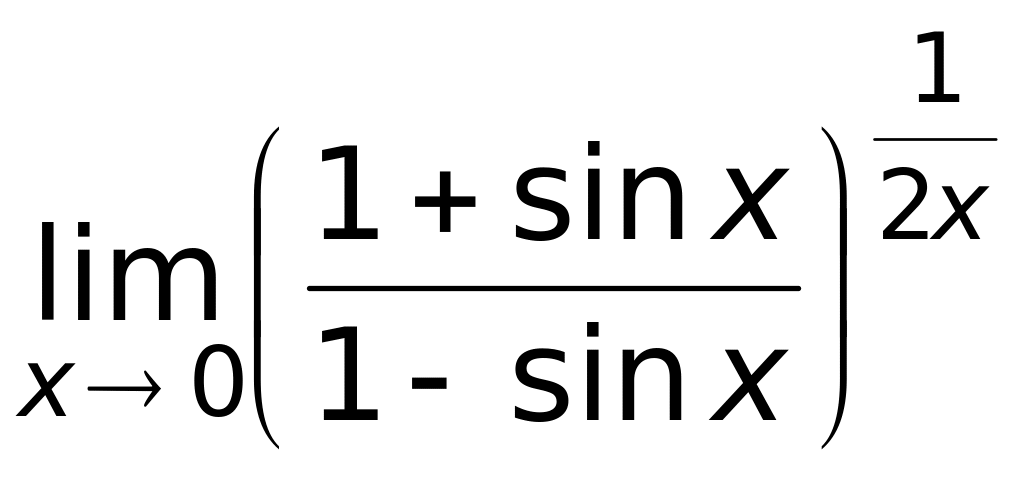 Ответ: а)
;
б) 2;
в)
Ответ: а)
;
б) 2;
в)
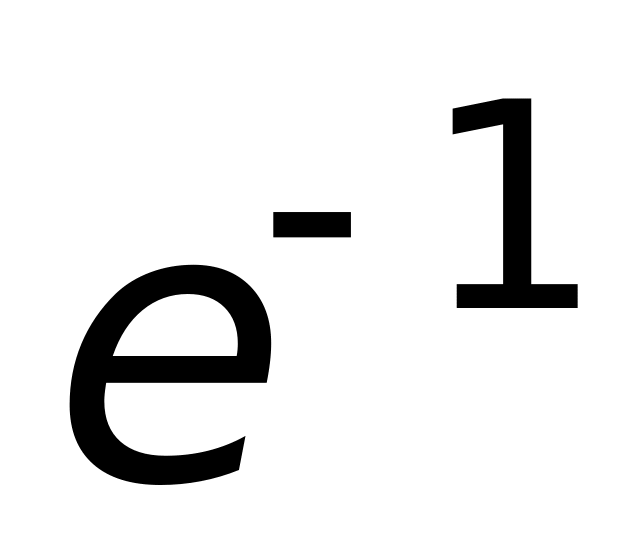 ;
г)
;
г)
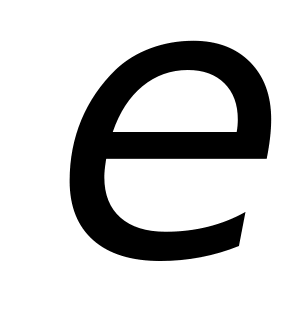 (верный
ответ).
(верный
ответ).Найти
 Ответ: а)
Ответ: а)
 ;
б)
;
б)
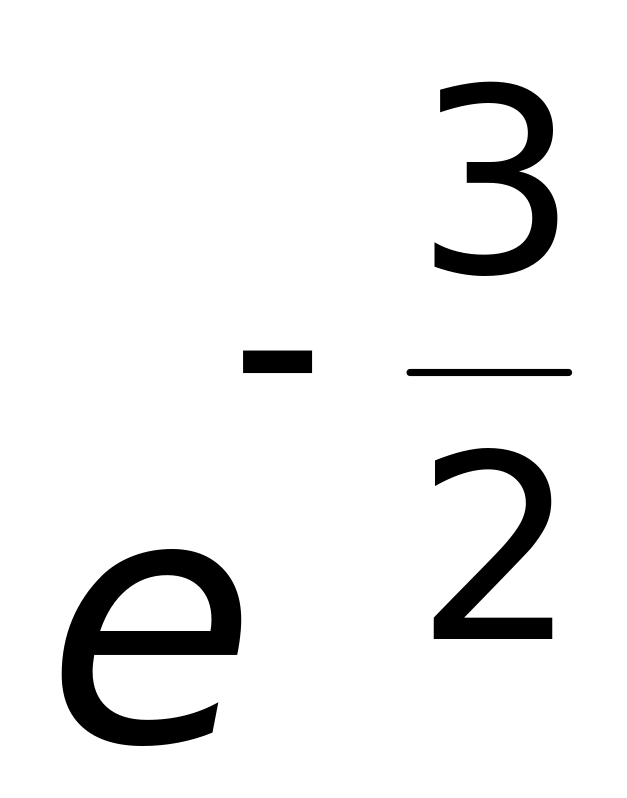 (верный
ответ);
в)
;
г)
(верный
ответ);
в)
;
г)
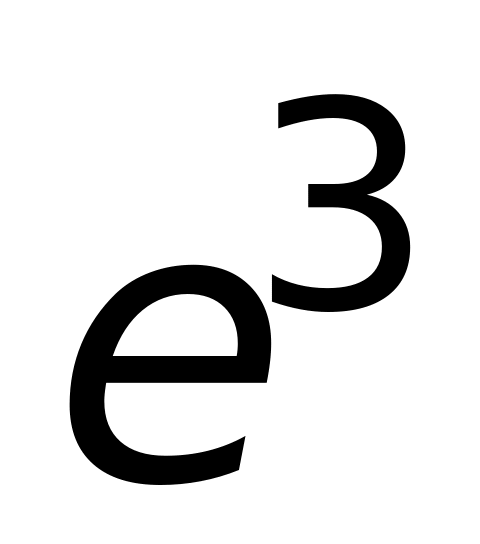 .
.Найти
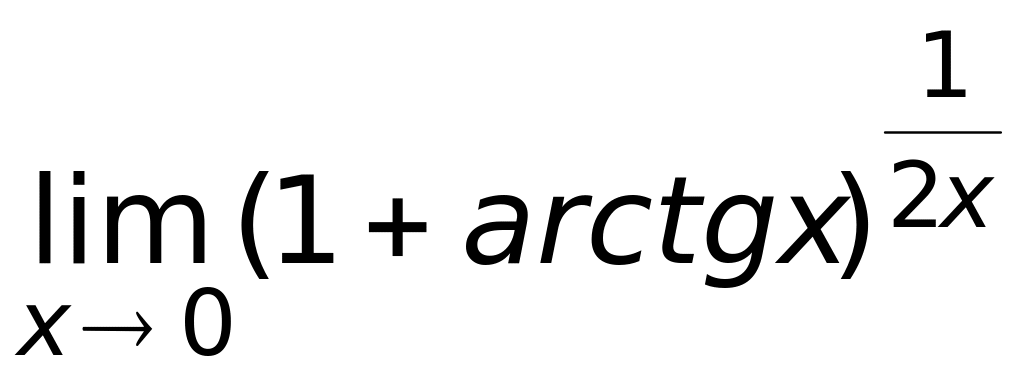 Ответ: а)
;
б)
Ответ: а)
;
б)
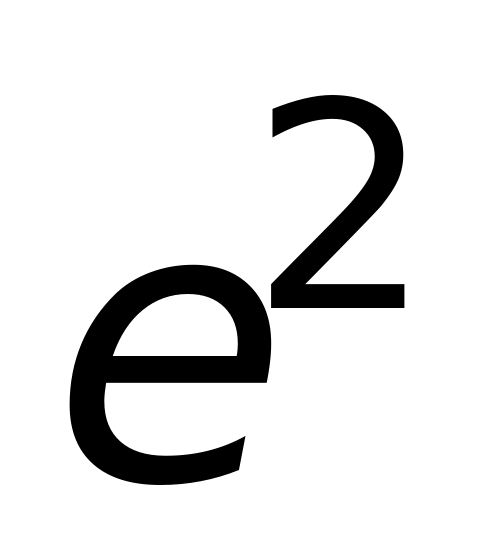 ;
в)
;
в)
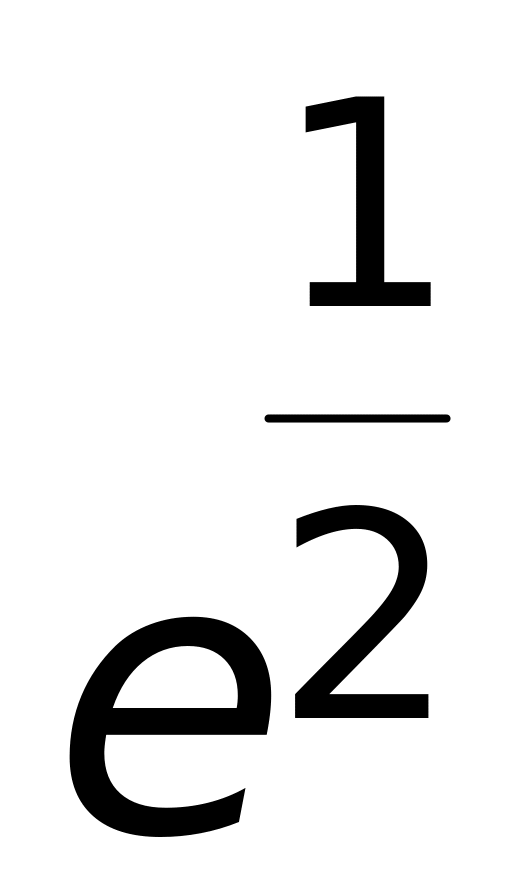 (верный ответ);
г) не существует.
(верный ответ);
г) не существует.Существует ли предел функции
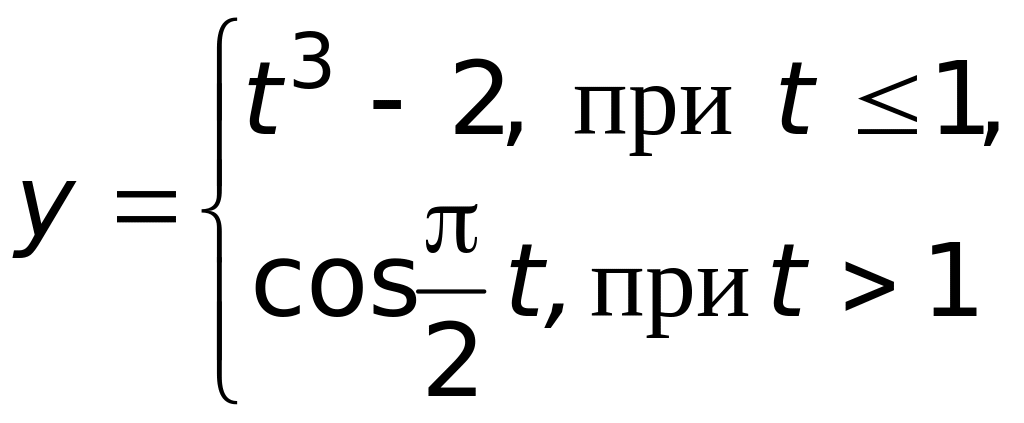 в точках
в точках
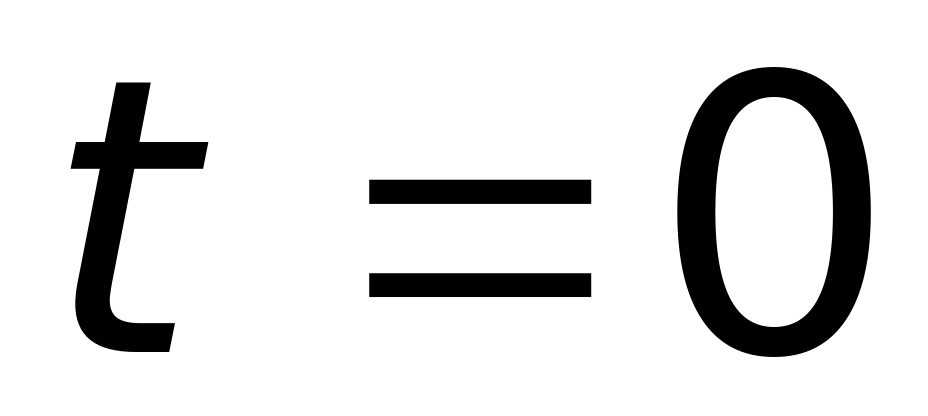 и
и
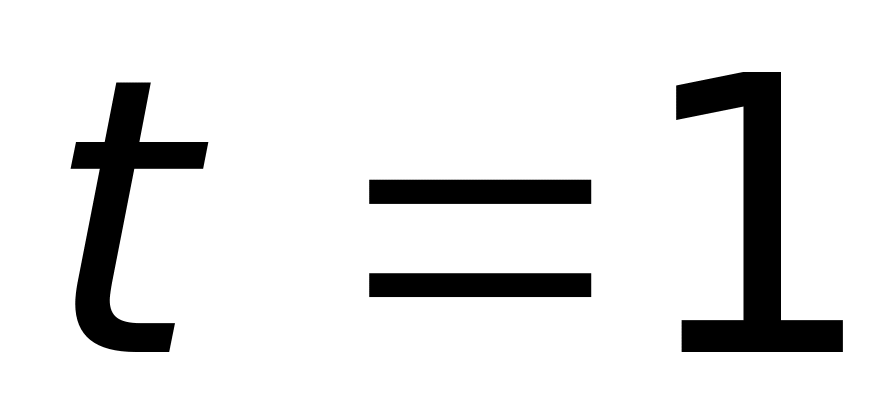 ?
Если существует, то чему равен?
Ответ:
а) в точке
существует и
?
Если существует, то чему равен?
Ответ:
а) в точке
существует и
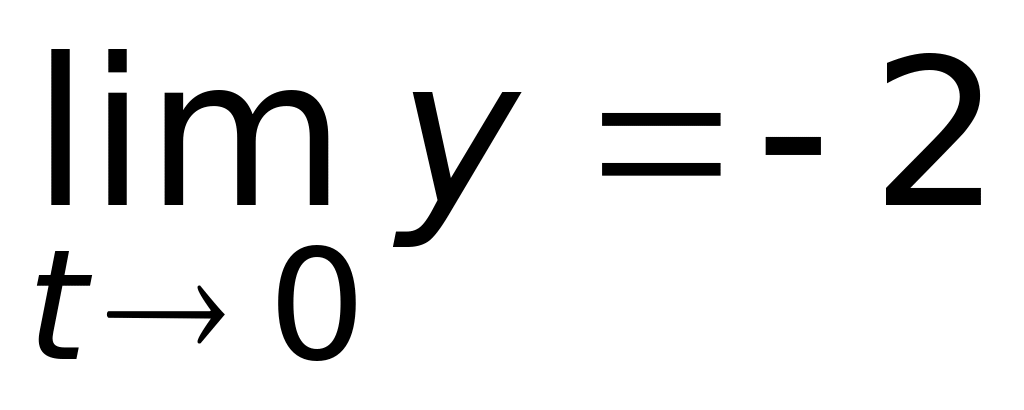 ,
в точке
не существует (верный ответ);
б) в
точках
и
пределы не существуют;
в) пределы
существуют:
;
,
в точке
не существует (верный ответ);
б) в
точках
и
пределы не существуют;
в) пределы
существуют:
;
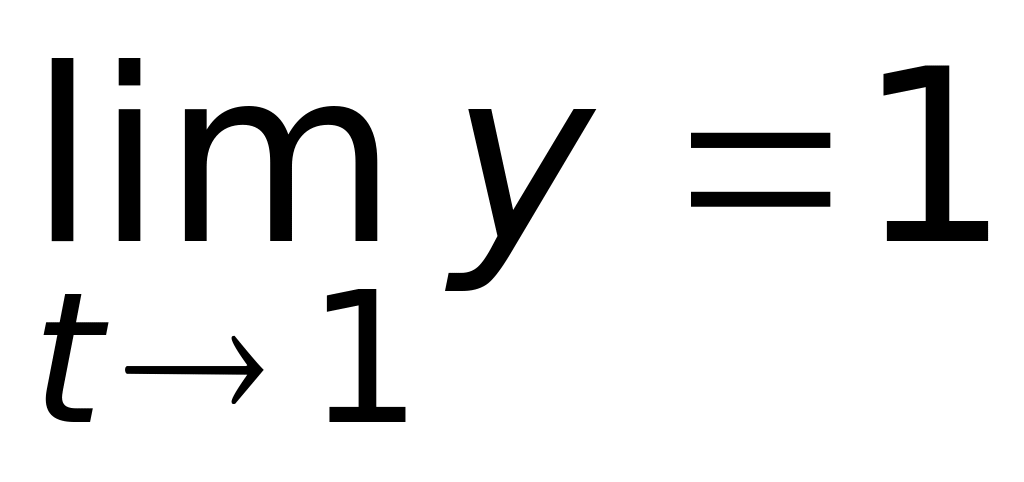 ;
г)
в точке
предел не существует, а в точке
.
;
г)
в точке
предел не существует, а в точке
.Найти точки разрыва функции
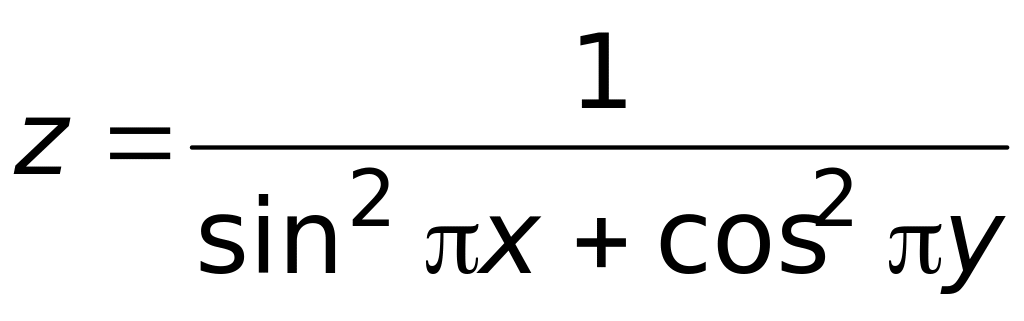 .
Ответ:
а)
.
Ответ:
а)
 ;
б)
;
б)
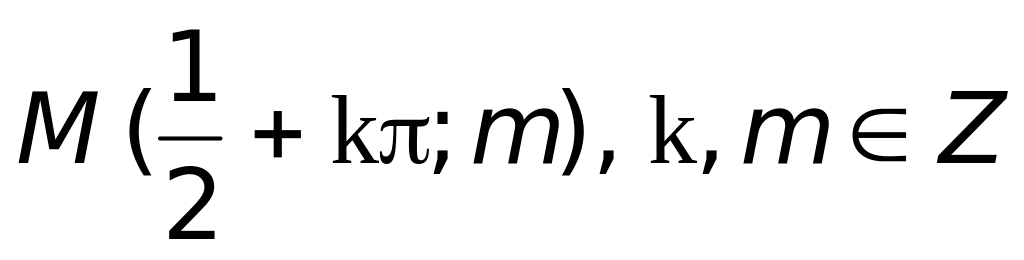 ;
в)
;
в)
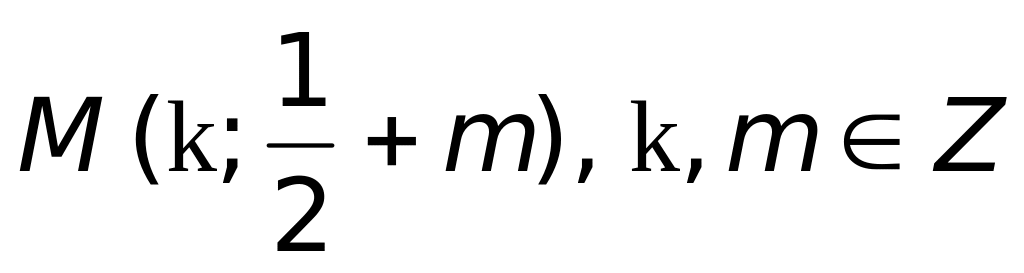 (верный
ответ);
г)
(верный
ответ);
г)
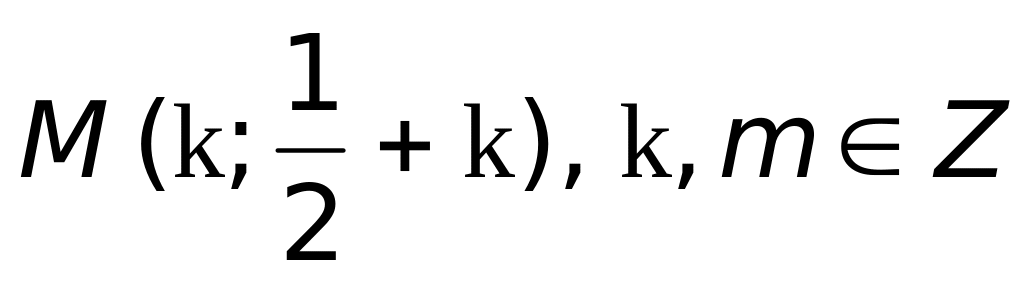 .
.
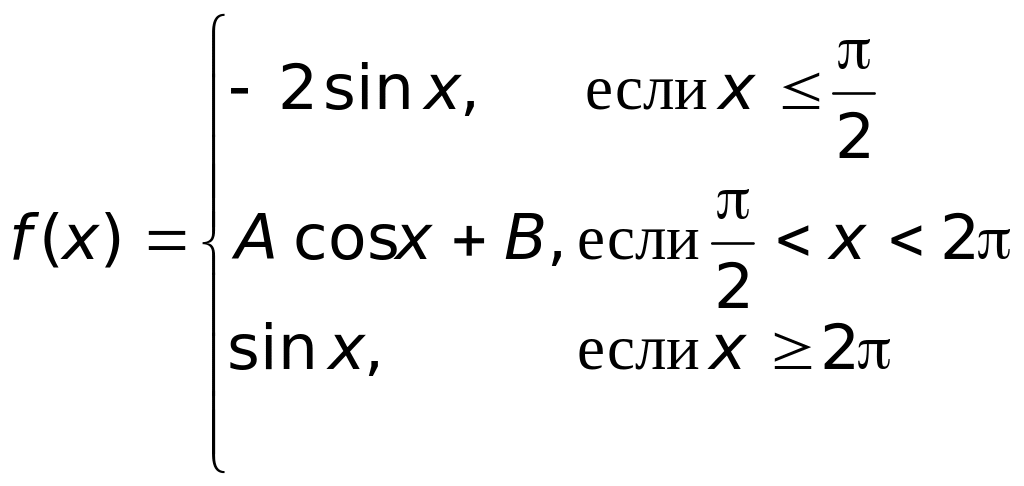 .
Найти А и В, если известно, что функция
не имеет точек разрыва.
Ответ: а) А=0,
В=1;
б) А=1, В=1;
в) А=2, В=2;
г) А=2,
В=-2(верный ответ).
.
Найти А и В, если известно, что функция
не имеет точек разрыва.
Ответ: а) А=0,
В=1;
б) А=1, В=1;
в) А=2, В=2;
г) А=2,
В=-2(верный ответ). .
Найти b,
если функция непрерывна для всех
.
Найти b,
если функция непрерывна для всех
 .
Ответ:
а) b=0;
б) b=1(верный
ответ);
в) b=-1;
г) b=-2.
.
Ответ:
а) b=0;
б) b=1(верный
ответ);
в) b=-1;
г) b=-2.Найти точки разрыва функции и определить их характер
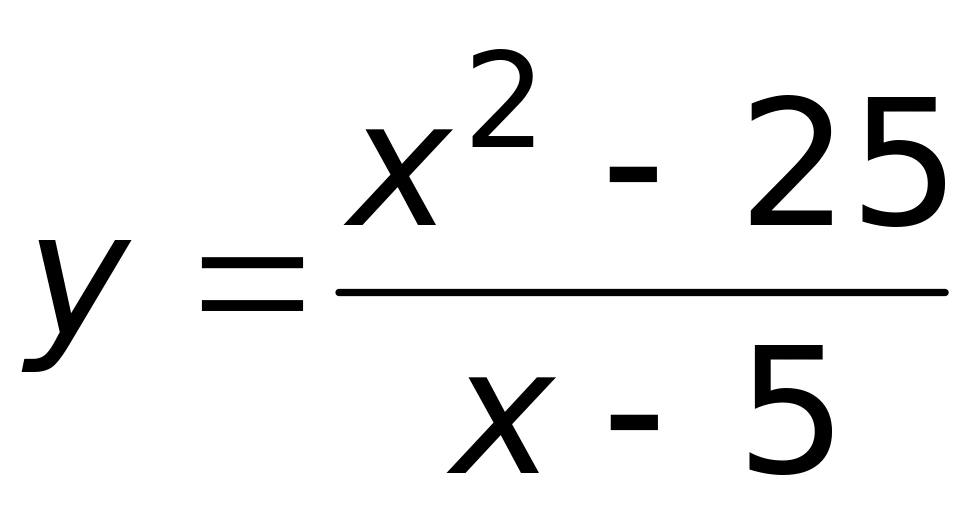 .
Ответ:
а) точка разрыва
.
Ответ:
а) точка разрыва
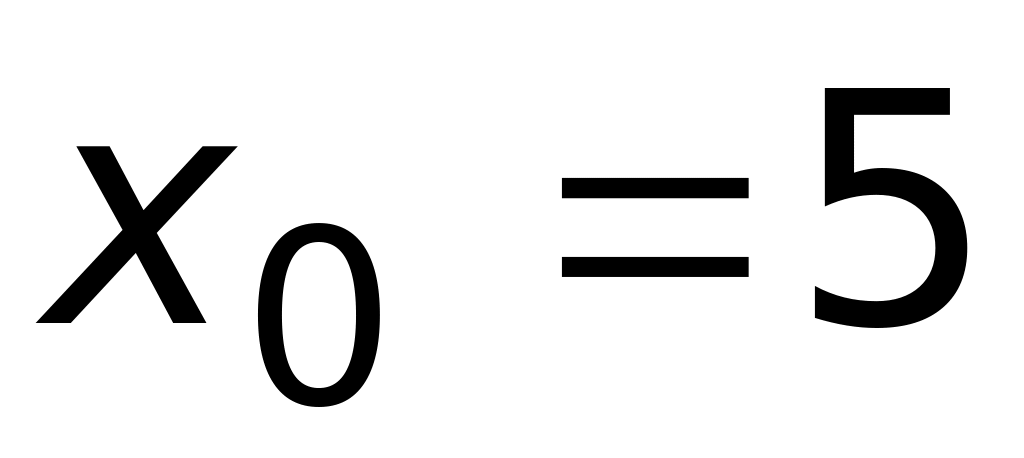 ,
устранимый разрыв(верный ответ);
б)
точка разрыва
,
разрыв первого рода с конечным скачком;
в) односторонние пределы в точке
не существуют;
г) точек разрыва
функция не имеет.
,
устранимый разрыв(верный ответ);
б)
точка разрыва
,
разрыв первого рода с конечным скачком;
в) односторонние пределы в точке
не существуют;
г) точек разрыва
функция не имеет.Функция
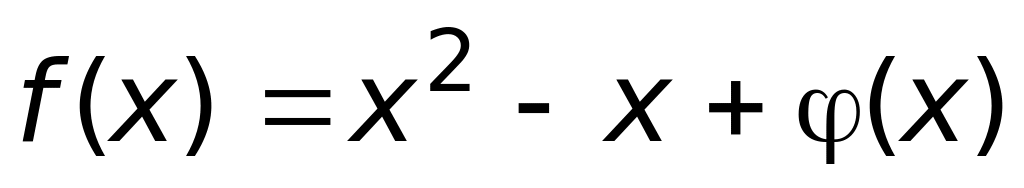 ,
где
,
где
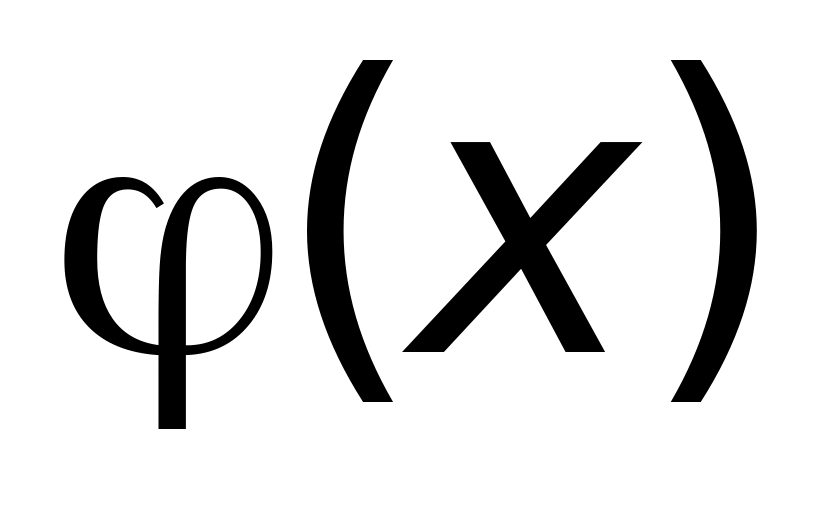 - неизвестная функция, непрерывна в
точке,
- неизвестная функция, непрерывна в
точке,
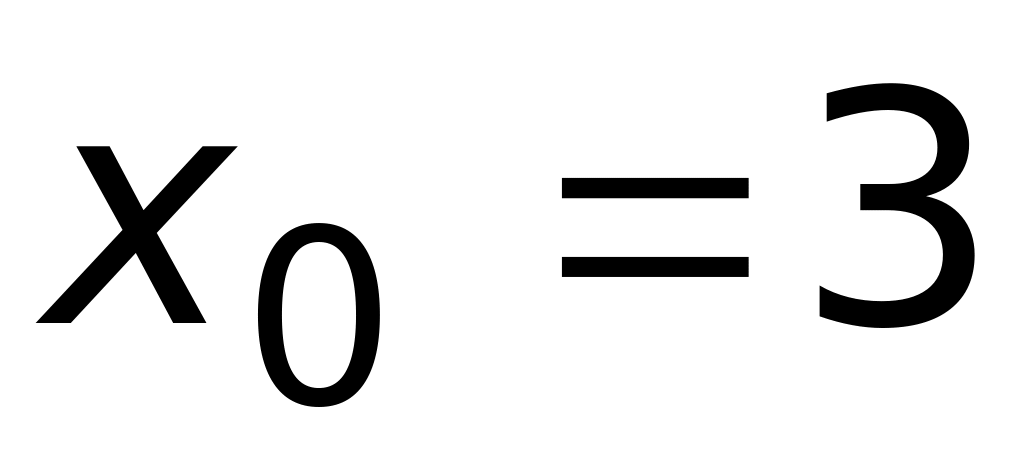 и ее
и ее
 .
Найти значения
.
Найти значения
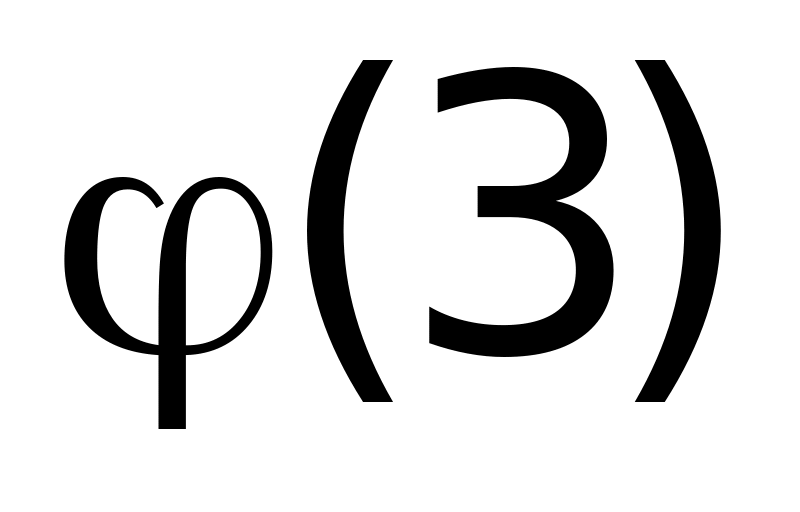 .
Ответ:
а)
.
Ответ:
а)
 ;
б)
;
б)
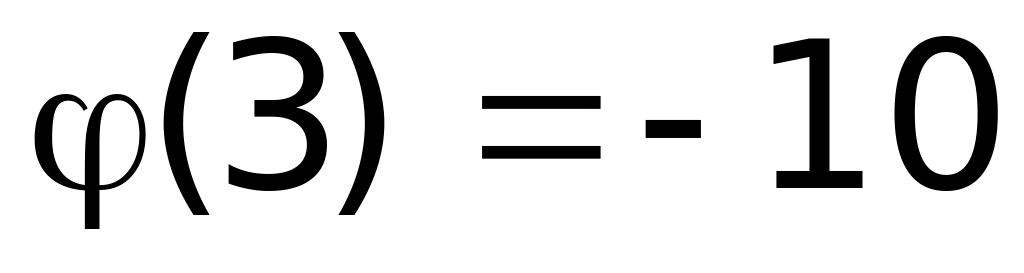 ;
в)
;
в)
 (верный ответ);
г)
(верный ответ);
г)
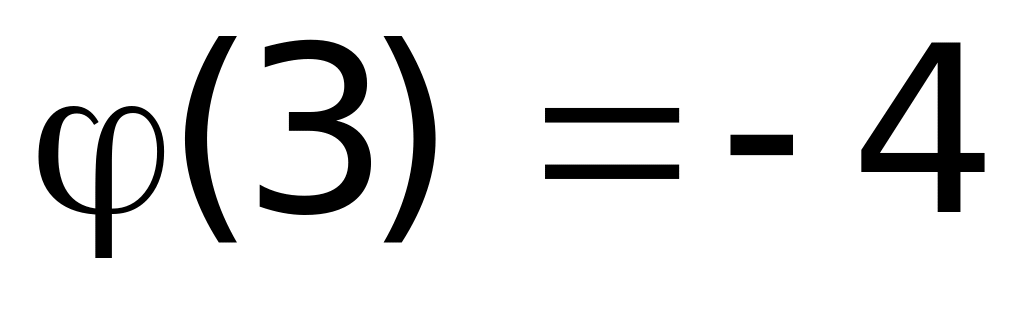 .
.Задана сходящаяся последовательность и
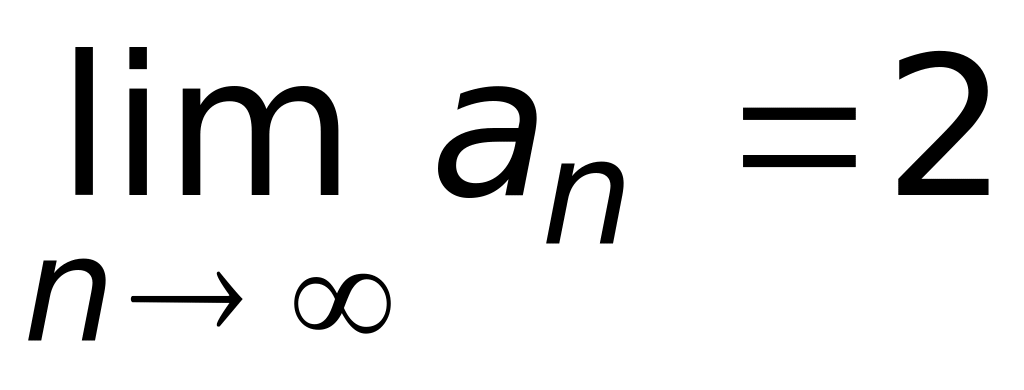 .
Найти предел
.
Найти предел
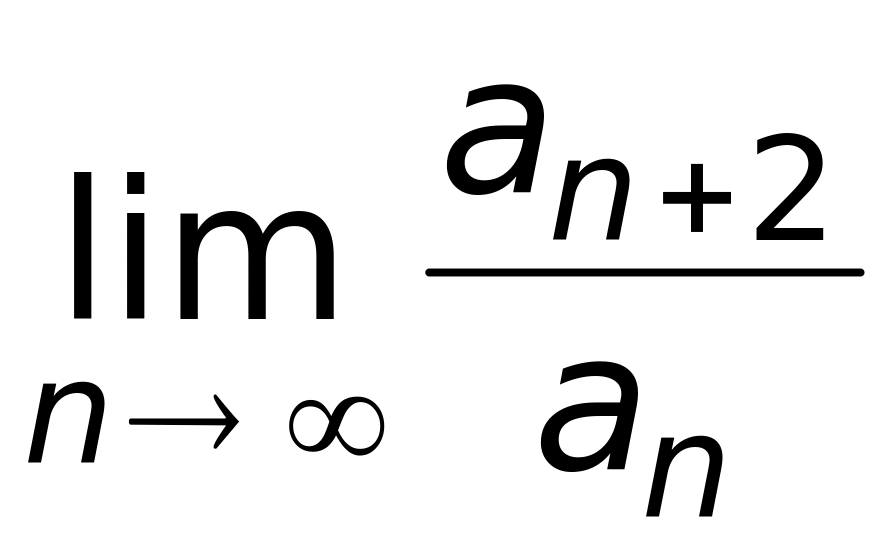 ,
если он существует.
Ответ: а) ничего
определенного сказать нельзя;
б)
,
если он существует.
Ответ: а) ничего
определенного сказать нельзя;
б)
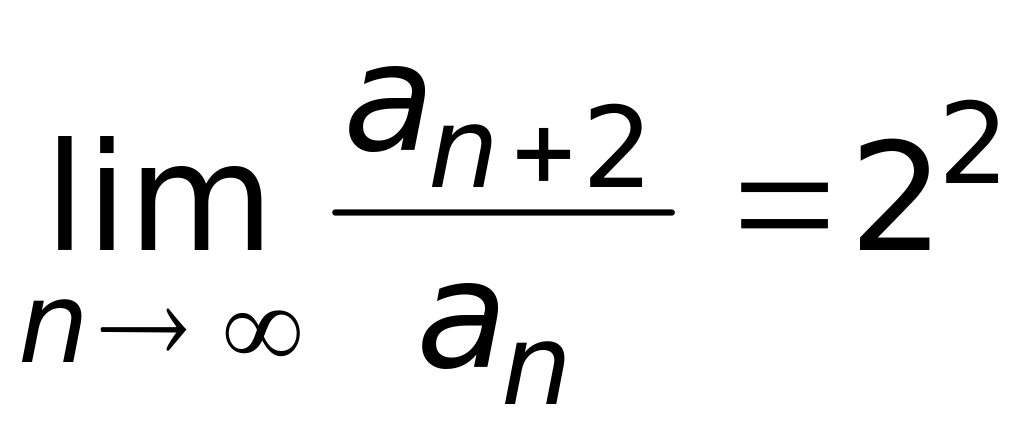 ;
в)
;
в)
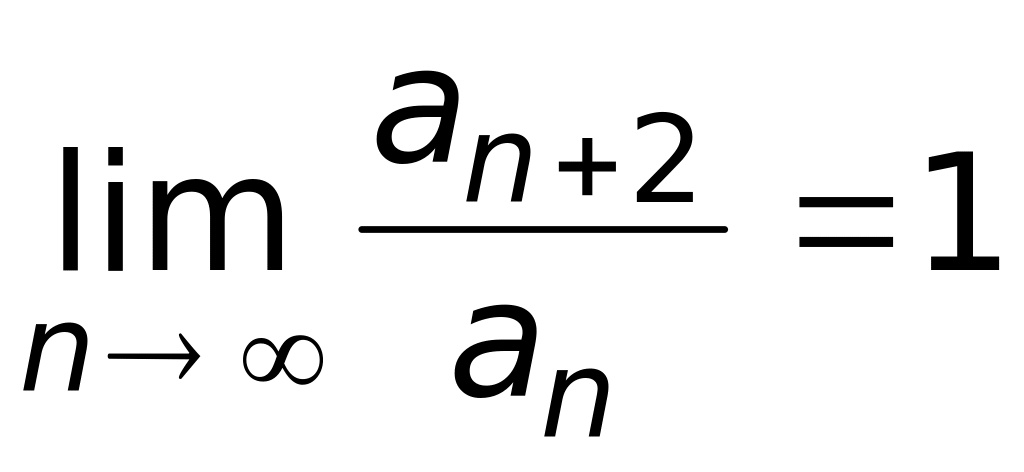 (верный
ответ);
г)
(верный
ответ);
г)
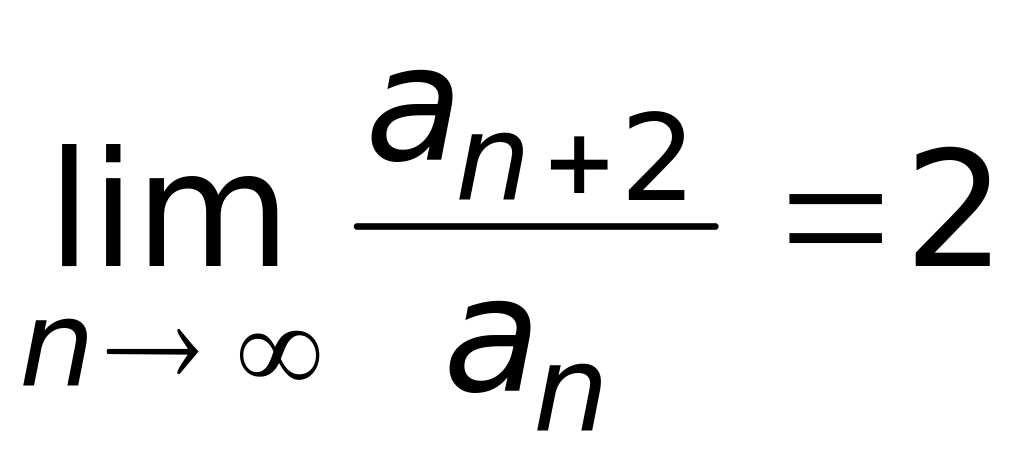 .
.Функция
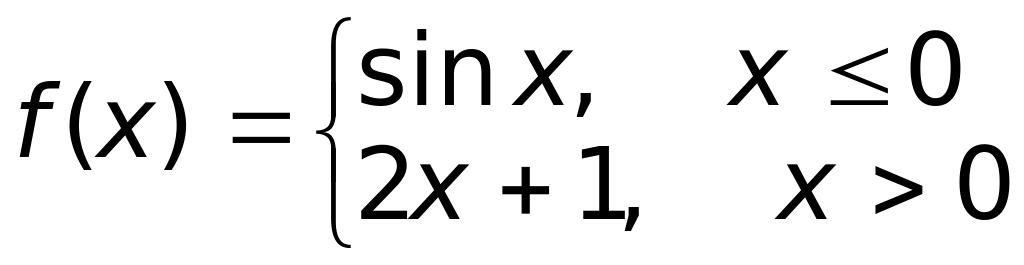 является
1) непрерывной на R;
2) непрерывной на R\{0}
(верный ответ);
3) периодической на
R;
4) ограниченной на R.
является
1) непрерывной на R;
2) непрерывной на R\{0}
(верный ответ);
3) периодической на
R;
4) ограниченной на R.Функция
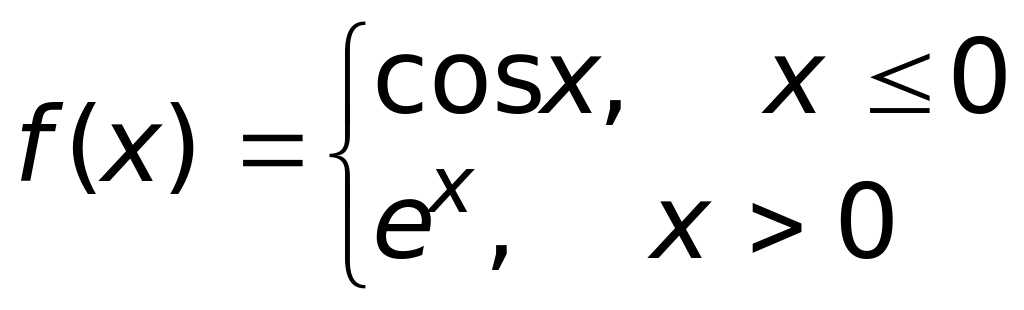 является
1) ограниченной на R;
2) периодической на R;
3) непрерывной на R
(верный
ответ);
4) монотонно убывающей на R.
является
1) ограниченной на R;
2) периодической на R;
3) непрерывной на R
(верный
ответ);
4) монотонно убывающей на R.Функция
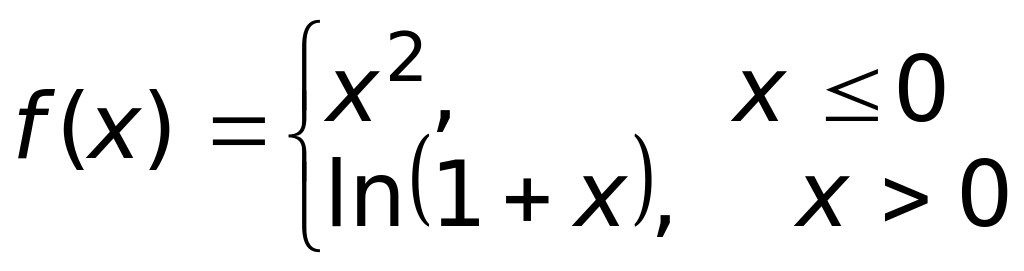 является
1) монотонно убывающей на
R;
2) ограниченной на R;
3) непрерывной на R
(верный
ответ);
4) периодической на R.
является
1) монотонно убывающей на
R;
2) ограниченной на R;
3) непрерывной на R
(верный
ответ);
4) периодической на R.Функция
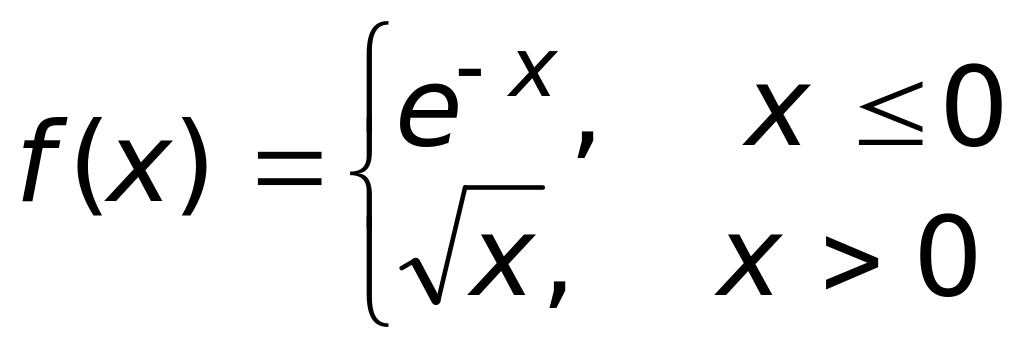 является
1) монотонно возрастающей
на R;
2) непрерывной на R;
3) ограниченной на R;
4) непрерывной на R\{0}
(верный ответ).
является
1) монотонно возрастающей
на R;
2) непрерывной на R;
3) ограниченной на R;
4) непрерывной на R\{0}
(верный ответ).Функция
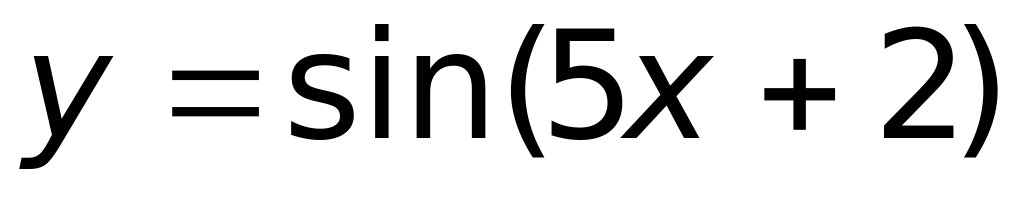 является
1) неограниченной на R;
2) периодической на R
с периодом
является
1) неограниченной на R;
2) периодической на R
с периодом
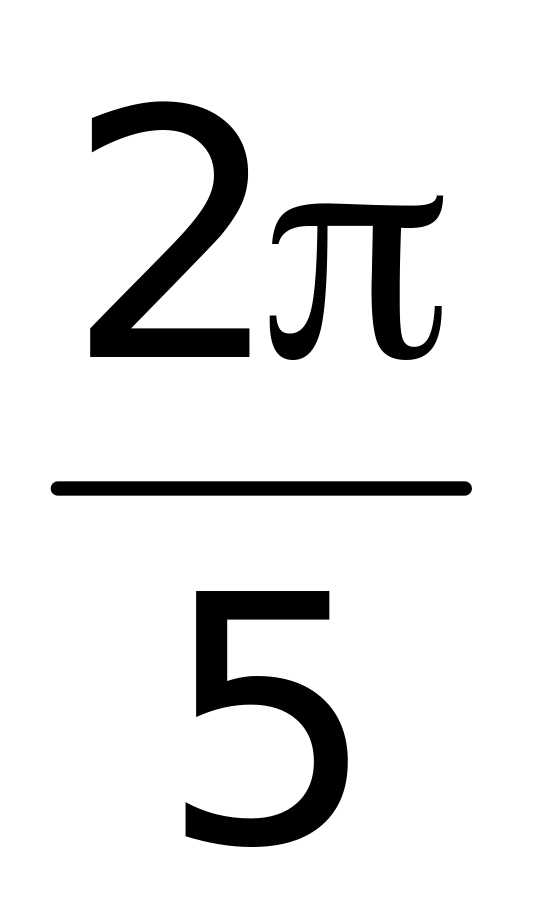 (верный ответ);
3) монотонно возрастающей
на R;
4) разрывной в точке
(верный ответ);
3) монотонно возрастающей
на R;
4) разрывной в точке
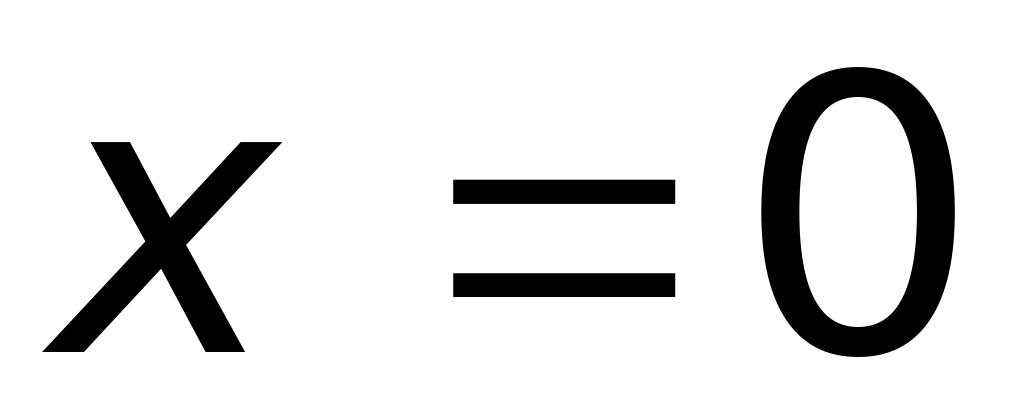 .
.Функция
 является
1) непрерывной при
является
1) непрерывной при
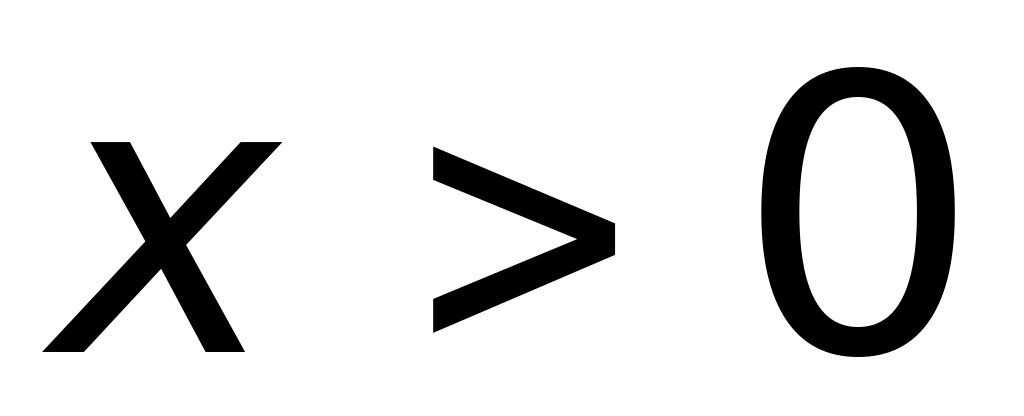 (верный ответ);
2) периодической с
периодом
(верный ответ);
2) периодической с
периодом
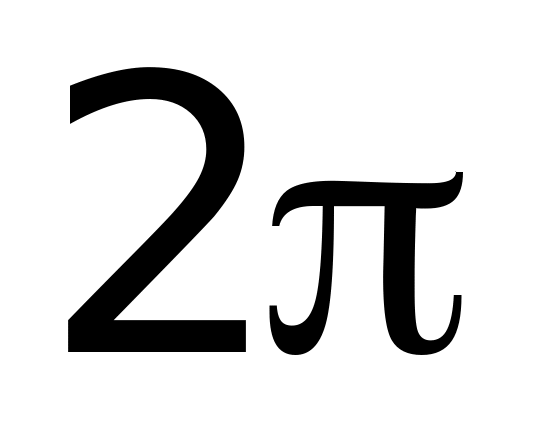 ;
3) ограниченной при
;
4) элементарной функцией при
.
;
3) ограниченной при
;
4) элементарной функцией при
.Функция
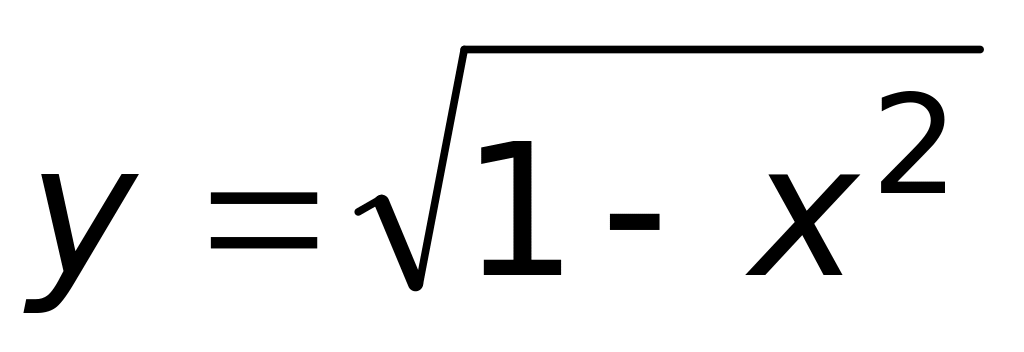 является
1) ограниченной при
является
1) ограниченной при
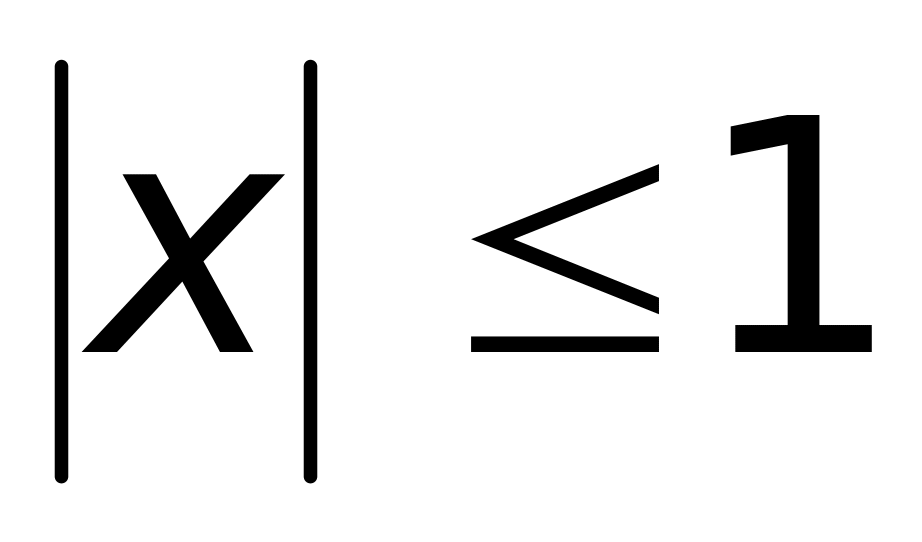 (верный ответ);
2) элементарной
функцией при
;
3) периодической функцией при
;
4) монотонно возрастающей функцией
при
(верный ответ);
2) элементарной
функцией при
;
3) периодической функцией при
;
4) монотонно возрастающей функцией
при
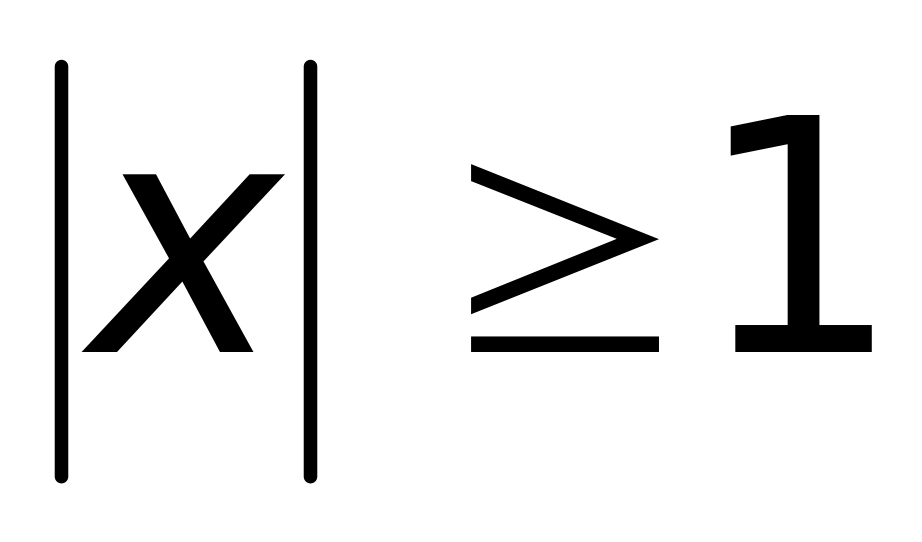 .
.Функция
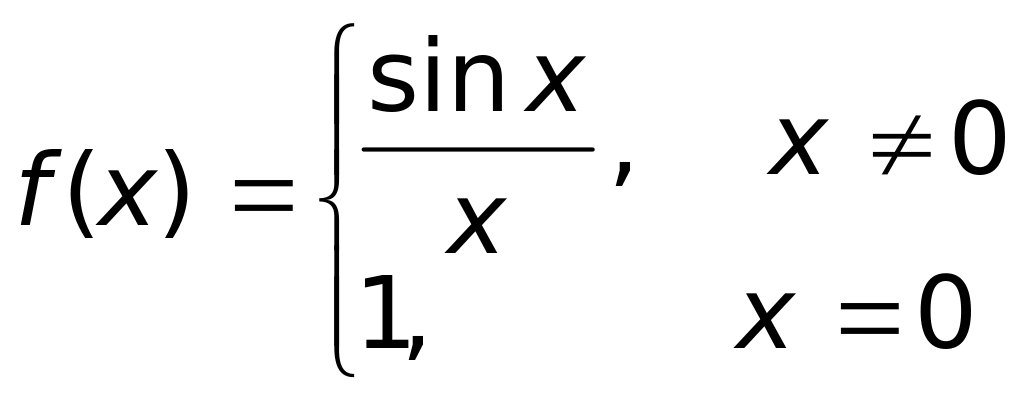 является
1) элементарной на R;
2) непрерывной на R
(верный
ответ);
3) периодической на R;
4) монотонной на R.
является
1) элементарной на R;
2) непрерывной на R
(верный
ответ);
3) периодической на R;
4) монотонной на R.Предел функции
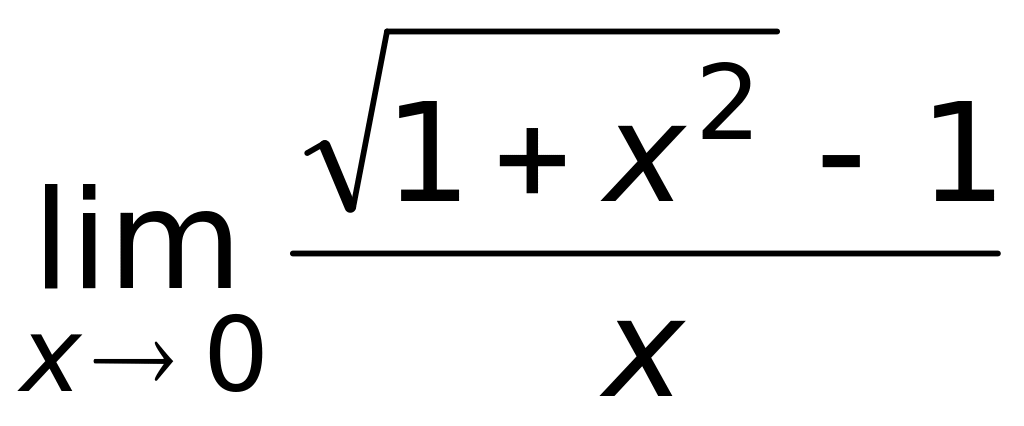 равен
1) 0 (верный ответ);
2) 2;
3)
;
4) 3.
равен
1) 0 (верный ответ);
2) 2;
3)
;
4) 3.Предел функции
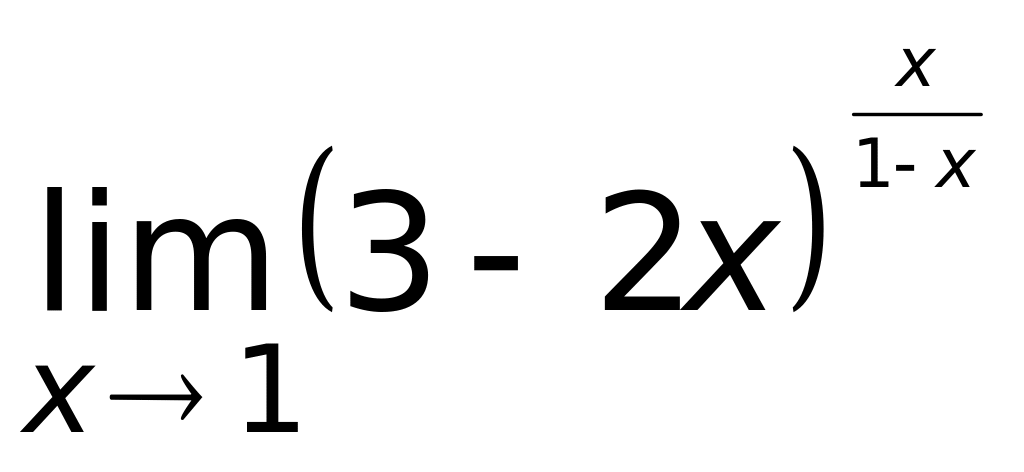 равен
1) 1;
2)
(верный ответ);
3)
;
4)
равен
1) 1;
2)
(верный ответ);
3)
;
4)
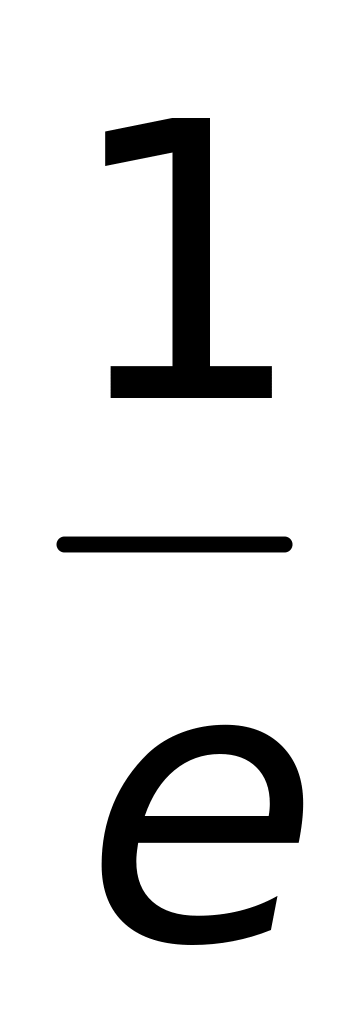 .
.Предел функции
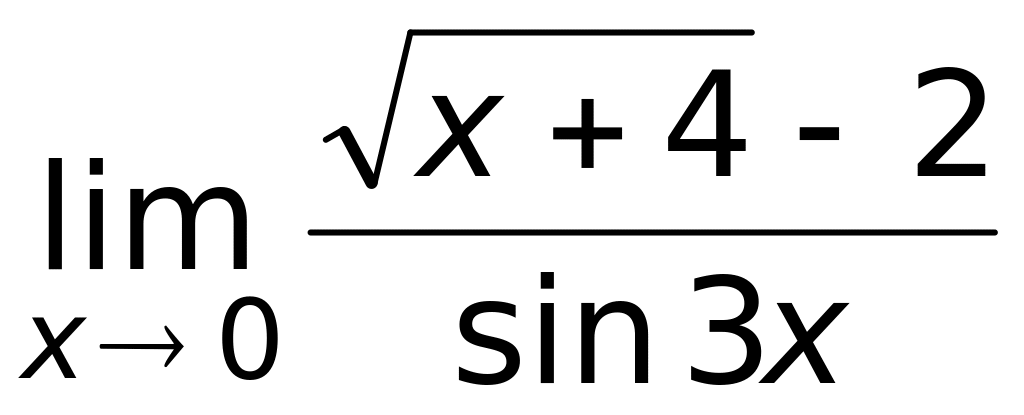 равен
1)
равен
1)
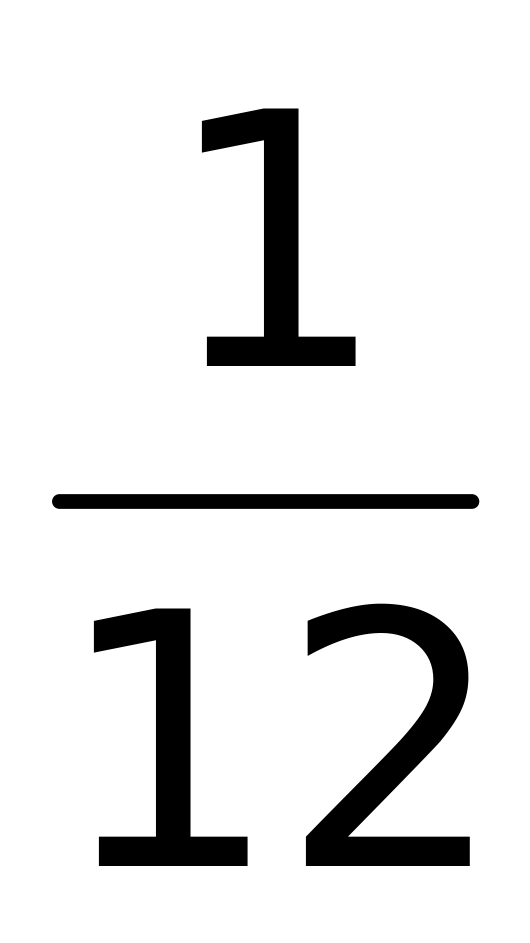 (верный ответ);
2)
(верный ответ);
2)
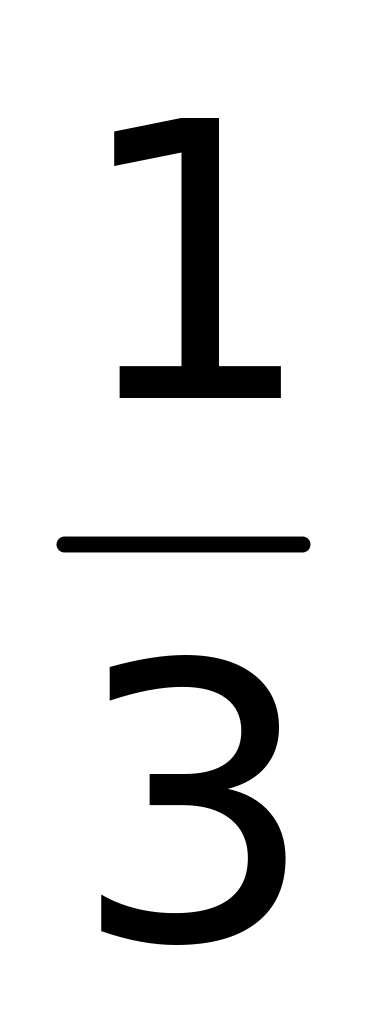 ;
3)
;
3)
 ;
4) 1.
;
4) 1.Предел функции
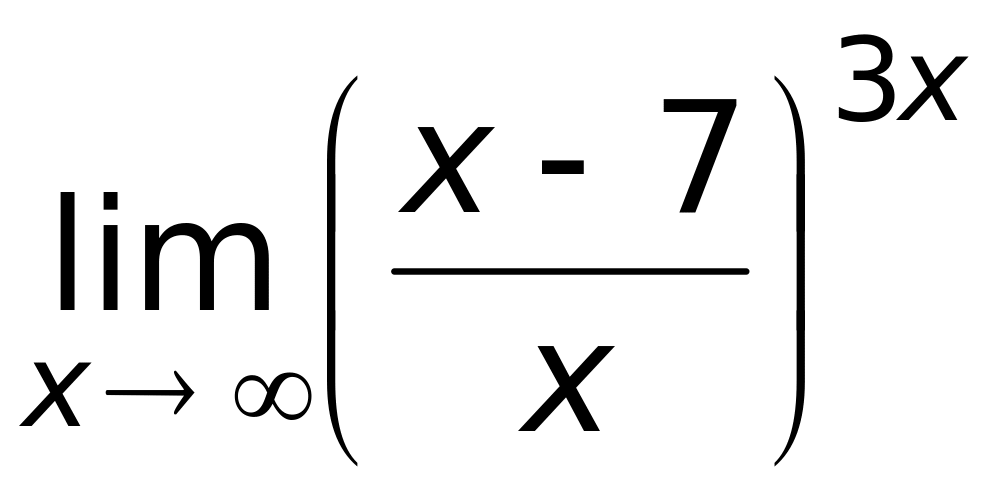 равен
1)
равен
1)
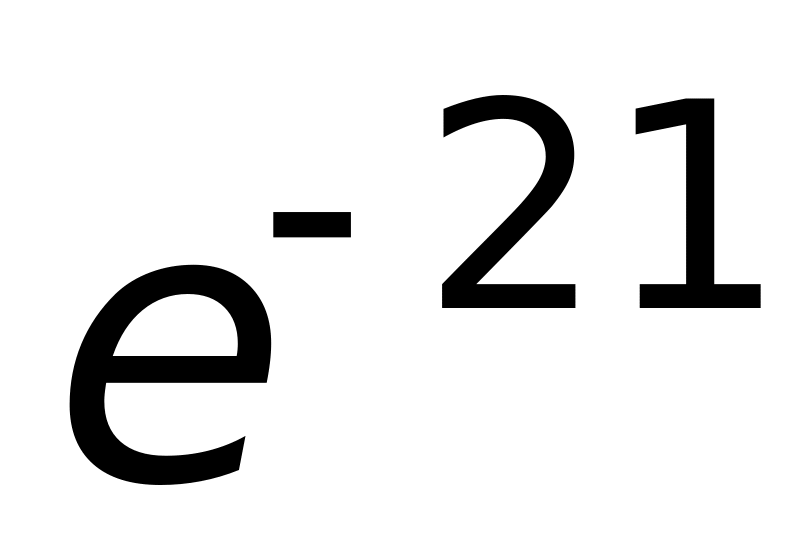 (верный ответ);
2)
;
3)
;
4)
(верный ответ);
2)
;
3)
;
4)
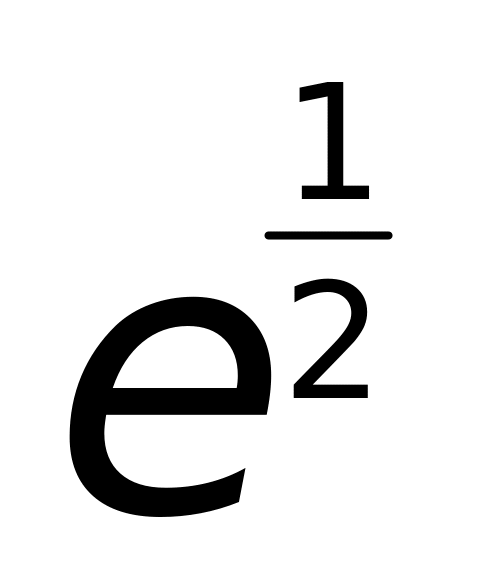 .
.Множество [1,3] является 1) неограниченным сверху; 2) неограниченным снизу; 3) ограниченным (верный ответ); 4) неограниченным и сверху и снизу.
Множество [1,+) является 1) неограниченным сверху (верный ответ); 2) ограниченным; 3) неограниченным снизу; 4) неограниченным сверху и снизу.
Точная верхняя грань множества
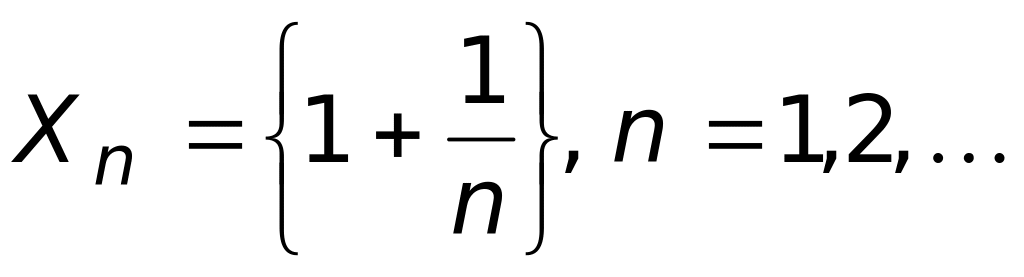 равна
1) 1;
2) 2 (верный ответ);
3)
0;
4) 3.
равна
1) 1;
2) 2 (верный ответ);
3)
0;
4) 3.Точная нижняя грань множества равна 1) 0; 2) 1 (верный ответ); 3) 2; 4) .
Точная верхняя грань множества
 равна
1) 0;
2) 1 (верный ответ);
3)
2;
4) 3.
равна
1) 0;
2) 1 (верный ответ);
3)
2;
4) 3.Точная нижняя грань множества равна 1) (верный ответ); 2) ; 3) ; 4) 0.
