3.3.1 Определение приближенной ок
Область
(множество) допустимых решений X
определяется системой ограничений
,
i
= 1, 2, 3.
Область допустимых решений в общем
случае состоит их двух подобластей
,
(3.2)
где
–
область согласия, в которой частные
критерии могут изменяться согласовано;
–
область
компромиссов, в которой хотя бы одна
пара критериев является строго
противоречивой.
Выделение
приближенной области компромиссов
сокращает область поиска решения x
и (или) упрощает формирование точной ОК
.
Суть метода выделения ПОК для выпуклого
множества альтернатив Х
состоит в следующем. На множестве
допустимых решений X
производится
оптимизация по каждому из частных
критериев
,
,
.
Полученные результаты заносятся в
табл.3.1.
Таблица 3.1 – Результаты оптимизации по частным критериям
-
\
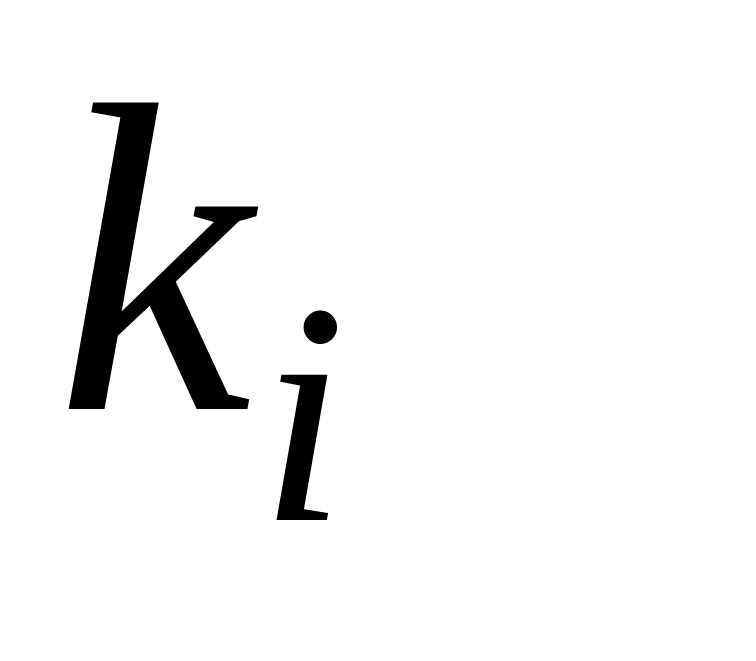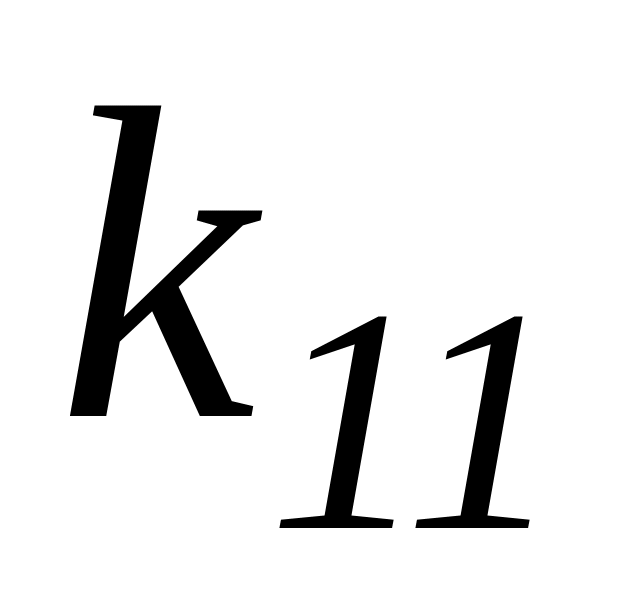
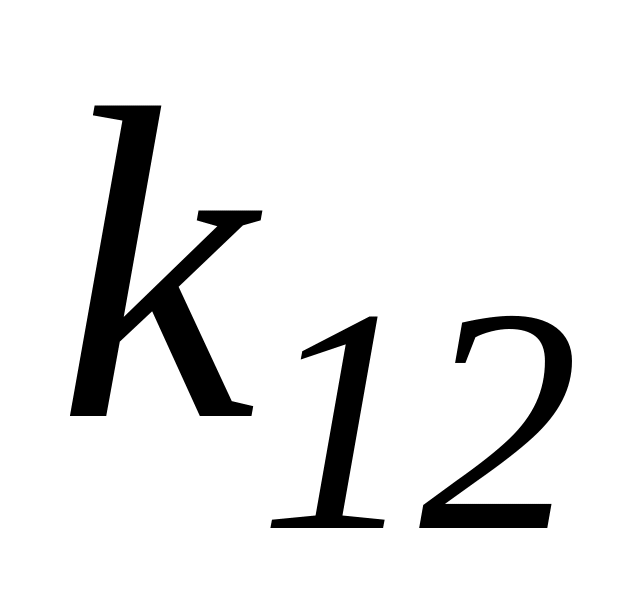
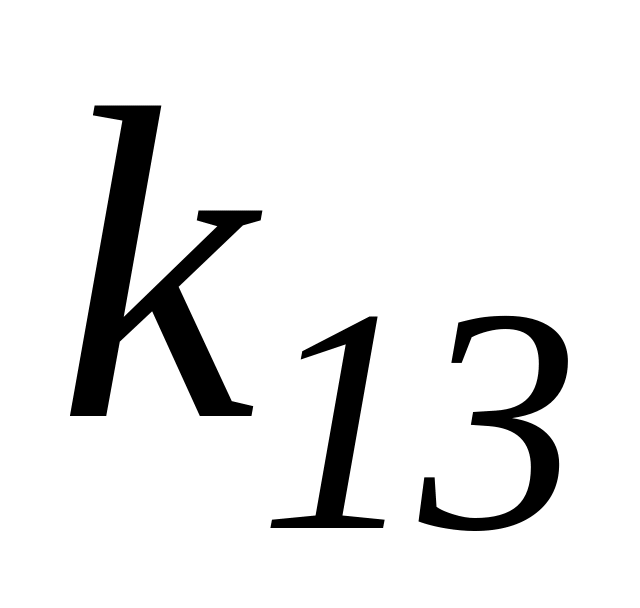
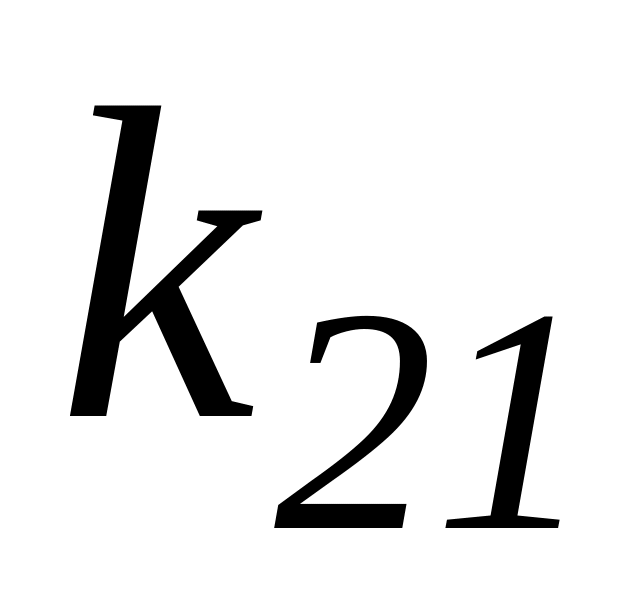
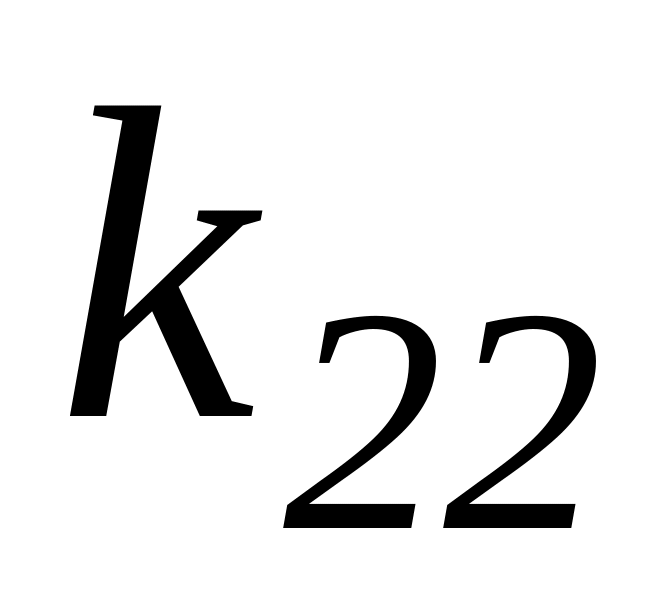
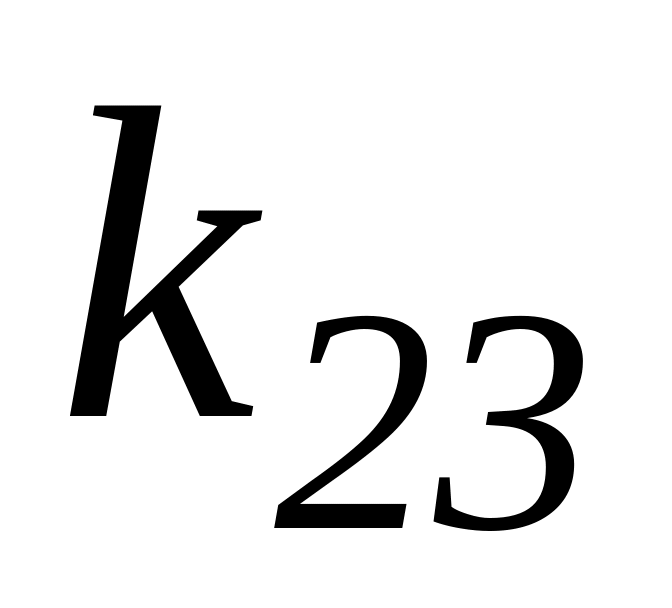
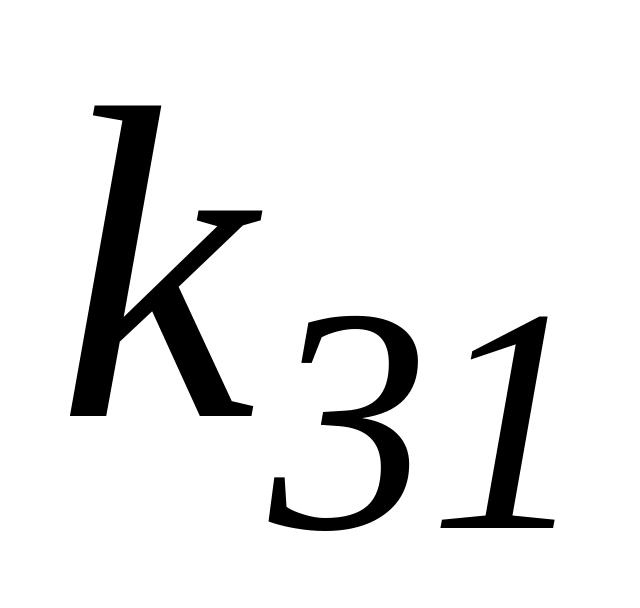
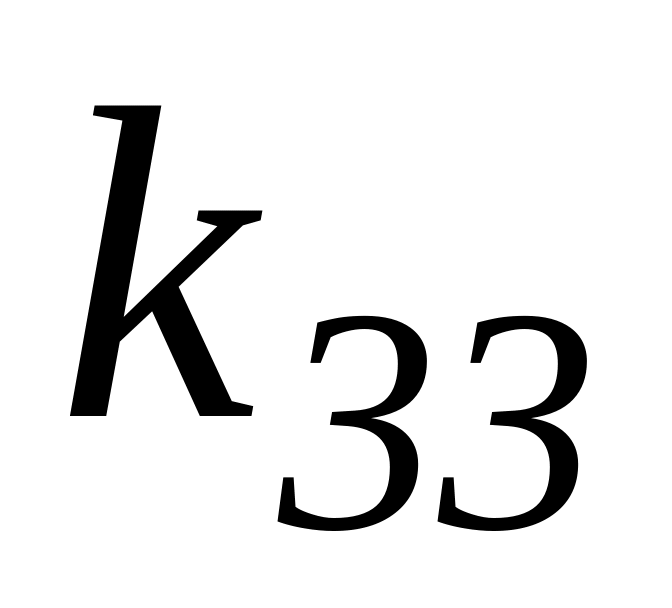
Каждая
строка табл. 3.1 содержит значения
всех частных критериев
,
полученные при оптимизации по i-му
частному критерию. Каждый из столбцов
представляет собой набор значений j-го
частного критерия в точках оптимума по
всем частным критериям. Наилучшие
значения частных критериев
= 
,
расположены на главной диагонали. Найдя
в столбцах наихудшие значения для
соответствующих частных критериев
,
,
получим границы ПОК
,
j = 1, 2, 3
в
пространстве частных критериев
.
Решения x
из
области допустимых решений X,
все частные критерии которых имеют
значения в полученных границах принадлежат
.
3.3.2 Формирование ок
В
общем случае приближенная область
компромиссов
содержит подмножество решений из области
согласия
.
Если решение x
из
может быть улучшено по одному или
нескольким частным критериям без
ухудшения качества по другим, то оно не
включается в
.
Пусть решения
принадлежат
.
Область компромиссов
содержит
только неулучшаемые по частным критериям
решения. Алгоритм формирования ОК
состоит в сравнении всевозможных пар
решений
,
т.е.
и
,
и
,…,
и
,
и
,…
и т.д. и удалении из дальнейшего
рассмотрения решений, которые по всем
частным критериям хуже других (другого).
3.3.3 Функции полезности частных критериев
Частные
критерии
,
,
посредством которых оцениваются решения,
во-первых, являются противоречивыми,
во-вторых, имеют различные физический
смысл, размерность и интервал изменения.
Оценку ценности решения по каждому из
критериев в работе рекомендуется
производить с помощью ФП вида
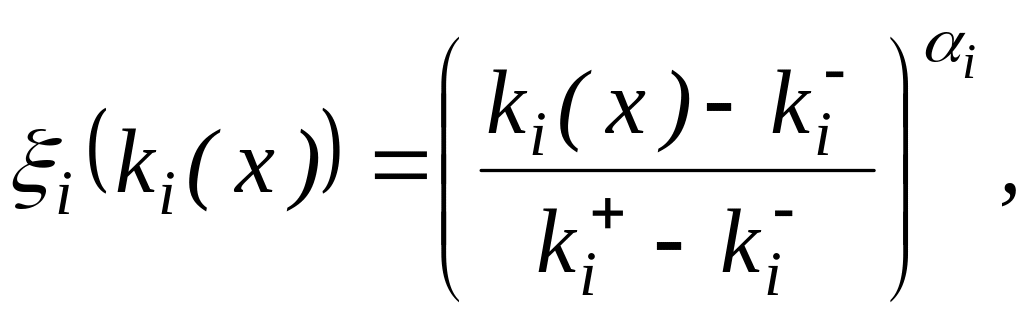(3.3)
или функции потери полезности
(3.4)
где
-
коэффициент нелинейности; при
=
1 получаем линейную, при 0 <
<
1 - выпуклую, при
>
1 - вогнутую зависимости от значения
критерия.
ФП такого вида может рассматриваться как функция принадлежности решений размытому (нечеткому) множеству "лучший вариант".