1.10.7. Средняя и предельная ошибки выборочного среднего

Ошибкой выборочного среднего или ошибкой выборки называется абсолютная величина разности генерального и выборочного средних. Так как генеральное среднее неизвестно, ошибку выборки вычислить нельзя, но ее можно оценить с помощью предельной ошибки:

, (1.10.15)

где

 предельная ошибка выборки;

 средняя ошибка, вычисляемая по формуле, зависящей от вида выборки;

 доверительный коэффициент, значение которого находится по заданной вероятности р в специальных таблицах.

Доверительный интервал, в котором с вероятностью р находится генеральное среднее, имеет вид:

. (1.10.16)

Средняя ошибка малой выборки вычисляется по формуле

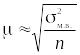, (1.10.17)

где дисперсия малой выборки, вычисляемая по формуле

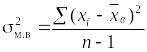. (1.10.18)

Предельная ошибка малой выборки вычисляется по формуле (1.10.15), где коэффициент находится по уровню значимости и числу в табл. П4.

Пример 1.10.4. При проверке качества партии колбасы получены следующие данные о процентном содержании поваренной соли в 10 пробах: 4,3; 4,2; 3,8; 4,3; 3,7; 3,9; 4,5; 4,4; 4,0; 3,9. Найдем с вероятностью 0,95 границы, в которых находится средний процент содержания поваренной соли в партии колбасы.

Составим расчётную табл. 1.10.10. По суммам в итоговой строке табл. 1.10.10 вычислим выборочную среднюю, выборочную дисперсию и среднюю ошибку выборки:

, ,

.

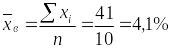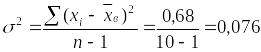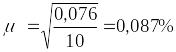Таблица 1.10.10

Расчетные показатели

i	(%)
1	4,3	0,2	0,04
2	4,2	0,1	0,01
3	3,8	0,3	0,09
4	4,3	0,2	0,04
5	3,7	– 0,4	0,16
6	3,9	– 0,2	0,04
7	4,5	0,4	0,16
8	4,4	0,3	0,09
9	4,0	–0,1	0,01
10	3,9	– 0,2	0,04
	41,0		0,68

В табл. П4 по уровню значимости и числу находим доверительный коэффициент: =2,262. Вычислим предельную ошибку выборки: . Найдем доверительный интервал (1.10.16):

или .

Таким образом, с вероятностью 0,95 можно утверждать, что в партии колбасы содержание поваренной соли находится в пределах от 3,9% до 4,3%.

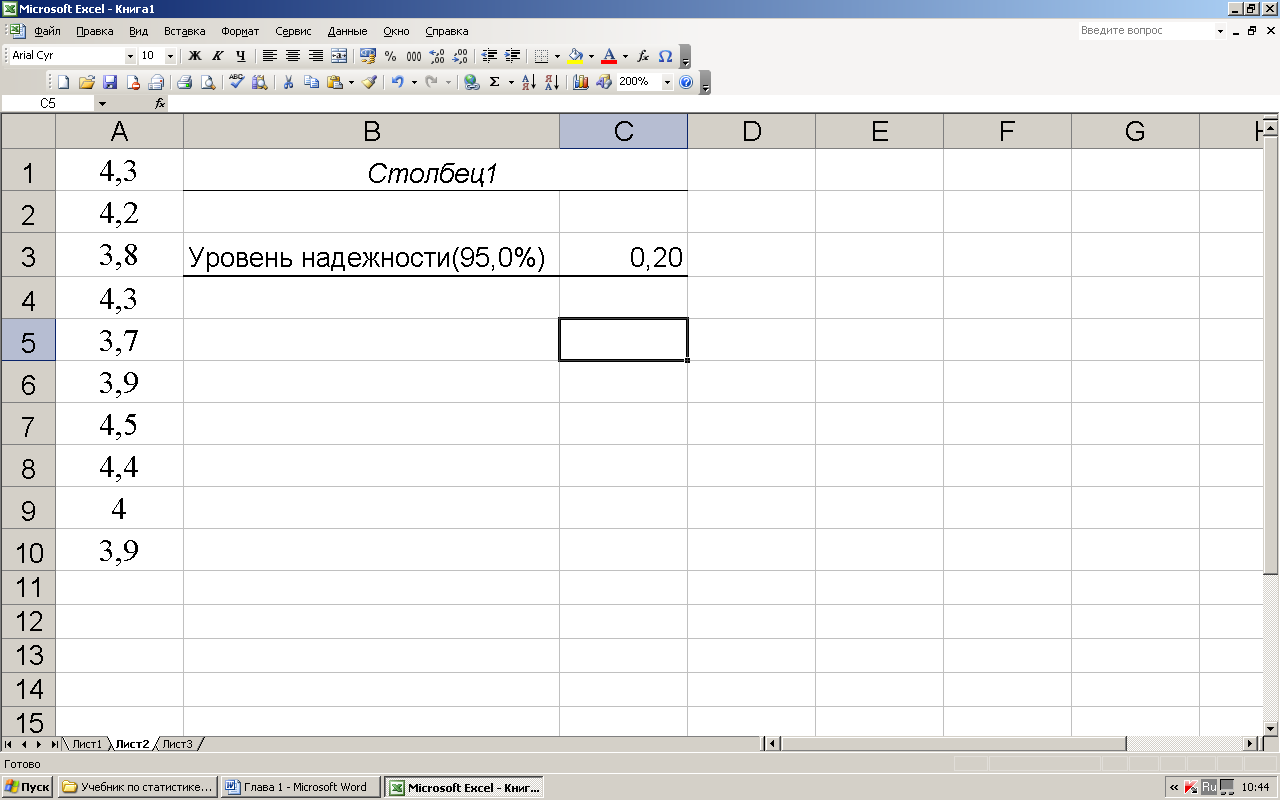
1.10.6. Вычисление предельной ошибки (пример 1.10.4)

Предельную ошибку малой выборки можно найти, применяя Excel (рис. 1.10.6). Для этого надо:

1) в столбце ячеек записать выборку;

2) в меню СЕРВИС выбрать ОПИСАТЕЛЬНАЯ СТАТИСТИКА;

3) указать уровень надежности (доверительную вероятность);

4) снять остальные флажки, указать ячейку выходного интервала и выбрать ОК.

Упражнение 1.10.7. Отобрано 10 рабочих цеха для определения среднего времени выполнения определенной операции рабочими цеха. Выборочное среднее время оказалось равным 10,4 мин, а выборочное среднеквадратическое отклонение – 2 мин. Найдите границы, в которых с вероятностью 0,99 находится генеральная средняя.

Приведем следующие формулы для вычисления средней ошибки  большой выборки ( ):

1) средняя ошибка  случайной повторной или бесповторной выборки вычисляется соответственно по формуле

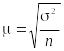или 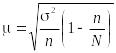; (1.10.19)

2) средняя ошибка  типической повторной или бесповторной выборки вычисляется соответственно по формуле

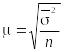или 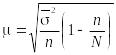, (1.10.20)

где – средняя генеральных групповых дисперсий;

3) средняя ошибка  серийной повторной или бесповторной выборки вычисляется соответственно по формуле

или 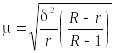, (1.10.21)

где – генеральная межгрупповая (межсерийная) дисперсия;

r и R  число серий соответственно в выборке и в генеральной совокупности.

Генеральная дисперсия связана с выборочной дисперсией соотношением

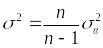. (1.10.22)

При больших значениях n генеральная дисперсия приближенно равна выборочной дисперсии.

Предельная ошибка большой выборки вычисляется по формуле (1.10.15), где коэффициент определяется из соотношения .

Напомним, что выборочное среднее значение альтернативного признака равно выборочной доле единиц в выборке, обладающих этим признаком ( ), а выборочная дисперсия равна произведению .

Пример 1.10.5. При проверке качества хлебобулочных изделий проведено 5%-е выборочное обследование партии нарезных батонов. Из 100 отобранных в выборку батонов 90 батонов оказались стандартными. Средний вес одного батона в выборке составил 500,5 г при среднеквадратическом отклонении 15,4 г. Найдем с вероятностью 0,95 доверительные интервалы для доли стандартных батанов и среднего веса одного батона во всей партии.

По условию выборочная доля:

.

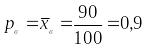Было проведено 5%-е выборочное обследование, следовательно, во всей партии  2000 батонов. Так как выборка бесповторная механическая или случайная, средняя ошибка выборочной доли равна:

.

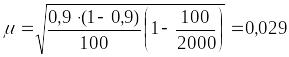Из соотношения , используя табл. П2, найдем доверительный коэффициент: .

Вычислим предельную ошибку: .

Найдем доверительный интервал (1.10.16):

или .

Таким образом, с вероятностью 0,95 можно утверждать, что доля стандартных батонов во всей партии батонов находится в интервале от 0,84 до 0,96.

Вычислим среднюю и предельную ошибки выборочного среднего веса одного батона:

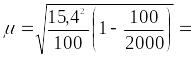1,5 и .

Найдем доверительный интервал (1.10.16):

или .

Таким образом, с вероятностью 0,95 можно утверждать, что средний вес одного батона во всей партии батонов находится в интервале от 497,6 г до 503,4 г.

Упражнение 1.10.8. Дано распределение пачек чая по весу в выборке из партии чая (табл. 1.10.11).

Таблица 1.10.11