Распределение предприятий по товарной продукции в оптовых ценах

Интервалы товарной продукции, млн. руб.	Число предприятий –	Середины интервалов –
А	1	2
3,6–7,2	3	5,4
5,7–13,2	4	10,2
13,2–18,0	5	15,6
18,0–22,8	6	20,4
22,8–27,6	2	25,2
	20

Для вычисления середин интервалов полученного ряда распре-деления с помощью Excel надо (рис. 1.5.3):

1. в ячейки А1-А5 записать левые границы интервалов;

2. в ячейки В1-В5 записать правые границы интервалов;

3. в ячейку С1 записать формулу =(А1+В1)/2 и нажать клавишу Enter;

4. подвести курсор к нижнему правому углу ячейки С1 до появления знака «+» и, нажав левую кнопку мыши, растянуть рамку на ячейки С1-С5 , затем отпустить кнопку (в ячейках С1-С5 будут записаны середины интервалов);

Рис. 1.5.3. Середины интервалов товарной

продукции предприятий

Записывая интервалы, соответствующие частоты и середины интервалов в табл. 1.5.4, получим интервальный ряд распределения предприятий по товарной продукции (гр. А и 1) и соответствующий ему дискретный ряд (гр. 2 и 1).

1.5.2. Графическое изображение рядов распределения

Для наглядности дискретный или атрибутивный ряд изобра-жается в виде графика, который называется полигоном.

Для построения полигона дискретного или атрибутивного ряда надо на координатной плоскости построить точки с координатами , где первая координата x_i равна соответственно варианте количественного признака или порядковому номеру атрибутивного признака, а вторая координата y_i равна соответствующей частоте, либо относительной частоте.

Полигон, построенный по частотам или относительным частотам, называется соответственно полигоном частот или полигоном относительных частот.

Полигон удобно строить, применяя Excel. Например, для построения полигона частот распределения пар обуви по их размерам (пример 1.5.1), изображенного на рис. 1.5.4, надо:

1. в ячейки A1-А8 записать варианты 37, 38, 39, 40, 41, 42, 43, 44;

2. в ячейки В1-В8 записать частоты 1, 4, 5, 9, 10, 7, 2, 2;

3. в меню Вставка выбрать Диаграмма;

4. выбрать График с маркерами и Далее;

5. выбрать Диапазон;

6. выделить ячейки В1-В8;

7. выбрать Ряды в столбцах и Далее;

8. выбрать Ряд, поставить курсор в рамку Подписи оси Х;

9. выделить ячейки А1-А8 и выбрать Далее;

10. выбрать Заголовки; в рамке Название диаграммы написать Распределение пар обуви по размерам, в рамке Ось Х написать Размеры обуви, в рамке Ось Y написать Количество пар обуви;

11. выбрав Линии сетки, указать Основные линии оси Х и Основные линии оси Y, выбрать Далее и Готово;

12. поставить курсор в рамку Ряд1, нажать правую кнопку «мыши» и выбрать Очистить;

13. курсор поставить в поле графика (закрашенная часть), нажать правую кнопку «мыши» и выбрать Очистить.

Рис. 1.5.4. Полигон распределения пар обуви по размерам

Заметим, что при изменении значений входного параметра (размера обуви) полигон перестраивается автоматически.

Аналогично строится полигон атрибутивного ряда распределе-ния, представленного в табл. 1.5.2 (рис. 1.5.5).

Для наглядности интервальный ряд изображается в виде графика, называемого гистограммой. Для построения гистограммы интерваль-ного ряда надо отложить интервалы на горизонтальной оси системы координат и на них как на основаниях построить прямоугольники, высоты которых равны соответствующим частотам, либо относитель-ным частотам. Гистограмма, построенная по частотам или относительным частотам, называется соответственно гистограммой частот или гистограммой относительных частот.

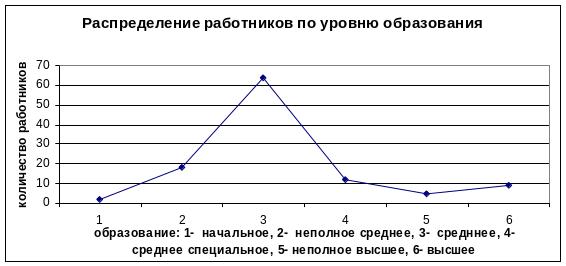
Рис. 1.5.5. Полигон распределения работников предприятия по

уровню образования

При построении гистограммы интервального ряда с неравными по длине интервалами высоты прямоугольников иногда берутся равными плотностям распределения – отношениям частот к длинам интервалов. При таком выборе высот прямоугольников их площади пропорциональны частотам.

Гистограмму интервального ряда с равными по длине интервалами удобно строить, применяя Excel .

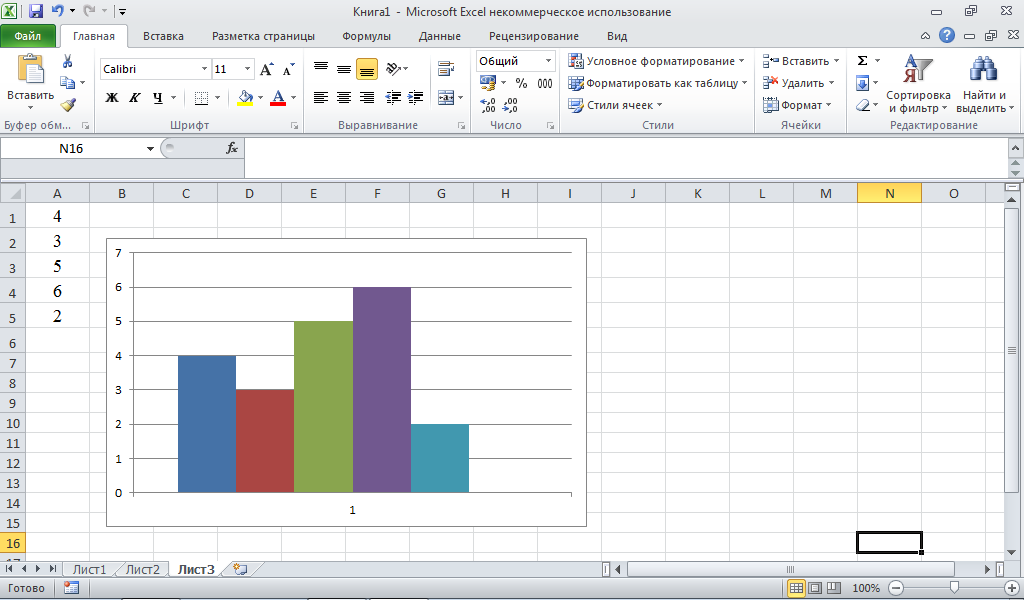
Рис. 1.5.6. Гистограмма распределения

предприятий по товарной продукции, млн. руб.

Например, для построения гистограммы частот интервального ряда (рис. 1.5.6), представленного в табл. 1.5.3, надо:

1) в ячейки A1-A5 записать частоты;

2. в меню Вставка выбрать Диаграмма;

3. выбрать Гистограмма и Далее;

4. выбрать Диапазон данных, выделить ячейки A1-A5 и ОК.

5. нажать правую кнопку мыши, поставить курсор в прямоугольник Выбрать данные, нажать кнопку Строка/столбец и ОК.

6. удалить надпись ряд 1, ряд 2

Упражнение 1.5.1. В результате статистического наблюдения были получены данные о ценах акций 30 предприятий, руб.:

2092, 1898, 644, 3090, 2512, 8977, 2220, 1021, 4974, 5300, 2370, 1220, 3700, 81,20, 4775, 690, 825, 667, 2984, 7805, 7350, 3742, 4750, 982, 1116, 2133, 4760, 5855, 3242, 4108.

Составьте интервальный ряд распределения предприятий по ценам акций и ему соответствующий дискретный ряд, постройте гистограмму полученного интервального ряда и полигон частот соответствующего ему дискретного ряда.

Тест 1.5.

1. Для распределения видов юридической помощи (устные советы, составление документов, поручения по ведению уголовных или гражданских дел), оказанной адвокатами, надо составить:

а) атрибутивный ряд распределения;

б) дискретный ряд распределения;

в) интервальный ряд распределения;

г) вариационный ряд распределения.

2. Какой ряд распределения изображается полигоном?

а) атрибутивный;

б) дискретный;

в) интервальный;

г) вариационный.

3. Интервальный ряд распределения строится тогда, когда признак, положенный в основание группировки является:

а) дискретным с небольшим числом значений;

б) непрерывным;

в) атрибутивным;

г) дискретным с большим числом значений.

4. Максимальное и минимальное значения группировочного признака равны соответственно 28 и 4, число равных по длине интервалов равно 6. Длина интервала группировки равна:

а) 4,1; б) 5,3; в) 5,5; г) 4,0.

5. Ряд распределения магазинов города по числу товарных секции является:

а) атрибутивным;

б) дискретным;

в) интервальным;

г) вариационным.

6. Ряд распределения семей по размеру жилой площади, приходящейся на одного человека, является:

а) атрибутивным;

б) дискретным;

в) интервальным;

г) вариационным.

7. Какой ряд распределения изображается гистограммой?

а) атрибутивный;

б) дискретный;

в) интервальный;

г) вариационный.

8. При построении дискретного ряда распределения, соответствующего данному интервальному ряду распределения, надо в качестве вариант взять:

а) левые границы интервалов;

б) правые границы интервалов;

в) середины интервалов;

г) любые числа из интервалов.

9. Установите соответствие между содержанием и названием рядов распределения.

1) ряд распределения по непрерывному признаку;

2) ряд распределения, по неколичественному признаку;

3) ряд распределения по целочисленному признаку.

а) дискретный ряд;

б) атрибутивный ряд;

в) дискретный ряд;

г) интервальный ряд.