4. Задачи Гидромеханики в бурении
Базовые задачи гидродинамики при промывке и цементировании скважин
При промывке и цементировании скважин базовыми задачами гидромеханики, являются
- задачи о течении жидкости в плоской щели (между двумя бесконечными параллельными пластинами);
- задачи о течении жидкости в круглой трубе и кольцевом пространстве между двумя соосными цилиндрами.
Решение этих задач производятся при следующих условиях:
- жидкость несжимаема
;
течение установившееся
;
все частицы жидкости движутся параллельно
твердым стенкам канала (скважины, трубы),
т.е. одномерное течение вдоль оси канала;
концевые эффекты пренебрежимо малы
т.е. поток в любом сечении идентичен;
вдоль потока действует постоянный
градиент давлений, равный
,
где
- полный перепад давлений между двумя
сечениями, находящимися на расстоянии
L.; на жидкость
действует объемная сила, обусловленная
только силой тяжести:
,
при чем знак (+) – если жидкость движется
вниз, (-) в верх, когда направление оси
OZ совпадает с
направлением движения.
Ниже рассмотрим задачу о течении жидкости в плоской щели (между двумя бесконечными параллельными пластинами).
4.1. Течение в щелевом канале
Ламинарное течение ньютоновской жидкости основными характеристиками потока в щели являются:
- объемный расход 
(4.1)
- средняя скорость 
(4.2)
- коэффициент сопротивления 
. (4.3)
Здесь 2h – ширина щели; b
– глубина щели; L
– высота щели;
- параметр Рейнольдса для плоской щели;
- динамическая вязкость [Па•с];
Например, при
,
,
,
имеем:
;
;
т.е.
на каждые 1000 м гидравлические потери
составят 1,2 МПа.
Ламинарное течение неньютоновской жидкости (Бингама)
Схема профиля скорости в щелевом канале неньютоновской жидкости (Бингама) приведена на Рис. 8. Для неньютоновской жидкости Шведова-Бингама условие страгивания покоящейся жидкости является соотношение:
(4.4)
здесь
- статическое касательное напряжения
сдвига у поверхности канала.
Условием существования движения является соотношение:
(4.5)
здесь
- динамическое касательное напряжения
сдвига;
- жесткое ядро потока.
Для практических инженерных расчетов
представляет интерес случаи, когда
т.е. расчет параметров движущейся
жидкости. Поэтому для неньютоновских
жидкостей основные характеристики
потока имеют вид:
- объемный расход 
(4.6)
- средняя скорость 
(4.7)
- коэффициент сопротивления
(4.8)
из уравнений (4.6, 4.7) можно выразить перепад давлений:
(4.9)
Здесь
- обобщенный параметр Рейнольдса;
- приведенная вязкость жидкости
Шведова-Бингама;
- параметр Сен-Венанна для плоской щели.
Например, при
,
,
,
имеем:
;
;
;
;
т.е.
на каждые 1000 м гидравлические потери
составят 0,675 МПа.
Степенная модель движения неньютоновской жидкости
Соотношения основных характеристик потока имеют вид:
- объемный расход (4.10)
- средняя скорость 
(4.11)
где:
.
- коэффициент сопротивления
(4.12)
Здесь
- обобщенный параметр Рейнольдса;
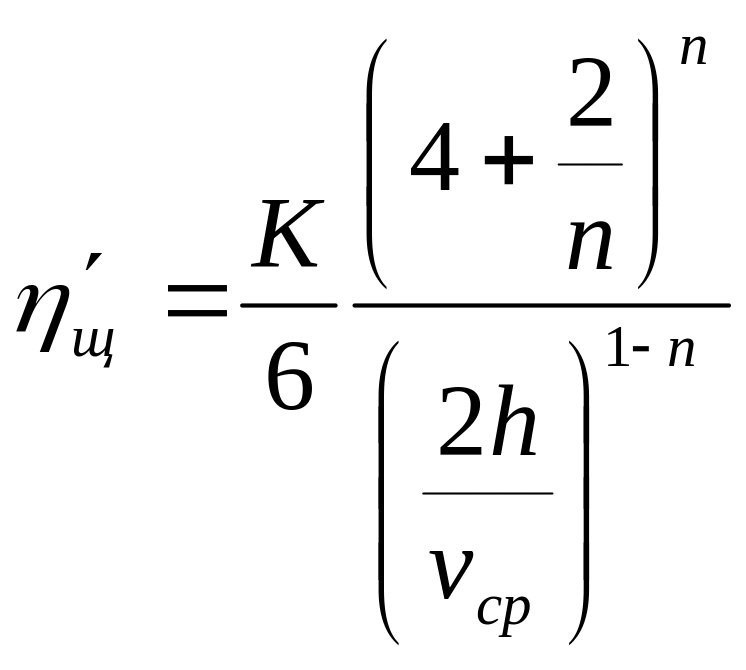- приведенная вязкость Освальда-Вейля
для плоской щели.
Еще раз подтверждает условие, что если n=1, K= , то выражения совпадают с уравнениями для ньютоновской жидкости.
Таким образом, все приведенные формулы
могут быть использованы и при расчете
характеристик течения жидкостей по
наклонной плоскости или длинном лотке
(желобе), у которого ширина b
днища во много раз больше глубины потока
h. Для этого необходимо
принять
и заменить 2b на
b, где
- угол наклона плоскости (лотка) к
горизонту.