5.2. Динамические величины и элементы теории напряжений

Для изучения движения сплошной среды в связи с причинами, которые это движение вызывают, вводят понятие о силах. Силы могут быть внешними и внутренними. Первые являются следствием воздействия на рассматриваемое тело других тел, а вторые возникают в результате взаимодействия элементов данного тела. Силы могут быть двоякого рода: объемные (массовые) поверхностные.

На Рис. 13 приведена схема действия массовых и поверхностных сил в объеме .

Объемная сила действует на массу, заключенную в элементе объема тала, например сила тяжести. Пусть - объемная сила, отнесенная к единице объема. Тогда сила, действующая на бесконечно малый объем равна , а на объем равна .Поверхностная сила действует на элементы, которые можно мысленно выделить внутри тела или на его поверхности. Сила, действующая на бесконечно малый элемент поверхности , равна , где - вектор силы, рассчитанный на единицу площади элемента и приложенный в любой его точке, называется вектором напряжения или просто напряжением.

Напряжение зависит от положения элемента , т.е. от ориентировки его на теле. Если требуется указать, что напряжение относится к площадке с нормалью , то пишут . Проекции напряжений, отнесенные к площадкам, перпендикулярным координатным осям обозначаются через , где - нормальные напряжения; - касательные напряжения, действующие на этих площадках см. Рис. 14. Совокупность 6-ти величин , называют компонентами симметричного тензора напряжений.

Проецируя вектор на направление нормали, получаем нормальное напряжение Рис. 15.

(5.5)

где - направляющая косинусов к нормали.

Касательное напряжение на этой же площадке равно:

(5.6)

где - величина вектора напряжения .

Характерной особенностью напряженного состояния сплошной среды является наличие в каждой точке тела по крайней метре трех взаимно перпендикулярных площадок, на который касательные напряжения равны нулю. Направления нормалей к этим площадкам образуют главные направления. Соответственно напряжения называют главными нормальными напряжениями. Поэтому любое напряженное состояние в рассматриваемой точке может быть вызвано растяжением (сжатием) окрестности точки в трех взаимно перпендикулярных направлениях.

Часто рассматривают приведенное напряжение через интенсивность касательных напряжений:

, (5.7)

- максимальные касательные напряжения.

5.3. Мгновенные уравнения состояния и критерии прочности

Все тела в зависимости от диапазона нагружения и внешних условий в большей или меньшей степени проявляют свойства:

упругость – способности тела накапливать исчезающую при разгрузке деформацию;

пластичность – способности тела накапливать не исчезающую (остаточную) деформацию при разгрузке;

вязкость – способности тела накапливать деформацию во времени при постоянном напряжении или снижать напряжения во времени при постоянной деформации.

Упругость и пластичность относятся к мгновенным свойствам тела, а вязкость к ее временным свойствам.

Обычно для изучения этих свойств и определения состояния тел на грани разрушения проводят простые опыты на образцах - осевое сжатие, растяжение, изгиб, сдвиг, срез и кручение. По результатам опытов устанавливается связь между соответствующими компонентами напряжений, деформаций, и т.д. Определяют параметры предельного состояния, характеризующие разрушения материала. Все это служит основой для выбора определяющих математических моделей деформирования и разрушения твердых тел (горных парод, цементного камня, материала обсадочных и бурильных труд и т.д.).

Рассмотрим характерные мгновенные свойства твердых тел на примере кратковременного осевого растяжения. Общий вид деформационной кривой напряжение-деформация приведен на Рис. 16.

ОА – участок упругих деформаций, где материал подчиняется линейному закону Гука:

(5.8)

E – модуль упругости (модуль Юнга);

АВ – участок пластического течения (или текучести), характеризуемых нарастанием деформации при неизменном напряжении , которое называется пределом упругости или пределом текучести;

ВС – участок упрочнения, где нелинейная зависимость между напряжением и деформацией по аналогии с (5.8) представлена в форме:

(5.9)

- модуль пластичности. Обычно модуль пластичности определяют степенным законом вида:

(5.10)

Здесь K, m – константы материала, полученные при испытаниях на образцах.

СD – участок разрушения, напряжения называется переделом прочности;

LM – участок разгрузки или повторной нагрузки. Характеризуется снятием упругой деформации и сохранением пластической при полной разгрузке. При повторном нагружении выше , материал повышает свой предел упругости . – явление упрочнения. При осевом нагружении цилиндрического образца изменяется и его поперечный размер, определяемый деформацией .

Величина, равная отношению абсолютных значений поперечной деформации к продольной - коэффициент Пуассона:

. (5.11)

Для реальных тел значения коэффициента Пуассона варьируются в интервал: .

Способность твердых тел сжиматься (уплотнятся) или расширятся (разуплотнятся) устанавливается диаграммой всестороннего давления–объемная деформация и в широком диапазоне характеризуется выражением вида:

. (5.12)

Здесь - модуль объемного сжатия или расширения в зависимости от вида нагружения.

Связь модуля и коэффициента Пуассона выражается как:

. (5.13)

Классификация горных пород

По полученной деформационной кривой находят основные механические параметры тела, устанавливают меру пластичности.

Возможные виды деформационных кривых и соответствующие им формы разрушений для горных пород приведены на Рис 17.

1 – очень хрупкая, деформация до внезапного разрыва, характеризуемого образование трещин отрыва перпендикулярно к наименьшему главному напряжению. Накопленная при этом деформация не превышает 1%;

2 – хрупкая, наблюдается малая пластическая деформация до разрыва и образуются трещины отрыва и скола. Накопленная при этом деформация не превышает 1-5%;

3 – умеренно хрупкая, поведение промежуточное между хрупким и текучим, пик обозначает нарушение целостности без общей потере связности. Разрушение происходит в результате образования трещин скола. Накопленная при этом деформация не превышает 2-8%;

4 – умерено пластическая. Разрушение сопровождается рассеянной деформацией. Накопленная при этом деформация не превышает 5-10;

5 – идеально пластическая, хорошо выражен предел текучести, сменяющийся однородным течением. Деформация до разрыва более 10%;

6 – пластическая с упрочнением, предел текучести слабо выражен, процесс сопровождается работой упрочнения. Деформация до разрыва более 10%.

Принадлежность горной пароды к одному из приведенных типов определяет расчетную математическую модель и предельное состояние.

Характеристики предельного состояния

Для простого одноосного нагруженного состояния (чистое сжатие, растяжение) в инженерной практике предельное значение определяют от среднего нормального напряжения , предложенная Э. Хоеком:

(5.14)

Здесь – значение при . – константы, являющиеся функциями температуры, влажности.

Разновидностью выражения (5.14) является зависимость Д. Франклина при : . При уравнение преобразуется в лилейную аппроксимацию, называемую критерием Мора:

. (5.15)

Примером влияния влажности на механическую прочность пород может служить понтическая глина. Согласно экспериментальным данным применение (5.15) вполне приемлема до давления , при этом значения для соответствующей влажности следующие:

	2	5	11	13
	10	7	5	3
	1.4	1.26	0.5	0

При сложнонапряженном состоянии упругое деформирование изотропных тел описывается уравнениями состояния, называемыми обобщенным законом Гука:

В напряжениях:

(5.16)

В деформациях:

(5.17)

Здесь - модуль сдвига; - коэффициент Ламе.

На основании уравнений (5.12) и формул (5.4) и (5.7) выведено полезное соотношение:

(5.18)

откуда видно, что интенсивность касательных напряжений пропорциональна интенсивности деформации сдвига .

Критерии прочности

Условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения – критерий прочности при кратковременном нагружении.

При одноосном напряженном состоянии критерий прочности оценивается предельным значением напряжения (см. выше 5.14);

При переходе к сложному состоянию критерий прочности в общем случае определяется некоторой поверхностью:

(5.19)

Здесь – интенсивность касательный напряжений; - среднее нормальное напряжение; - параметр Лоде-Надаи, изменяется в пределах от (-1 до+1) и указывает на взаимоотношения главных нормальных напряжений.

В инженерных расчетах применяют выражения вида:

(5.20)

Здесь вид функции правой части определяют экспериментально для конкретных материалов. В частности при следует критерий Губера- Мизеса, основанный на гипотезе, что процесс разрушения зависит главным образом от изменения формы элемента тела:

(5.21)

При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считая любое из направлений в этих плоскостях эквивалентными в отношении механических свойств.

Такие тела принято называть транверсально-изотропными. Рассмотрим упругие постоянные некоторых горных пород, заимствованы из разных литературных источников Рис. 18. Здесь - модули Юнга по направлениям, параллельным и перпендикулярным напластованию; - коэффициенты Пуассона, характеризующие поперечное сжатие в плоскости напластования при сжатии в той же плоскости и в направлении перпендикулярном к ней.

Для большинства горных пород модули сдвига рекомендуется вычислять по формулам:

, , (5.22)

где - основной параметр анизотропии.

Так как прочность горных пород на сжатие существенно отличается от прочности на растяжение или сдвиг, как по значению, так и по направлению, то в случае, когда необходимо учесть воздействия происходящих в направлениях, отличающихся от направлений плоскостей напластования (параллельных и перпендикулярных) применяется обобщенные критерии анизотропных тел.

К таким критериям можно отнести обобщения критерия Мора по главным направлениям:

. (5.23)

Буквенные обозначения являются коэффициентами, характеризующие отношения между критериями прочности на растяжения и сжатие плоскости напластования и перпендикулярной к ней.

Уравнения состояния с учетом порового давления

Наиболее полное изучение механических свойств горных пород, учитывающее влияние порового (пластового) давления, осуществляется путем трехосного компрессионного испытания, принципиальная схема которого приведена на. Рис.19 а.

Цилиндрический образец d=10-30 мм и высотой l=(2-3)d упаковывают в непроницаемую оболочку и помещают в специальную толстостенную стальную камеру, где поддерживается всестороннее давление и температура. Поровое давление p_п поддерживают постоянным волюмометром. Деформация образца производится за счет винтового поршня.

В испытаниях на сжатие или растяжение дифференциальное давление накладывается на гидростатическое , поэтому напряженное состояние в каждой точке образца определяется тремя главными компонентами Рис.19 б:

, (5.24)

В результате экспериментов было определена поправка, характеризующая учет порового давления в горном пласте. С учетом этой поправки закон Гука (5.17) и критерий прочности (5.20) примут вид:

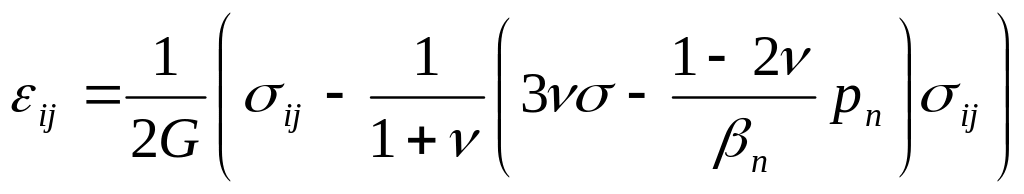(5.25)

, (5.26)

Здесь - коэффициент порового давления, характеризующий различную сопротивляемость скелета породы расширению и сжатию. - модули объемной деформации расширения и сжатия. Установлено так же, что изменения формы элемента тела не зависит от порового давления.

Для глин и глинистых пород, склонных к набуханию, компоненты деформации в уравнении (5.25) необходимо дополнить слагаемыми:

, . (5.27)

Здесь - коэффициенты объемного расширения при увлажнении породы и при ее нагревании; - текущая и начальная влажность породы; - текущая и начальная температура породы.