4.6. Гидравлический удар в скважине

Установившееся (стационарное) течение жидкости в скважине сопровождается, как правило, переходными нестационарными эффектами, связанными либо с технологическими приемами управления при промывке или цементировании, либо с осложнениями при бурении скважин.

В этом случае возникает так называемое явление гидравлического удара, характеризуемое заметным ростом или падением давления в циркуляционной системе. С точки зрения гидравлических расчетов представляют интерес задачи связанные с быстро протекающими нестационарными процессами, когда изменение скорости жидкости в каком-либо сечения потока происходит за время, соизмеримое со временем прохождения звуковой волны в заполненной жидкостью трубе.

Практическими примерами этих задач служат: внезапная разгерметизация обсадной колонны после прессовки; создание скачка давления для вызова притока или гидроразрыва пласта; распределение по длине скачка давлений.

Рассмотрим одну из основных задач - определение максимального изменения давления в заданном сечении трубы, в частности в местах соединения труб с различными диаметрами. На Рис. 12 приведена расчетная схема последовательного соединения неоднородных труб.

Здесь S – площадь проходного сечения; L – длина участков труб; a - диссипативный параметр для ньютоновской жидкости: ; - гидравлический радиус ; с -скорость звука в жидкости, текущей по трубе с упругими стенками ; K – приведенный модуль объемного сжатия, учитывающий упругость как жидкости, так и стенок трубы

(4.47)

где - модуль объемного сжатия жидкости; - модуль упругости материала стенок трубы; - безразмерный коэффициент, зависящий от формы сечения и толщины стенок трубы.

Согласно результатам следований для глинистого раствора плотностью от 1600 до 1950 кг/м³ при давлении от 3 до 60 МПа коэффициент сжимаемости . Для цементного раствора плотностью 1800 кг/м³ в том же диапазоне изменения давлений . Модуль упругости горных пород может быть того же порядка или на порядок выше. Модуль упругости для материала стальных труб выше на два порядка .

Безразмерный коэффициент для круглой тонкостенной трубы : (4.48)

для толстостенной трубы:

(4.49)

где - внутренний диаметр; - толщина стенки трубы; - коэффициент Пуассона материала трубы.

Значение максимального давления в сечении перехода определится:

(4.50)

где .

Эта формула может быть использована для вычисления давления последовательно в других узловых сечениях, если вместо величины подставлять скачек давления, определенный в предыдущем узле. Например, за сечением получим:

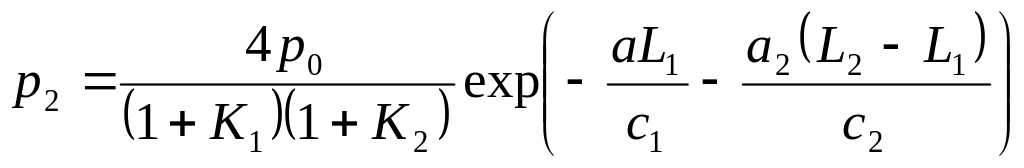(4.51)

где , - площадь поперечного сечения и скорость звука в третьем участке трубопровода.

4.7. Отчистка ствола скважины от шлама

Одна из основных функций борового раствора при бурении скважин – обеспечение выноса на дневную поверхность разрушенной на забое и осыпающейся со стенок породы (шлама). При этом качество очистки ствола скважины достигается надлежащим выбором режима промывки и свойств бурового раствора.

В настоящее время теоретическое решение этой задачи состоит в определении средней скорости потока в затрубном пространстве из условия гидротранспорта шлама:

(4.52)

где - скорость осаждения частицы шлама характерного размера , относительно несущей ее жидкости.

Условие (4.52) не гарантирует качество очистки, так как не является достаточным критерием. Это объясняется сложным характером движения частиц твердого тела в потоке жидкости и зависимостью этого движения от многих факторов. Гарантировать полный вынос шлама, поступающего в затрубное пространство, можно, если выполняется неравенство:

(4.53)

где - скорость жидкости в точке расположения центра частицы, определяемого координатой . Это возможно лишь при одном условии, когда каждая из частиц шлама расположена внутри яра выноса.

Однако опыты свидетельствуют о том, что 100 % выноса шлама на поверхность не бывает. Соответственно частицы шлама могут занимать положения вне ядра выноса. Для течения жидкости Шведова-Бингама вероятность выноса любой частицы шлама размером , внесенной в затрубное пространство, будет равна:

. (4.54)

Здесь - параметр Сен-Венана для кольцевого сечения. Следовательно, ненулевая вероятность выноса возможна при средней скорости:

(4.55)