Спектр сигнала с угловой модуляцией при малых индексах модуляции

При т << 1 можно положить и пренебречь значениями функций Бесселя более высоких порядков. Тогда выражение (11) принимает вид

(13)

Таким образом, при т << 1 в спектре сигнала с угловой модуляцией содержатся несущее колебание и две боковые состав­ляющие, верхняя и нижняя, на частотах и . Индекс "т" здесь играет такую же роль, как коэффициент амплитудной модуляции "М". Имеется также и существенное различие спектров AM - сигналов и колебаний с угловой модуляцией, состоящее в том, что нижнее боковое колебание во втором случае имеет дополнительный фазовый сдвиг на 180⁰ .

Радиосигналы с линейной частотной модуляцией

При линейной частотной модуляции (ЛЧМ) мгновенную частоту заполнения можно определить выражением при , где скорость линейного изменения частоты. Поэтому мгновенное значение такого колебания можно представить в виде

.

Характерный вид импуль­са с ЛЧМ и закон изменения частоты приведены на рис 2.

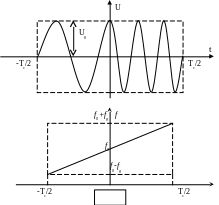
Рисунок 2.

Произведение полной девиации частоты на дли­тельность импульса является основным параметром сиг­нала и называется "базой сигнала";

(14)

С учетом (14) ЛЧМ - сигнал определяется выражени­ем:

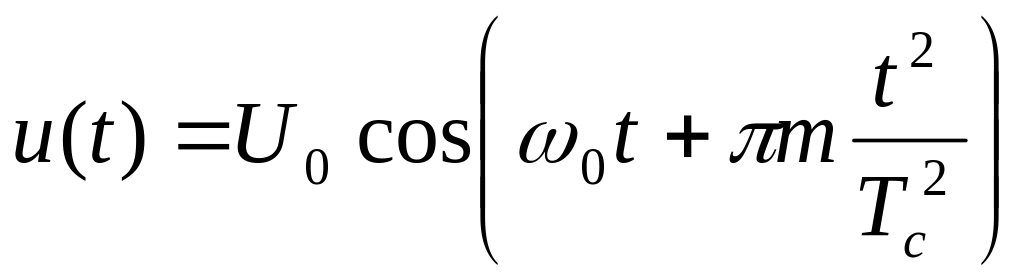
Анализ выражения спектральной плотности ЛЧМ - сигнала [1-2] показывает, что при больших значениях "m" форма кривой модуля спектральной плотности при­ближается к прямоугольной, а шири­на спектра - к величине "2Wg", при этом фазовая характеристика прини­мает вид квадратичной параболы. Гра­фики модуля спектральной плотнос­ти (1) и фазовой характеристики (2) ЛЧМ - сигнала приведены на рис. 3.

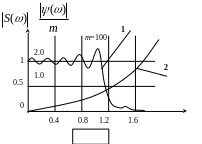
Рисунок 3.

ЛЧМ - сигналы с большой базой ( ) представляют большой практический интерес для современной радиотехники в плане их обнаружения на фоне помех после корреляционной обработки. Дело в том, что огибающая корреля­ционной функции ЛЧМ - импульса

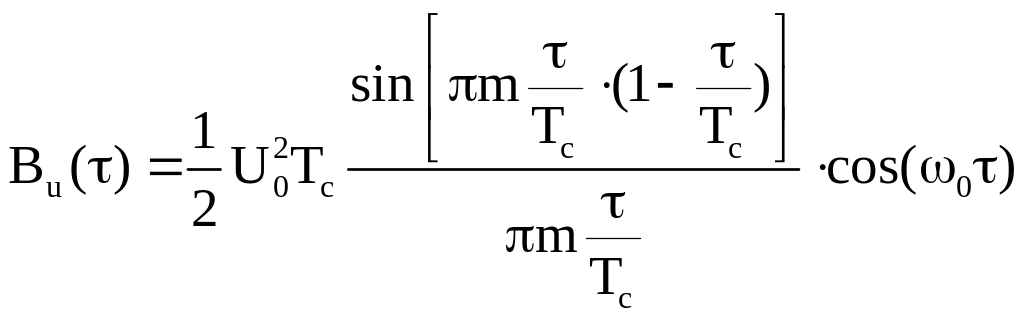
образует весьма острый пик, который легко выделяется поро­говыми устройствами, а частота заполнения постоянна и равна .

Фазовая и частотная манипуляции

В системах передачи дискретной информации сигнал сообще­ния s(t) обычно принимает одно из двух возможных значений 0 или 1 двоичного (бинарного) кода. Поэтому гармоническая несу­щая, модулированная таким сигналом по фазе или частоте, называется, соответственно, фазовой (ФТ) или частотной (ЧТ) телеграфией. В системе, работающей с ЧТ, символу "1" соответ­ствует излучение колебания с частотой , а символу "0" - колебание с частотой . Эта система с активной паузой (непрерывное излучение). В системе, работающей с ФТ, символу "0" соответствует колебание частоты с начальной фазой . Символу "1" - колебание с той же частотой , но с другой

начальной фазой . Чаще всего выбирают . Система с ФТ имеет также активную паузу.

Спектральный состав фт сигнала

Спектр ФТ - сигнала можно получить, используя выражения для спектра АТ - сигнала (см. метод указания к лабораторной работе "Исследование спектров АМ - сигналов").

Полагая, что фаза сигнала ФТ в процессе манипуляции меня­ется на 180⁰ , необходимый нам сигнал можно получить из сигнала AT вычитанием гармонического колебания, синфазного с одной из двух посылок ФТ - сигнала (рис. 4).

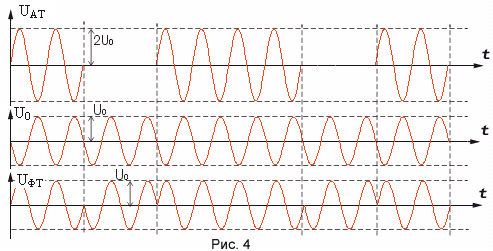
Рисунок 4.

Поэтому любой сигнал ФТ

,

где s(t) принимает значение "0" или "1" в соответствии с передаваемой информацией, может быть представлен в виде

Тогда спектральный состав фазоманипулированного сигнала определится следующим выражением:

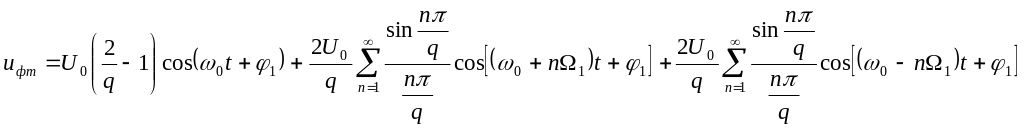
Сравнивая полученное выражение с выражением спектра АТ - сигнала, можно сделать вывод, что спектр сигнала ФТ отличается от спектра АТ - сигнала амплитудой несущего колебания (на часто­те ) и увеличенными в 2 раза амплитудами боковых полос. Последний факт объясняется тем, что ФТ представляет собой систему с активной паузой, т. е., в отличие от AT, излучение идет непрерывно, поэтому средняя мощность увеличивается.