Лабораторная работа №4 исследование спектров сигналов с угловой модуляцией

Цель работы: изучение спектров сигналов с частотной и фазовой модуляцией при изменении их основных параметров.

Краткие теоретические сведения к выполнению лабораторной работы

Модулированные радиосигналы, у которых в несущем гармо­ническом колебании передаваемое сообщение S(t) изменяет полную фазу (t) при U₀ = const, получили название сигналов с угловой модуляцией.

В зависимости от того, какая из компонент полной фазы подвергается изменению, частота или начальная фаза различают, соответственно, частотную и фазовую модуляции.

Пусть полная фаза (t) связана с модулирующим сигналом S(t) следующей зависимостью:

(1)

где K_фм — некоторый коэффициент пропорциональности,

- значение частоты при отсутствии полезного сигнала, т.е. при s(t) = 0.

Таким образом, зависимость (1) реализует фазовую модуляцию (ФМ):

(2)

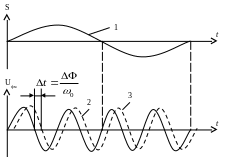
Рисунок 1.

Если s(t) = 0, то ФМ - колебание является простым гармони­ческим. С увеличением сигнала s(t) полная фаза (t) растет быстрее, чем по линейному закону . При уменьшении s(t)происходит спад скорости роста (t) во времени.

На рис. 1 изображен пример ФМ - сигнала (цифрами обозначено: 1— моду­лирующий сигнал, 2 — несущее колебание, 3 — фазо –модулированное колебание).

В моменты времени, когда s(t) достигает экстремальных значений, абсолютная величина фазового сдвига между ФМ - сигналом и немодулированным гармоническим колебанием ока­зывается наибольшей. Предельное значение фазового сдвига называют девиацией фазы .

Мгновенная частота сигнала с угловой модуляцией опре­деляется как производная от полной фазы (t) по времени:

(3)

Тогда:

(4)

Если между модулирующим сигналом s(t) и существует связь вида

(5)

то имеет место частотная модуляция сигнала, поэтому

.

В моменты времени, когда s(t) достигает экстремальных значений, абсолютная величина отклонения от величины оказывается наибольшей. Предельное значение этого отклонения частоты называют девиацией частоты

Если модулирующий сигнал s(t) - достаточно гладкая функ­ция времени, то внешних различий между осциллограммами ФМ и ЧМ - сигналов (при однотональной модуляции) нет. Однако между ними есть принципиальная разница: фазовый сдвиг ФМ - сигнала по отношению к немодулированному несущему колеба­нию пропорционален s(t), в то время как для ЧМ - сигнала этот сдвиг пропорционален интегралу от передаваемого сообщения s(t).

Однотональные сигналы с угловой модуляцией

В случае однотонального ЧМ - сигнала мгновенная частота в соответствии с формулой (5) представляется в виде

(6)

где - девиация частоты сигнала.

На основании выражения (4) полная фаза такого сигнала

(7)

Величина называется индексом однотональной частотной модуляции и отображает девиацию фазы сигнала (в радианах).

В дальнейшем для простоты положим , тогда мгно­венное значение ЧМ - сигнала запишется:

(8)

Аналитическая форма записи однотонального ФМ – сигнала имеет вид

(9)

где имеет смысл девиации фазы.

Несмотря на кажущееся сходство выражений (8) и (9), следует иметь в виду, что ЧМ - и ФМ - сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды модулирующего сигнала [1]. При частотной модуляции величина девиации частоты пропорциональна амплитуде модулирующего сигнала s(t) и не зависит от его частоты. В случае же фазовой модуляции пропорциональным амплитуде модулирующего сигнала оказывается ее индекс , который также не зависит от частоты [2].

Вследствие этого девиация частоты при ФМ линейно увеличива­ется с ростом частоты.