Лабораторна робота № 3.2 Визначення опору провідників за допомогою містка Уітстона

Мета роботи: 1) визначити опори провідників; 2) перевірити справедливість законів послідовного і паралельного сполучення опорів.

Теоретичні відомості

(Теорія до даної роботи описана в конспекті лекцій §3.10-3.12)

Опір провідника є важливою його характеристикою. З природою електричного опору і його залежністю від температури можна ознайомитися в теоретичних відомостях до роботи № 3.4.

В даній роботі використовується досить точний метод вимірювання електричного опору за допомогою містка Уітстона, теорія якого ґрунтується на законах Кірхгофа (див. теоретичні відомості до роботи 3.3).

Розглянемо схему містка Уітстона (рис.1). На рис.1 – реохорд; – магазин опорів; – невідомий опір; – додатковий змінний опір, який обмежує струм через гальванометр ; , і – ключі.

Р

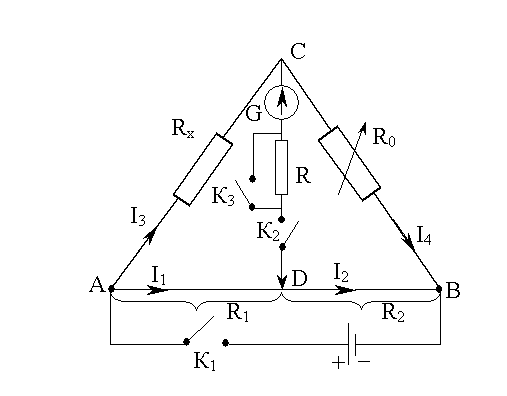Рис.1

еохорд – це дротина однакового поперечного перерізу, вздовж якої розміщена лінійна шкала. По реохорду може переміщуватися повзунок, за допомогою якого забезпечується ковзний контакт в точці D.

Переміщуючи повзунок по реохорду, можна добитися такого положення, при якому струм через гальванометр відсутній (місток збалансований). В цьому випадку потенціали точок С і D однакові, тобто , , де через позначено різниці потенціалів між відповідними точками. Але , , , . Тоді будемо мати

, (1)

. (2)

Для випадку балансу містка , . Поділимо почленно (1) на (2)

, (3)

звідки

. (4)

Оскільки дротина АВ однорідна і однакового поперечного перерізу, то відношення опорів можна замінити відношенням довжин дротин i . Тоді в (4) маємо

або

, (5)

де . Співвідношення (5) використовується як робоча формула для визначення опору .

З формули (5) видно, що при даному баланс містка може бути при різних і . Однак розрахунок показує, що точність вимірювання буде найбільшою тоді, коли відношення близьке до одиниці. Дійсно, відносна похибка дорівнює

. (6)

Розглядаючи як функцію від і досліджуючи цю функцію на екстремум при незмінних величинах , , можна показати, що відносна похибка має мінімум при .

Хід роботи

1. Скласти схему згідно рис.1.

2. Ввімкнути опір – розімкнути ключ .

3. Встановити ковзний контакт на середині реохорда.

4. Замкнути ключ .

5. Замикаючи ключ на короткий проміжок часу і змінюючи опір , добитися грубого балансу містка.

6. Вимкнути опір (замкнути ключ ) і, змінюючи опір , добитися точного балансу містка. Якщо цього не вдається досягти зміною опору , то можна в невеликих межах змінювати положення ковзного контакту реохорда. При збалансованому містку записати , і у таблицю.

7. Не змінюючи положення ковзного контакту, зміною опору розбалансувати міст і знову його збалансувати. Записати нове значення . Таким чином вимірювання повторити не менше трьох разів.

8. Вимірювання провести для двох невідомих опорів окремо, їх послідовного і паралельного з’єднань.

9. Обчислити опори за формулою (5).

10. Відносну похибку (для одного з опорів) можна розрахувати за формулою (6); тоді абсолютна похибка .

11. Користуючись величинами визначених опорів, перевірити закони послідовного і паралельного сполучення опорів. Зробити висновок.

Таблиця вимірювань

.

Опір	№ з/п
І	1.
	2.
	3.
	Ср.
ІІ	1.
	2.
	3.
	Ср.
І і ІІ послідовно	1.
	2.
	3.
	Ср.
І і ІІ паралельно	1.
	2.
	3.
	Ср.