2. Условие устойчивости оу.

Воспользуемся критерием устойчивости [ ], широко используемым в теории автоматического управления.

Усилитель является устойчивым если сдвиг фазы выходного сигнала возвратного отношения Τ(jω) в области частот, где модуль |Τ(jω)|>1 не превышает -135˚ (с учётом минимального запаса по фазе Δφ=45˚)

Если сдвиг фазы выходного сигнала не превышает -135˚, то |Τ(jω)| может быть больше единицы.

Ответим на вопрос, какая форма АЧХ ОУ соответствует сформулированному условию устойчивости. Наиболее часто используется следующая форма возвратного отношения.

Τ(jω)= , (5.1)

где , - постоянные времени, определяющие полюса в передаточной характеристике ОУ.

форма |Τ(jω)| представлена на рис 5.1.

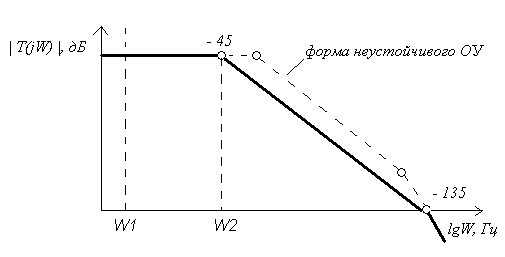
рис 5.1

Из рис 5.1 следует, что на частоте запас по фазе Δφ=45˚ , а на частоте запас по фазе Δφ= -135˚, т.е. форма диаграммы |Τ(jω)| соответствует условию устойчивой работы.

Возвратное отношение Τ(jω) связано следующим соотношением с коэффициентом усиления ОУ при разомкнутой ОС.

, (5.2)

где - коэффициент усиления ОУ с разомкнутой цепью отрицательной ОС,

- коэффициент передачи по цепи обратной связи,

- коэффициент передачи ОУ с замкнутой цепью ОС.

Таким образом, целью коррекции ФЧХ является получение формы частотной характеристики возвратного отношения, показанной на рис 5.1.

Рассмотрим зависимость коэффициента усиления от частоты трёхкаскадного ОУ.

, (5.3)

где - коэффициент усиления ОУ с разомкнутой цепью ОС по постоянному току.

Построим асимптотические диаграммы (диаграммы Боде) модуля и фазы коэффициента .

Считаем, что цепи обратной связи имеют активный характер, т.е. не зависит от частоты.

Определим максимально возможную по условию устойчивости величину модуля возвратного отношения.

Из рис 5.2 видно, что фаза Τ(jω) совпадает с фазой , а для модуля коэффициента усиления справедливо следующее соотношение:

(5.4)

или (5.5)

рис 5.2

Из графика на рис 5.2 видно, что сдвиг фазы φ=-135˚

на частоте . По условию устойчивости ( )при этом

|Τ(jω)|=1 , что соответствует границе устойчивости работы, т.е. на графике в логарифмическом масштабе этому условию соответствует горизонтальная линия 80 дБ. На низких частотах максимально возможная величина |Τ(jω)|=20дБ, а минимальная величина . При увеличении глубины ОС (т.е. увеличения сдвиг фазы превышает -135˚ и ОУ возбуждается.

Таким образом, целью коррекции частотно-фазовых характеристик ОУ является придание такой формы диаграммы Боде для АЧХ, при которой сдвиг по фазе коэффициента передачи с замкнутой цепью ОС не превышал бы -135˚ .

Реализация цели осуществляется с помощью реактивных RC-цепей.

3. Коррекция чфх интегрирующего типа.

На рис 5.3 представлена цепь коррекции интегрирующего тока.

рис 5.3

Здесь R₁ и С – элементы, подключаемые к соответствующим внешним клеммам.

Ri – внутреннее сопротивление ОУ в точке подключения цепи коррекции.

Частотно-фазовая характеристика интегрирующего корректирующего фильтра имеет вид

, (5.6)

где ; ;

на частотах f > f₄

,

где - максимальное затухание фильтра (рис 5.4)

рис 5.4

рис 5.5

рис 5.6

Предположим, что интегрирующий фильтр включён в цепь усилителя с характеристикой (5.6). Тогда возвратное отношение будет иметь вид:

(5.7)

Для уменьшения числа полюсов выберем ,

При этом

_, (5.8)

Нарисуем график результирующей передаточной характеристики и учтём, что . Из графика найдём

(5.9)

Запишем (5.9) в линейных единицах измерения

, отсюда .

Таким образом, зная , можно определить величину . По найдём величины элементов коррекции С и R₁.

; ; .

Пример.

Для примера взят ОУ1УТ531.

, , ,

, .

Необходимо определить и , обеспечивающие устойчивую работу ОУ при .

Решение:

Т.е. устойчивость ОУ с корректирующим интегральным фильтром достигается за счёт сдвига характеристик в область более низких частот.